[人工智能]深度学习入门（三）多层感知机

前言

因为工作需求需要接触到深度学习知识，导师推荐了一本书用来入门：《动手学深度学习（PyTorch版）》

在此处记录一下学习内容以及学习总结，文章以原作者书籍为基础，插入一些自己的总结与心得做参考（高亮部分），喜欢阅读原文的可以访问原文链接：动手学深度学习(PyTorch版)

了解完单层神经网络后，这一节主要学习多层神经网络模型：多层感知机

上一节文章链接：深度学习入门（二）Softmax回归模型

多层感知机

我们已经介绍了包括线性回归和softmax回归在内的单层神经网络。然而深度学习主要关注多层模型。在本节中，我们将以多层感知机（multilayer perceptron，MLP）为例，介绍多层神经网络的概念。

1. 隐藏层

多层感知机在单层神经网络的基础上引入了一到多个隐藏层（hidden layer）。隐藏层位于输入层和输出层之间。图3.3展示了一个多层感知机的神经网络图，它含有一个隐藏层，该层中有5个隐藏单元。

在图3.3所示的多层感知机中，输入和输出个数分别为4和3，中间的隐藏层中包含了5个隐藏单元（hidden unit）。由于输入层不涉及计算，图3.3中的多层感知机的层数为2。由图3.3可见，隐藏层中的神经元和输入层中各个输入完全连接，输出层中的神经元和隐藏层中的各个神经元也完全连接。因此，多层感知机中的隐藏层和输出层都是全连接层。

前两节的单层网络只有输出层进行了计算，而在多层感知机里面，则多了一层隐藏层进行计算，同时与之前的单层网络一样，多层感知机的每一层也都是全连接层

具体来说，给定一个小批量样本$\mathbf{X}\in {\mathbb{R}}^{n\times d}$，其批量大小为$n$，输入个数为$d$。假设多层感知机只有一个隐藏层，其中隐藏单元个数为$h$。记隐藏层的输出（也称为隐藏层变量或隐藏变量）为$\mathbf{H}$，有$\mathbf{H}\in {\mathbb{R}}^{n\times h}$。因为隐藏层和输出层均是全连接层，可以设隐藏层的权重参数和偏差参数分别为${\mathbf{W}}_h\in {\mathbb{R}}^{d\times h}$和 ${\mathbf{b}}_h\in {\mathbb{R}}^{1\times h}$，输出层的权重和偏差参数分别为${\mathbf{W}}_o\in {\mathbb{R}}^{h\times q}$和${\mathbf{b}}_o\in {\mathbb{R}}^{1\times q}$。

我们先来看一种含单隐藏层的多层感知机的设计。其输出$\mathbf{O}\in {\mathbb{R}}^{n\times q}$的计算为

$$\begin{array}{rl}\mathbf{H}& =\mathbf{X}{\mathbf{W}}_h+{\mathbf{b}}_h,\\ \mathbf{O}& =\mathbf{H}{\mathbf{W}}_o+{\mathbf{b}}_o,\end{array}$$

也就是将隐藏层的输出直接作为输出层的输入。如果将以上两个式子联立起来，可以得到

$$\mathbf{O}=(\mathbf{X}{\mathbf{W}}_h+{\mathbf{b}}_h){\mathbf{W}}_o+{\mathbf{b}}_o=\mathbf{X}{\mathbf{W}}_h{\mathbf{W}}_o+{\mathbf{b}}_h{\mathbf{W}}_o+{\mathbf{b}}_o.$$

从联立后的式子可以看出，虽然神经网络引入了隐藏层，却依然等价于一个单层神经网络：其中输出层权重参数为${\mathbf{W}}_h{\mathbf{W}}_o$，偏差参数为${\mathbf{b}}_h{\mathbf{W}}_o+{\mathbf{b}}_o$。不难发现，即便再添加更多的隐藏层，以上设计依然只能与仅含输出层的单层神经网络等价。

按照上面的解释多层感知机的各个层之间本质上相当于一个单层网络，计算时直接将相邻的两层作为单层网络的输入与输出，最后联立起来，得到最终的输入与输出的关系，但这样的输出关系实际上还是和单层神经网络等价，但我们要的是多层神经网络，所以单纯的联立肯定不对，需要进行一些其他处理，因此引入激活函数

2. 激活函数

上述问题的根源在于全连接层只是对数据做仿射变换（affine transformation），而多个仿射变换的叠加仍然是一个仿射变换。解决问题的一个方法是引入非线性变换，例如对隐藏变量使用按元素运算的非线性函数进行变换，然后再作为下一个全连接层的输入。这个非线性函数被称为激活函数（activation function）。下面我们介绍几个常用的激活函数。

仿射变换，又称仿射映射，是指在几何中，一个向量空间进行一次线性变换并接上一个平移，变换为另一个向量空间

因为全连接层的仿射变换主要还是线性变化，对于y=ax+b 这样的函数，当x的输入很大时，y的输出也是无限大小的，经过多层网络叠加后，值更加起飞了，而在大多数情况下，我们需要的输出是一个概率，这显然不符合我们的期望，同时线性变化的表达能力有限，有许多复杂关系无法表示，但如果引入非线性变换，就可以增加整体模型的表达能力

2.1 ReLU函数

ReLU（rectified linear unit）函数提供了一个很简单的非线性变换。给定元素$x$，该函数定义为

$$\text{ReLU}(x)=\max (x,0).$$

可以看出，ReLU函数只保留正数元素，并将负数元素清零。为了直观地观察这一非线性变换，我们先定义一个绘图函数xyplot。

%matplotlib inline
import torch
import numpy as np
import matplotlib.pylab as plt
import sys
sys.path.append("..") 
import d2lzh_pytorch as d2l

def xyplot(x_vals, y_vals, name):
    d2l.set_figsize(figsize=(5, 2.5))
    d2l.plt.plot(x_vals.detach().numpy(), y_vals.detach().numpy())
    d2l.plt.xlabel('x')
    d2l.plt.ylabel(name + '(x)')

我们接下来通过Tensor提供的relu函数来绘制ReLU函数。可以看到，该激活函数是一个两段线性函数。

x = torch.arange(-8.0, 8.0, 0.1, requires_grad=True)
y = x.relu()
xyplot(x, y, 'relu')

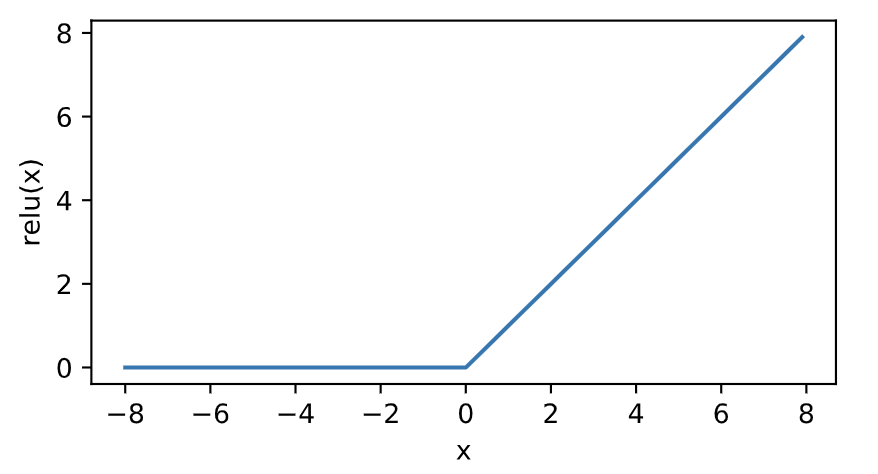
显然，当输入为负数时，ReLU函数的导数为0；当输入为正数时，ReLU函数的导数为1。尽管输入为0时ReLU函数不可导，但是我们可以取此处的导数为0。下面绘制ReLU函数的导数。

y.sum().backward()
xyplot(x, x.grad, 'grad of relu')

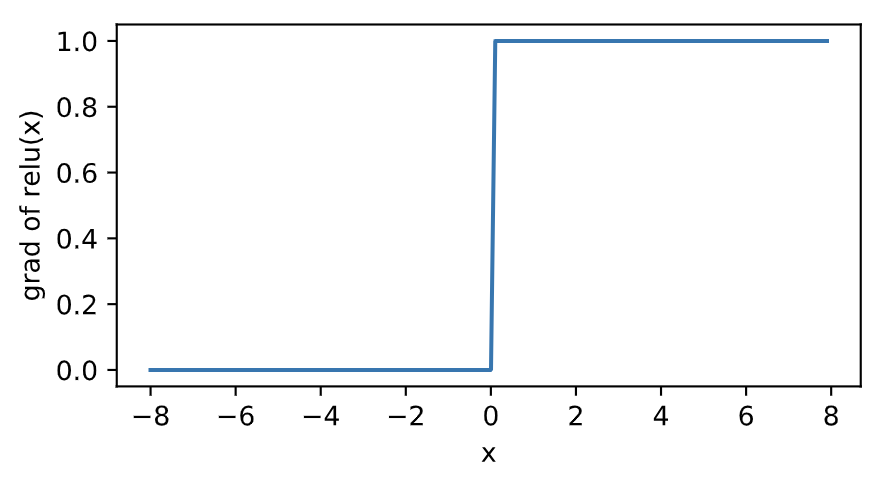
Relu函数输入数值小于0时输出为0，导数可以看成0；输入大于0时输出为输入，导数为1，该函数计算简单，运算量小

2.2 sigmoid函数

sigmoid函数可以将元素的值变换到0和1之间：

$$\text{sigmoid}(x)=\frac{1}{1+\exp (?x)}.$$

sigmoid函数在早期的神经网络中较为普遍，但它目前逐渐被更简单的ReLU函数取代。在后面“循环神经网络”一章中我们会介绍如何利用它值域在0到1之间这一特性来控制信息在神经网络中的流动。下面绘制了sigmoid函数。当输入接近0时，sigmoid函数接近线性变换。

y = x.sigmoid()
xyplot(x, y, 'sigmoid')

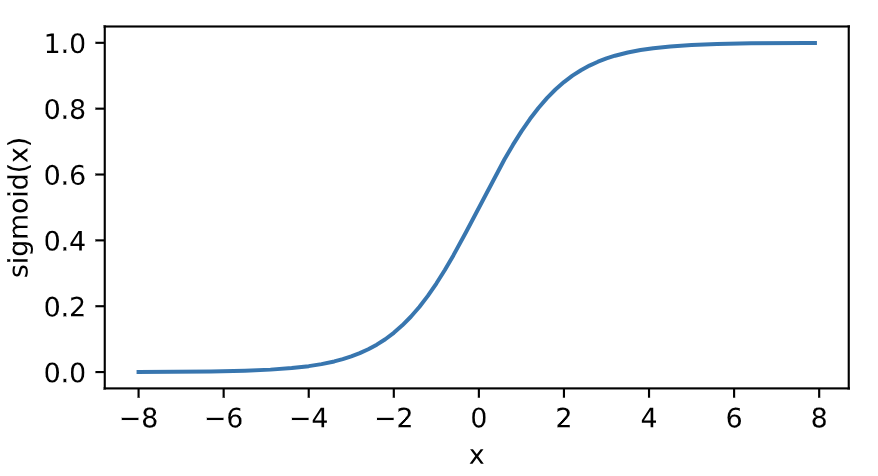
依据链式法则，sigmoid函数的导数

$${\text{sigmoid}}^{\prime }(x)=\text{sigmoid}(x)\left(1?\text{sigmoid}(x)\right).$$

下面绘制了sigmoid函数的导数。当输入为0时，sigmoid函数的导数达到最大值0.25；当输入越偏离0时，sigmoid函数的导数越接近0。

x.grad.zero_()
y.sum().backward()
xyplot(x, x.grad, 'grad of sigmoid')

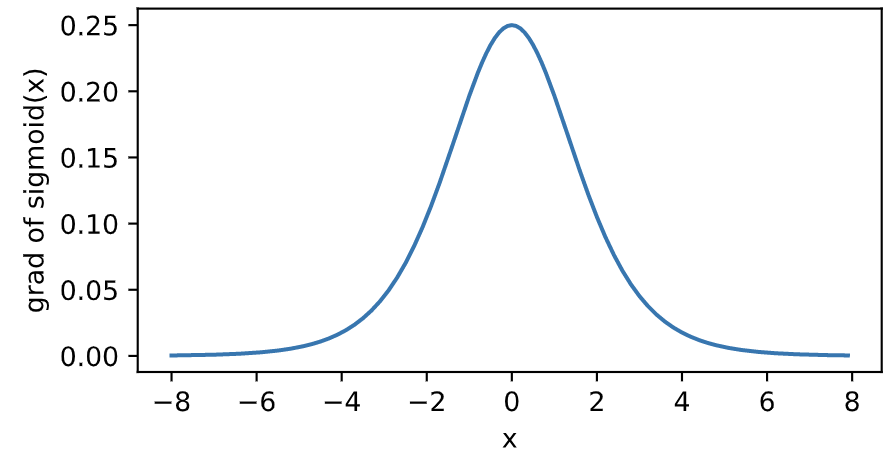
sigmoid激活函数能够把输入的连续实值变换为0和1之间的输出，并且如果输入是非常大的负数，那么输出就是0；如果是非常大的正数，那输出就是1，该函数运算量较大

2.3 tanh函数

tanh（双曲正切）函数可以将元素的值变换到-1和1之间：

$$\text{tanh}(x)=\frac{1?\exp (?2x)}{1+\exp (?2x)}.$$

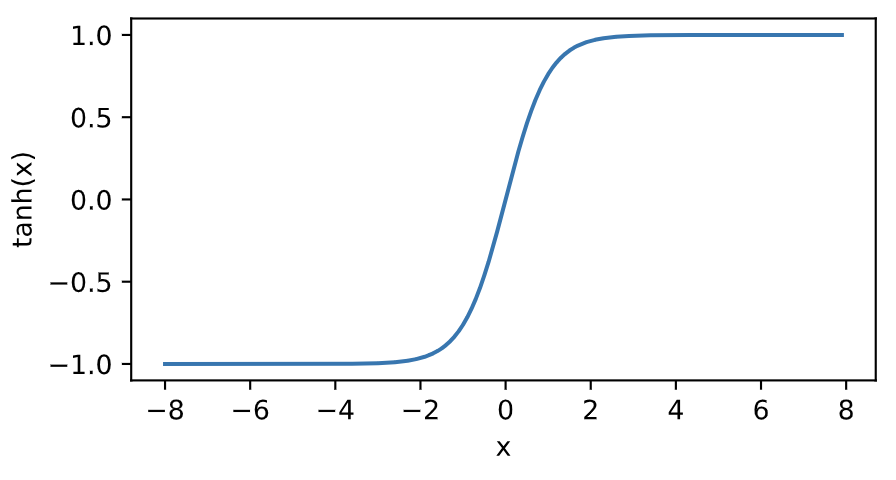
我们接着绘制tanh函数。当输入接近0时，tanh函数接近线性变换。虽然该函数的形状和sigmoid函数的形状很像，但tanh函数在坐标系的原点上对称。

y = x.tanh()
xyplot(x, y, 'tanh')

依据链式法则，tanh函数的导数

$${\text{tanh}}^{\prime }(x)=1?{\text{tanh}}^2(x).$$

下面绘制了tanh函数的导数。当输入为0时，tanh函数的导数达到最大值1；当输入越偏离0时，tanh函数的导数越接近0。

x.grad.zero_()
y.sum().backward()
xyplot(x, x.grad, 'grad of tanh')

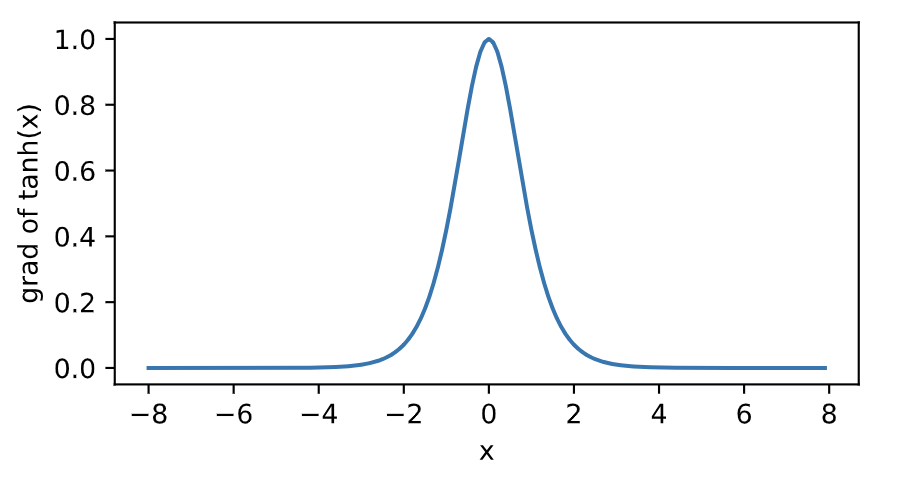
tanh（双曲正切）函数特点就是可以将元素的值变换到-1和1之间，他和sigmoid函数很相似，只是导数范围和输出范围不同，该函数计算量也大，会增加训练时间

3. 多层感知机

多层感知机就是含有至少一个隐藏层的由全连接层组成的神经网络，且每个隐藏层的输出通过激活函数进行变换。多层感知机的层数和各隐藏层中隐藏单元个数都是超参数。以单隐藏层为例并沿用本节之前定义的符号，多层感知机按以下方式计算输出：

$$\begin{array}{rl}\mathbf{H}& =?(\mathbf{X}{\mathbf{W}}_h+{\mathbf{b}}_h),\\ \mathbf{O}& =\mathbf{H}{\mathbf{W}}_o+{\mathbf{b}}_o,\end{array}$$

其中$?$表示激活函数。在分类问题中，我们可以对输出$\mathbf{O}$做softmax运算，并使用softmax回归中的交叉熵损失函数。
在回归问题中，我们将输出层的输出个数设为1，并将输出$\mathbf{O}$直接提供给线性回归中使用的平方损失函数。

由此可以得出多层感知机的模型计算方式就是将上一层的线性函数经过激活函数做非线性变换后输入到下一层，其中多层感知机的层数和各层隐藏单元数都是超参数（训练前需要指定超参数的值，和参数的区别在于，参数初始时一般都是随机值，随着训练进行优化）

4. 小结

• 多层感知机在输出层与输入层之间加入了一个或多个全连接隐藏层，并通过激活函数对隐藏层输出进行变换。
• 常用的激活函数包括ReLU函数、sigmoid函数和tanh函数。