1、 SIFT简介
- 尺度不变特征变换(Scale-invariantfeature transform),主要特点在于其多尺度信息描述,能够有效描述缩放,并且对 图像旋转、亮度、仿射变换、视角变化具有很好的适应性。
SIFT算法还具有如下一些特点:
1. 信息量丰富,即使少数的几个物体也可以产生大量的SIFT特征向量;
2. 特征区分度大,适用于在海量特征数据库中进行快速、准确的匹配;
3. 速度快,加速的SIFT算法可以达到实时。
- 算法首先要理解多尺度(多个分辨率)的概念,也就是我们常说的图像金字塔
,可以简单理解为图像的降采样,一般降采样过程分为两步:一是图像模糊,二是隔行采样。
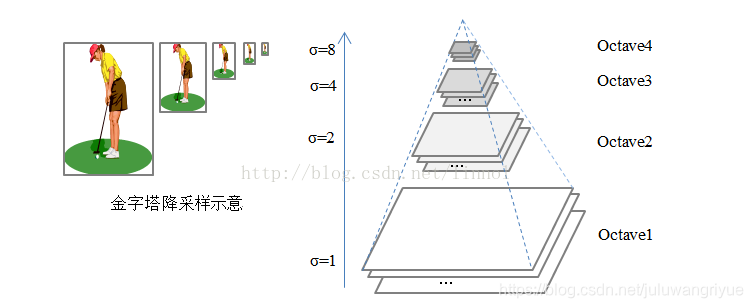
- 右侧是我们常说的高斯金字塔,所谓高斯金字塔在于上一级图像通过下一级图像进行高斯滤波得到,英文Octave是音乐上一个八度的意思,这里引申为一组分辨率相同的图像,一个Octave组采用了不同的高斯函数进行滤波,因此其模糊程度不一样,不同组的图像具有不同的分辨率(按照1/2降采样得到)。
- SIFT算法本质在于提取图像关键点,也就是在不同尺度空间下具有方向信息的局部极值点。(这些点不会因光照条件的改变而消失,比如角点、边缘点、暗区域的亮点以及亮区域的暗点)
- SIFT算法可以描述为以下步骤:
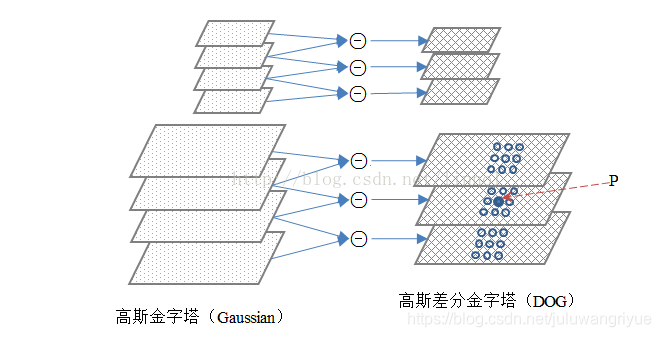
1.构建尺度空间
根据高斯滤波处理输入图像,得到高斯金字塔,并建立如上图所示的高斯差分金字塔(DOG);
2.极值点检测
候选点P与同一尺度,上下相邻两尺度空间内相邻的 26 个像素点进行比较,以确保在图像空间和尺度空间都检测到局部极值;
3.关键点筛选
选取在不同尺度(或者叫分辨率)下同时存在的极值点,称之为匹配点,匹配点不会因为尺度变化而消失。
参考:SIFT的来龙去脉-&- 个人代码实现(opencv3;C++)
参考:角点检测算子(Harris, KLT, SIFT,SUSAN)
2、代码实现
自己使用的opencv4.5.2
sift.h
#pragma once
/*************************************************************************************************************************
*文件说明:
* SIFT算法的实现头文件
*开发环境:
* Win10+VS2012+OpenCv2.4.8
*时间地点:
* 陕西师范大学.文津楼 2016.12.30
*再次修改时间:
* 陕西师范大学.文津楼 2017.2.24
*作者信息:
* 九月
**************************************************************************************************************************/
#ifndef SIFT_H
#define SIFT_H
#include <opencv2/opencv.hpp>
#include <opencv2/highgui.hpp>
#include <vector>
using namespace std;
using namespace cv;
typedef double pixel_t; //【1】像素类型
#define INIT_SIGMA 0.5 //【2】初始sigma
#define SIGMA 1.6
#define INTERVALS 3 //【3】高斯金字塔中每组图像中有三层/张图片
#define RATIO 10 //【4】半径r
#define MAX_INTERPOLATION_STEPS 5 //【5】最大空间间隔
#define DXTHRESHOLD 0.03 //【6】|D(x^)| < 0.03 0.03极值点太多
#define ORI_HIST_BINS 36 //【7】bings=36
#define ORI_SIGMA_TIMES 1.5
#define ORI_WINDOW_RADIUS 3.0 * ORI_SIGMA_TIMES
#define ORI_SMOOTH_TIMES 2
#define ORI_PEAK_RATIO 0.8
#define FEATURE_ELEMENT_LENGTH 128
#define DESCR_HIST_BINS 8
#define IMG_BORDER 5
#define DESCR_WINDOW_WIDTH 4
#define DESCR_SCALE_ADJUST 3
#define DESCR_MAG_THR 0.2
#define INT_DESCR_FCTR 512.0
/*********************************************************************************************
*模块说明:
* 关键点/特征点的结构体声明
*注意点1:
* 在高斯金字塔构建的过程中,一幅图像可以产生好几组(octave)图像,一组图像包含几层(inteval)
* 图像
*********************************************************************************************/
struct Keypoint
{
int octave; //【1】关键点所在组
int interval; //【2】关键点所在层
double offset_interval; //【3】调整后的层的增量
int x; //【4】x,y坐标,根据octave和interval可取的层内图像
int y;
double scale; //【5】空间尺度坐标scale = sigma0*pow(2.0, o+s/S)
double dx; //【6】特征点坐标,该坐标被缩放成原图像大小
double dy;
double offset_x;
double offset_y;
//============================================================
//1---高斯金字塔组内各层尺度坐标,不同组的相同层的sigma值相同
//2---关键点所在组的组内尺度
//============================================================
double octave_scale; //【1】offset_i;
double ori; //【2】方向
int descr_length;
double descriptor[FEATURE_ELEMENT_LENGTH]; //【3】特征点描述符
double val; //【4】极值
};
/*********************************************************************************
*模块说明:
* SIFT算法内,所有成员函数的声明
*********************************************************************************/
void read_features(vector<Keypoint>&features, const char*file);
void write_features(const vector<Keypoint>&features, const char*file);
void testInverse3D();
void write_pyr(const vector<Mat>& pyr, const char* dir);
void DrawKeyPoints(Mat &src, vector<Keypoint>& keypoints);
const char* GetFileName(const char* dir, int i);
void ConvertToGray(const Mat& src, Mat& dst);
void DownSample(const Mat& src, Mat& dst);
void UpSample(const Mat& src, Mat& dst);
void GaussianTemplateSmooth(const Mat &src, Mat &dst, double);
void GaussianSmooth2D(const Mat &src, Mat &dst, double sigma);
void GaussianSmooth(const Mat &src, Mat &dst, double sigma);
void Sift(const Mat &src, vector<Keypoint>& features, double sigma = SIGMA, int intervals = INTERVALS);
void CreateInitSmoothGray(const Mat &src, Mat &dst, double);
void GaussianPyramid(const Mat &src, vector<Mat>&gauss_pyr, int octaves, int intervals, double sigma);
void Sub(const Mat& a, const Mat& b, Mat & c);
void DogPyramid(const vector<Mat>& gauss_pyr, vector<Mat>& dog_pyr, int octaves, int intervals);
void DetectionLocalExtrema(const vector<Mat>& dog_pyr, vector<Keypoint>& extrema, int octaves, int intervals);
void DrawSiftFeatures(Mat& src, vector<Keypoint>& features);
#endif
sift.cpp
/*************************************************************************************************************************
*文件说明:
* SIFT算法的头文件所对应的实现文件
*开发环境:
* Win10+VS2012+OpenCv2.4.8
*时间地点:
* 陕西师范大学.文津楼 2016.12.30
*再次修改时间:
* 陕西师范大学.文津楼 2017.2.24
*作者信息:
* 九月
**************************************************************************************************************************/
#include"sift.h"
#include<fstream>
#include<iostream>
using namespace std;
using namespace cv;
/*************************************************************************************************************************
*模块说明:
* 图像灰度化函数----将彩色图像转为灰度图像
**************************************************************************************************************************/
void ConvertToGray(const Mat& src, Mat& dst)
{
cv::Size size = src.size();
if (dst.empty())
dst.create(size, CV_64F); //[1]利用Mat类的成员函数创建Mat容器
uchar* srcData = src.data; //[2]指向存储所有像素值的矩阵的数据区域
pixel_t* dstData = (pixel_t*)dst.data; //[3]指向dst的矩阵体数据区域
int dstStep = dst.step / sizeof(dstData[0]); //[4]一行图像含有多少字节数
for (int j = 0; j<src.cols; j++)
{
for (int i = 0; i<src.rows; i++)
{
double b = (srcData + src.step*i + src.channels()*j)[0] / 255.0;
double g = (srcData + src.step*i + src.channels()*j)[1] / 255.0;
double r = (srcData + src.step*i + src.channels()*j)[2] / 255.0;
*(dstData + dstStep*i + dst.channels()*j) = (r + g + b) / 3.0;
}
}
}
/*************************************************************************************************************************
*模块说明:
* 隔点采样
**************************************************************************************************************************/
void DownSample(const Mat& src, Mat& dst)
{
if (src.channels() != 1)
return;
if (src.cols <= 1 || src.rows <= 1)
{
src.copyTo(dst);
return;
}
dst.create((int)(src.rows / 2), (int)(src.cols / 2), src.type());
pixel_t* srcData = (pixel_t*)src.data;
pixel_t* dstData = (pixel_t*)dst.data;
int srcStep = src.step / sizeof(srcData[0]);
int dstStep = dst.step / sizeof(dstData[0]);
int m = 0, n = 0;
for (int j = 0; j < src.cols; j += 2, n++)
{
m = 0;
for (int i = 0; i < src.rows; i += 2, m++)
{
pixel_t sample = *(srcData + srcStep * i + src.channels() * j);
if (m < dst.rows && n < dst.cols)
{
*(dstData + dstStep * m + dst.channels() * n) = sample;
}
}
}
}
/*************************************************************************************************************************
*模块说明:
* 线性插值放大
**************************************************************************************************************************/
void UpSample(const Mat &src, Mat &dst)
{
if (src.channels() != 1)
return;
dst.create(src.rows * 2, src.cols * 2, src.type());
pixel_t* srcData = (pixel_t*)src.data;
pixel_t* dstData = (pixel_t*)dst.data;
int srcStep = src.step / sizeof(srcData[0]);
int dstStep = dst.step / sizeof(dstData[0]);
int m = 0, n = 0;
for (int j = 0; j < src.cols - 1; j++, n += 2)
{
m = 0;
for (int i = 0; i < src.rows - 1; i++, m += 2)
{
double sample = *(srcData + srcStep * i + src.channels() * j);
*(dstData + dstStep * m + dst.channels() * n) = sample;
double rs = *(srcData + srcStep * (i)+src.channels()*j) + (*(srcData + srcStep * (i + 1) + src.channels()*j));
*(dstData + dstStep * (m + 1) + dst.channels() * n) = rs / 2;
double cs = *(srcData + srcStep * i + src.channels()*(j)) + (*(srcData + srcStep * i + src.channels()*(j + 1)));
*(dstData + dstStep * m + dst.channels() * (n + 1)) = cs / 2;
double center = (*(srcData + srcStep * (i + 1) + src.channels() * j))
+ (*(srcData + srcStep * i + src.channels() * j))
+ (*(srcData + srcStep * (i + 1) + src.channels() * (j + 1)))
+ (*(srcData + srcStep * i + src.channels() * (j + 1)));
*(dstData + dstStep * (m + 1) + dst.channels() * (n + 1)) = center / 4;
}
}
if (dst.rows < 3 || dst.cols < 3)
return;
//最后两行两列
for (int k = dst.rows - 1; k >= 0; k--)
{
*(dstData + dstStep *(k)+dst.channels()*(dst.cols - 2)) = *(dstData + dstStep *(k)+dst.channels()*(dst.cols - 3));
*(dstData + dstStep *(k)+dst.channels()*(dst.cols - 1)) = *(dstData + dstStep *(k)+dst.channels()*(dst.cols - 3));
}
for (int k = dst.cols - 1; k >= 0; k--)
{
*(dstData + dstStep *(dst.rows - 2) + dst.channels()*(k)) = *(dstData + dstStep *(dst.rows - 3) + dst.channels()*(k));
*(dstData + dstStep *(dst.rows - 1) + dst.channels()*(k)) = *(dstData + dstStep *(dst.rows - 3) + dst.channels()*(k));
}
}
/*************************************************************************************************************************
*模块说明:
* OpenCv中的高斯平滑函数
**************************************************************************************************************************/
void GaussianSmooth(const Mat &src, Mat &dst, double sigma)
{
GaussianBlur(src, dst, Size(0, 0), sigma, sigma);
}
/*************************************************************************************************************************
*模块说明:
* 模块1--创建初始灰度图像------初始图像先将原图像灰度化,再扩大一倍后,使用高斯模糊平滑
*功能说明:
* 在最开始建立高斯金字塔的时候,要预先模糊输入的图像来作为第0个组的第0层图像,这时相当于丢弃了最高的空域的采样率。因
* 此,通常的做法是先将图像的尺度扩大一倍来生成第-1组。我们假定初始的输入图像为了抗击混淆现象,已经对其进行了sigma=0.5
* 的高斯模糊,如果输入图像的尺寸用双线性插值扩大一倍,那么相当于sigma=1.0
*这样做的原因:
* 在检测极值点前,对原始图像的高斯平滑以致图像丢失高频信息,所以Lowe建议在建立尺度空间前,首先对原始图像长宽扩展一倍,
* 以便保留原始图像的信息(特别是图像的高频信息,比如边缘,角点),增加特征点的数量。
*函数功能:
* 这个函数的作用是用于创建高斯金字塔的-1层图像
*代码解读:
* 2017.2.24----陕西师范大学
**************************************************************************************************************************/
void CreateInitSmoothGray(const Mat &src, Mat &dst, double sigma = SIGMA)
{
cv::Mat gray; //[1]保存原始图像的灰度图像
cv::Mat up; //[2]保存原始图像的上采样图像
ConvertToGray(src, gray);
UpSample(gray, up); //[3]图像的上采样
//[4]高斯金字塔的-1组的sigma的计算公式
double sigma_init = sqrt(sigma * sigma - (INIT_SIGMA * 2) * (INIT_SIGMA * 2));//[1]-1层的sigma
GaussianSmooth(up, dst, sigma_init); //[5]高斯平滑
}
/*************************************************************************************************************************
*模块说明:
* 模块二:3.3 图像高斯金字塔的构建
**************************************************************************************************************************/
void GaussianPyramid(const Mat &src, vector<Mat>&gauss_pyr, int octaves, int intervals = INTERVALS, double sigma = SIGMA)
{
double *sigmas = new double[intervals + 3];
double k = pow(2.0, 1.0 / intervals);
sigmas[0] = sigma;
double sig_prev;
double sig_total;
for (int i = 1; i < intervals + 3; i++)
{
sig_prev = pow(k, i - 1) * sigma;
sig_total = sig_prev * k;
sigmas[i] = sqrt(sig_total * sig_total - sig_prev * sig_prev);
}
for (int o = 0; o < octaves; o++)
{
//每组多三层
for (int i = 0; i < intervals + 3; i++)
{
Mat mat;
if (o == 0 && i == 0)
{
src.copyTo(mat);
}
else if (i == 0)
{
DownSample(gauss_pyr[(o - 1)*(intervals + 3) + intervals], mat);
}
else
{
GaussianSmooth(gauss_pyr[o * (intervals + 3) + i - 1], mat, sigmas[i]);
}
gauss_pyr.push_back(mat);
}
}
delete[] sigmas;
}
/*************************************************************************************************************************
*模块说明:
* 图像的差分
**************************************************************************************************************************/
void Sub(const Mat& a, const Mat& b, Mat & c)
{
if (a.rows != b.rows || a.cols != b.cols || a.type() != b.type())
return;
if (!c.empty())
return;
c.create(a.size(), a.type());
pixel_t* ap = (pixel_t*)a.data;
pixel_t* ap_end = (pixel_t*)a.dataend;
pixel_t* bp = (pixel_t*)b.data;
pixel_t* cp = (pixel_t*)c.data;
int step = a.step / sizeof(pixel_t);
while (ap != ap_end)
{
*cp++ = *ap++ - *bp++;
}
}
/*************************************************************************************************************************
*模块说明:
* 模块三:3.4 高斯差分金字塔
*功能说明:
* 1--2002年,Mikolajczyk在详细的实验比较中发现尺度归一化的高斯拉普拉斯函数的极大值和极小值同其他的特征提取函数,例如:
* 梯度,Hessian或者Harris角点特征比较,能够产生稳定的图像特征。
* 2--而Lindberg早在1994年发现高斯差分函数(Difference of Gaussian,简称DOG算子)与尺度归一化的拉普拉斯函数非常相似,因此,
* 利用图像间的差分代替微分。
**************************************************************************************************************************/
void DogPyramid(const vector<Mat>& gauss_pyr, vector<Mat>& dog_pyr, int octaves, int intervals = INTERVALS)
{
for (int o = 0; o < octaves; o++)
{
for (int i = 1; i < intervals + 3; i++)
{
Mat mat;
Sub(gauss_pyr[o*(intervals + 3) + i], gauss_pyr[o*(intervals + 3) + i - 1], mat);
dog_pyr.push_back(mat);
}
}
}
/*************************************************************************************************************************
*模块说明:
* 模块四的第一步:3.4-空间极值点的初步检测(关键点的初步探查)
*功能说明:
* 1--在高斯差分函数之后,得到一系列的关键点的疑似点,我们需要对这些关键点的疑似点初步进行检测和筛选
* 2--此块代码所根据的原理为CSDN博客中的:3.5空间极值点的检测
**************************************************************************************************************************/
bool isExtremum(int x, int y, const vector<Mat>& dog_pyr, int index)
{
pixel_t * data = (pixel_t *)dog_pyr[index].data;
int step = dog_pyr[index].step / sizeof(data[0]);
pixel_t val = *(data + y*step + x);
if (val > 0)
{
for (int i = -1; i <= 1; i++)
{
int stp = dog_pyr[index + i].step / sizeof(data[0]);
for (int j = -1; j <= 1; j++)
{
for (int k = -1; k <= 1; k++)
{
if (val < *((pixel_t*)dog_pyr[index + i].data + stp*(y + j) + (x + k)))
{
return false;
}
}
}
}
}
else
{
for (int i = -1; i <= 1; i++)
{
int stp = dog_pyr[index + i].step / sizeof(pixel_t);
for (int j = -1; j <= 1; j++)
{
for (int k = -1; k <= 1; k++)
{
//检查最小极值
if (val > *((pixel_t*)dog_pyr[index + i].data + stp*(y + j) + (x + k)))
{
return false;
}
}
}
}
}
return true;
}
/*************************************************************************************************************************
*模块说明:
* 模块四的第三步:4.2--消除边缘响应点
*功能说明:
* 1)一个定义不好的高斯差分算子的极值在横跨边缘的地方有较大的住主曲率,在垂直边缘的方向有较小的主曲率。
* 2)DOG算子会产生较强的边缘响应,需要剔除不稳定的边缘响应点,获取特征点处的Hessian矩阵,主曲率通过一个2*2的Hessian矩
* 阵H求出
* 3)主曲率D和Hessian矩阵的特征值成正比,公式(r+1)*(r+1)/r的值在两个特征值相等时最小;这个值越大,说明两个特征值的比值
* 越大,即在某一个方向的梯度值越大,而在另一个方向的梯度值越小,而边缘恰恰就是这种情况。所以,为了剔除边缘响应点,
* 需要让该比值小于一定的阈值,因此,为了检测主曲率是否在某阈值r下,只需检测。CSDN论文中的公式(4-7成立),成立,将关
* 键点保留,反之,剔除。
**************************************************************************************************************************/
#define DAt(x, y) (*(data+(y)*step+(x)))
bool passEdgeResponse(int x, int y, const vector<Mat>& dog_pyr, int index, double r = RATIO)
{
pixel_t *data = (pixel_t *)dog_pyr[index].data;
int step = dog_pyr[index].step / sizeof(data[0]);
pixel_t val = *(data + y*step + x);
double Dxx;
double Dyy;
double Dxy;
double Tr_h; //[1]Hessian矩阵的迹
double Det_h; //[2]Hessian矩阵所对应的行列式的值
Dxx = DAt(x + 1, y) + DAt(x - 1, y) - 2 * val;
Dyy = DAt(x, y + 1) + DAt(x, y - 1) - 2 * val;
Dxy = (DAt(x + 1, y + 1) + DAt(x - 1, y - 1) - DAt(x - 1, y + 1) - DAt(x + 1, y - 1)) / 4.0;
Tr_h = Dxx + Dyy;
Det_h = Dxx * Dyy - Dxy * Dxy;
if (Det_h <= 0)return false;
if (Tr_h * Tr_h / Det_h < (r + 1) * (r + 1) / r) return true;
return false;
}
/*************************************************************************************************************************
*模块说明:
* 有限差分求导?
**************************************************************************************************************************/
#define Hat(i, j) (*(H+(i)*3 + (j)))
double PyrAt(const vector<Mat>& pyr, int index, int x, int y)
{
pixel_t *data = (pixel_t*)pyr[index].data;
int step = pyr[index].step / sizeof(data[0]);
pixel_t val = *(data + y*step + x);
return val;
}
/*************************************************************************************************************************
*模块说明:
* 有限差分求导?
**************************************************************************************************************************/
#define At(index, x, y) (PyrAt(dog_pyr, (index), (x), (y)))
//3维D(x)一阶偏导,dx列向量
void DerivativeOf3D(int x, int y, const vector<Mat>& dog_pyr, int index, double *dx)
{
double Dx = (At(index, x + 1, y) - At(index, x - 1, y)) / 2.0;
double Dy = (At(index, x, y + 1) - At(index, x, y - 1)) / 2.0;
double Ds = (At(index + 1, x, y) - At(index - 1, x, y)) / 2.0;
dx[0] = Dx;
dx[1] = Dy;
dx[2] = Ds;
}
//3维D(x)二阶偏导,即Hessian矩阵
void Hessian3D(int x, int y, const vector<Mat>& dog_pyr, int index, double *H)
{
double val, Dxx, Dyy, Dss, Dxy, Dxs, Dys;
val = At(index, x, y);
Dxx = At(index, x + 1, y) + At(index, x - 1, y) - 2 * val;
Dyy = At(index, x, y + 1) + At(index, x, y - 1) - 2 * val;
Dss = At(index + 1, x, y) + At(index - 1, x, y) - 2 * val;
Dxy = (At(index, x + 1, y + 1) + At(index, x - 1, y - 1)
- At(index, x + 1, y - 1) - At(index, x - 1, y + 1)) / 4.0;
Dxs = (At(index + 1, x + 1, y) + At(index - 1, x - 1, y)
- At(index - 1, x + 1, y) - At(index + 1, x - 1, y)) / 4.0;
Dys = (At(index + 1, x, y + 1) + At(index - 1, x, y - 1)
- At(index + 1, x, y - 1) - At(index - 1, x, y + 1)) / 4.0;
Hat(0, 0) = Dxx;
Hat(1, 1) = Dyy;
Hat(2, 2) = Dss;
Hat(1, 0) = Hat(0, 1) = Dxy;
Hat(2, 0) = Hat(0, 2) = Dxs;
Hat(2, 1) = Hat(1, 2) = Dys;
}
/*************************************************************************************************************************
*模块说明:
* 4.4 三阶矩阵求逆
**************************************************************************************************************************/
#define HIat(i, j) (*(H_inve+(i)*3 + (j)))
//3*3阶矩阵求逆
bool Inverse3D(const double *H, double *H_inve)
{
double A = Hat(0, 0)*Hat(1, 1)*Hat(2, 2)
+ Hat(0, 1)*Hat(1, 2)*Hat(2, 0)
+ Hat(0, 2)*Hat(1, 0)*Hat(2, 1)
- Hat(0, 0)*Hat(1, 2)*Hat(2, 1)
- Hat(0, 1)*Hat(1, 0)*Hat(2, 2)
- Hat(0, 2)*Hat(1, 1)*Hat(2, 0);
if (fabs(A) < 1e-10) return false;
HIat(0, 0) = Hat(1, 1) * Hat(2, 2) - Hat(2, 1)*Hat(1, 2);
HIat(0, 1) = -(Hat(0, 1) * Hat(2, 2) - Hat(2, 1) * Hat(0, 2));
HIat(0, 2) = Hat(0, 1) * Hat(1, 2) - Hat(0, 2)*Hat(1, 1);
HIat(1, 0) = Hat(1, 2) * Hat(2, 0) - Hat(2, 2)*Hat(1, 0);
HIat(1, 1) = -(Hat(0, 2) * Hat(2, 0) - Hat(0, 0) * Hat(2, 2));
HIat(1, 2) = Hat(0, 2) * Hat(1, 0) - Hat(0, 0)*Hat(1, 2);
HIat(2, 0) = Hat(1, 0) * Hat(2, 1) - Hat(1, 1)*Hat(2, 0);
HIat(2, 1) = -(Hat(0, 0) * Hat(2, 1) - Hat(0, 1) * Hat(2, 0));
HIat(2, 2) = Hat(0, 0) * Hat(1, 1) - Hat(0, 1)*Hat(1, 0);
for (int i = 0; i < 9; i++)
{
*(H_inve + i) /= A;
}
return true;
}
/*************************************************************************************************************************
*模块说明:
*
**************************************************************************************************************************/
//计算x^
void GetOffsetX(int x, int y, const vector<Mat>& dog_pyr, int index, double *offset_x)
{
//x^ = -H^(-1) * dx; dx = (Dx, Dy, Ds)^T
double H[9], H_inve[9] = { 0 };
Hessian3D(x, y, dog_pyr, index, H);
Inverse3D(H, H_inve);
double dx[3];
DerivativeOf3D(x, y, dog_pyr, index, dx);
for (int i = 0; i < 3; i++)
{
offset_x[i] = 0.0;
for (int j = 0; j < 3; j++)
{
offset_x[i] += H_inve[i * 3 + j] * dx[j];
}
offset_x[i] = -offset_x[i];
}
}
//计算|D(x^)|
double GetFabsDx(int x, int y, const vector<Mat>& dog_pyr, int index, const double* offset_x)
{
//|D(x^)|=D + 0.5 * dx * offset_x; dx=(Dx, Dy, Ds)^T
double dx[3];
DerivativeOf3D(x, y, dog_pyr, index, dx);
double term = 0.0;
for (int i = 0; i < 3; i++)
term += dx[i] * offset_x[i];
pixel_t *data = (pixel_t *)dog_pyr[index].data;
int step = dog_pyr[index].step / sizeof(data[0]);
pixel_t val = *(data + y*step + x);
return fabs(val + 0.5 * term);
}
/*************************************************************************************************************************
*模块说明:
* 模块四的第二步:修正极值点,删除不稳定的点
*功能说明:
* 1--根据高斯差分函数产生的极值点并不全都是稳定的特征点,因为某些极值点的响应较弱,而且DOG算子会产生较强的边缘响应
* 2--以上方法检测到的极值点是离散空间的极值点,下面通过拟合三维二次函数来精确定位关键点的位置和尺度,同时去除对比度
* 低和不稳定的边缘响应点(因为DOG算子会产生较强的边缘响应),以增强匹配的稳定性、提高抗噪声的能力。
* 3--修正极值点,删除不稳定点,|D(x)| < 0.03 Lowe 2004
**************************************************************************************************************************/
Keypoint* InterploationExtremum(int x, int y, const vector<Mat>& dog_pyr, int index, int octave, int interval, double dxthreshold = DXTHRESHOLD)
{
//计算x=(x,y,sigma)^T
//x^ = -H^(-1) * dx; dx = (Dx, Dy, Ds)^T
double offset_x[3] = { 0 };
const Mat &mat = dog_pyr[index];
int idx = index;
int intvl = interval;
int i = 0;
while (i < MAX_INTERPOLATION_STEPS)
{
GetOffsetX(x, y, dog_pyr, idx, offset_x);
//4. Accurate keypoint localization. Lowe
//如果offset_x 的任一维度大于0.5,it means that the extremum lies closer to a different sample point.
if (fabs(offset_x[0]) < 0.5 && fabs(offset_x[1]) < 0.5 && fabs(offset_x[2]) < 0.5)
break;
//用周围的点代替
x += cvRound(offset_x[0]);
y += cvRound(offset_x[1]);
interval += cvRound(offset_x[2]);
idx = index - intvl + interval;
//此处保证检测边时 x+1,y+1和x-1, y-1有效
if (interval < 1 || interval > INTERVALS || x >= mat.cols - 1 || x < 2 || y >= mat.rows - 1 || y < 2)
{
return NULL;
}
i++;
}
//窜改失败
if (i >= MAX_INTERPOLATION_STEPS)
return NULL;
//rejecting unstable extrema
//|D(x^)| < 0.03取经验值
if (GetFabsDx(x, y, dog_pyr, idx, offset_x) < dxthreshold / INTERVALS)
{
return NULL;
}
Keypoint *keypoint = new Keypoint;
keypoint->x = x;
keypoint->y = y;
keypoint->offset_x = offset_x[0];
keypoint->offset_y = offset_x[1];
keypoint->interval = interval;
keypoint->offset_interval = offset_x[2];
keypoint->octave = octave;
keypoint->dx = (x + offset_x[0])*pow(2.0, octave);
keypoint->dy = (y + offset_x[1])*pow(2.0, octave);
return keypoint;
}
/*************************************************************************************************************************
*模块说明:
* 模块四:3.5 空间极值点的检测(关键点的初步探查)
*功能说明:
* 1--关键点是由DOG空间的局部极值点组成的,关键点的初步探查是通过同一组内各DoG相邻两层图像之间的比较完成的。为了寻找DoG
* 函数的极值点,每一个像素点都要和它所有相邻的点比较,看其是否比它的图像域和尺度域相邻的点大还是小。
* 2--当然这样产生的极值点并不全都是稳定的特征点,因为某些极值点相应较弱,而且DOG算子会产生较强的边缘响应。
**************************************************************************************************************************/
void DetectionLocalExtrema(const vector<Mat>& dog_pyr, vector<Keypoint>& extrema, int octaves, int intervals = INTERVALS)
{
double thresh = 0.5 * DXTHRESHOLD / intervals;
for (int o = 0; o < octaves; o++)
{
//第一层和最后一层极值忽略
for (int i = 1; i < (intervals + 2) - 1; i++)
{
int index = o*(intervals + 2) + i; //[1]图片索引的定位
pixel_t *data = (pixel_t *)dog_pyr[index].data; //[2]获取图片的矩阵体的首地址
int step = dog_pyr[index].step / sizeof(data[0]); //[3]说明矩阵在存储空间中的存储是以线性空间的方式存放的
for (int y = IMG_BORDER; y < dog_pyr[index].rows - IMG_BORDER; y++)
{
for (int x = IMG_BORDER; x < dog_pyr[index].cols - IMG_BORDER; x++)
{
pixel_t val = *(data + y*step + x);
if (std::fabs(val) > thresh) //[4]排除阈值过小的点
{
if (isExtremum(x, y, dog_pyr, index)) //[5]判断是否是极值
{
Keypoint *extrmum = InterploationExtremum(x, y, dog_pyr, index, o, i);
if (extrmum)
{
if (passEdgeResponse(extrmum->x, extrmum->y, dog_pyr, index))
{
extrmum->val = *(data + extrmum->y*step + extrmum->x);
extrema.push_back(*extrmum);
}
delete extrmum;
}//extrmum
}//isExtremum
}//std::fabs
}//for x
}//for y
}
}
}
/*************************************************************************************************************************
*模块说明:
* 模块五:
*功能说明:
*
**************************************************************************************************************************/
void CalculateScale(vector<Keypoint>& features, double sigma = SIGMA, int intervals = INTERVALS)
{
double intvl = 0;
for (int i = 0; i < features.size(); i++)
{
intvl = features[i].interval + features[i].offset_interval;
features[i].scale = sigma * pow(2.0, features[i].octave + intvl / intervals);
features[i].octave_scale = sigma * pow(2.0, intvl / intervals);
}
}
//对扩大的图像特征缩放
void HalfFeatures(vector<Keypoint>& features)
{
for (int i = 0; i < features.size(); i++)
{
features[i].dx /= 2;
features[i].dy /= 2;
features[i].scale /= 2;
}
}
/********************************************************************************************************************************
*模块说明:
* 模块六---步骤2:计算关键点的梯度和梯度方向
*功能说明:
* 1)计算关键点(x,y)处的梯度幅值和梯度方向
* 2)将所计算出来的梯度幅值和梯度方向保存在变量mag和ori中
*********************************************************************************************************************************/
bool CalcGradMagOri(const Mat& gauss, int x, int y, double& mag, double& ori)
{
if (x > 0 && x < gauss.cols - 1 && y > 0 && y < gauss.rows - 1)
{
pixel_t *data = (pixel_t*)gauss.data;
int step = gauss.step / sizeof(*data);
double dx = *(data + step*y + (x + 1)) - (*(data + step*y + (x - 1))); //[1]利用X方向上的差分代替微分dx
double dy = *(data + step*(y + 1) + x) - (*(data + step*(y - 1) + x)); //[2]利用Y方向上的差分代替微分dy
mag = sqrt(dx*dx + dy*dy); //[3]计算该关键点的梯度幅值
ori = atan2(dy, dx); //[4]计算该关键点的梯度方向
return true;
}
else
return false;
}
/********************************************************************************************************************************
*模块说明:
* 模块六---步骤1:计算梯度的方向直方图
*功能说明:
* 1)直方图以每10度为一个柱,共36个柱,柱代表的方向为为像素点的梯度方向,柱的长短代表了梯度幅值。
* 2)根据Lowe的建议,直方图统计采用3*1.5*sigma
* 3)在直方图统计时,每相邻三个像素点采用高斯加权,根据Lowe的建议,模板采用[0.25,0.5,0.25],并且连续加权两次
*结 论:
* 图像的关键点检测完毕后,每个关键点就拥有三个信息:位置、尺度、方向;同时也就使关键点具备平移、缩放和旋转不变性
*********************************************************************************************************************************/
double* CalculateOrientationHistogram(const Mat& gauss, int x, int y, int bins, int radius, double sigma)
{
double* hist = new double[bins]; //[1]动态分配一个double类型的数组
for (int i = 0; i < bins; i++) //[2]给这个数组初始化
*(hist + i) = 0.0;
double mag; //[3]关键点的梯度幅值
double ori; //[4]关键点的梯度方向
double weight;
int bin;
const double PI2 = 2.0*CV_PI;
double econs = -1.0 / (2.0*sigma*sigma);
for (int i = -radius; i <= radius; i++)
{
for (int j = -radius; j <= radius; j++)
{
if (CalcGradMagOri(gauss, x + i, y + j, mag, ori)) //[5]计算该关键点的梯度幅值和方向
{
weight = exp((i*i + j*j)*econs);
bin = cvRound(bins * (CV_PI - ori) / PI2); //[6]对一个double行的数进行四舍五入,返回一个整形的数
bin = bin < bins ? bin : 0;
hist[bin] += mag * weight; //[7]统计梯度的方向直方图
}
}
}
return hist;
}
/********************************************************************************************************************************
*模块说明:
* 模块六---步骤3:对梯度方向直方图进行连续两次的高斯平滑
*功能说明:
* 1)在直方图统计时,每相邻三个像素点采用高斯加权,根据Lowe的建议,模板采用[0.25,0.5,0.25],并且连续加权两次
* 2)对直方图进行两次平滑
*********************************************************************************************************************************/
void GaussSmoothOriHist(double *hist, int n)
{
double prev = hist[n - 1];
double temp;
double h0 = hist[0];
for (int i = 0; i < n; i++)
{
temp = hist[i];
hist[i] = 0.25 * prev + 0.5 * hist[i] + 0.25 * (i + 1 >= n ? h0 : hist[i + 1]);//对方向直方图进行高斯平滑
prev = temp;
}
}
/********************************************************************************************************************************
*模块说明:
* 模块六---步骤4:计算方向直方图中的主方向
*********************************************************************************************************************************/
double DominantDirection(double *hist, int n)
{
double maxd = hist[0];
for (int i = 1; i < n; i++)
{
if (hist[i] > maxd) //求取36个柱中的最大峰值
maxd = hist[i];
}
return maxd;
}
void CopyKeypoint(const Keypoint& src, Keypoint& dst)
{
dst.dx = src.dx;
dst.dy = src.dy;
dst.interval = src.interval;
dst.octave = src.octave;
dst.octave_scale = src.octave_scale;
dst.offset_interval = src.offset_interval;
dst.offset_x = src.offset_x;
dst.offset_y = src.offset_y;
dst.ori = src.ori;
dst.scale = src.scale;
dst.val = src.val;
dst.x = src.x;
dst.y = src.y;
}
/********************************************************************************************************************************
*模块说明:
* 模块六---步骤5:计算更加精确的关键点主方向----抛物插值
*功能说明:
* 1)方向直方图的峰值则代表了该特征点的方向,以直方图中的最大值作为该关键点的主方向。为了增强匹配的鲁棒性,只保留峰值大于主
* 方向峰值80%的方向作为改关键点的辅方向。因此,对于同一梯度值得多个峰值的关键点位置,在相同位置和尺度将会有多个关键点被
* 创建但方向不同。仅有15%的关键点被赋予多个方向,但是可以明显的提高关键点的稳定性。
* 2)在实际编程中,就是把该关键点复制成多份关键点,并将方向值分别赋给这些复制后的关键点
* 3)并且,离散的梯度直方图要进行【插值拟合处理】,来求得更加精确的方向角度值
*********************************************************************************************************************************/
#define Parabola_Interpolate(l, c, r) (0.5*((l)-(r))/((l)-2.0*(c)+(r)))
void CalcOriFeatures(const Keypoint& keypoint, vector<Keypoint>& features, const double *hist, int n, double mag_thr)
{
double bin;
double PI2 = CV_PI * 2.0;
int l;
int r;
for (int i = 0; i < n; i++)
{
l = (i == 0) ? n - 1 : i - 1;
r = (i + 1) % n;
//hist[i]是极值
if (hist[i] > hist[l] && hist[i] > hist[r] && hist[i] >= mag_thr)
{
bin = i + Parabola_Interpolate(hist[l], hist[i], hist[r]);
bin = (bin < 0) ? (bin + n) : (bin >= n ? (bin - n) : bin);
Keypoint new_key;
CopyKeypoint(keypoint, new_key);
new_key.ori = ((PI2 * bin) / n) - CV_PI;
features.push_back(new_key);
}
}
}
/********************************************************************************************************************************
*模块说明:
* 模块六:5 关键点方向分配
*功能说明:
* 1)为了使描述符具有旋转不变性,需要利用图像的局部特征为每一个关键点分配一个基准方向。使用图像梯度的方法求取局部结构的稳定
* 方向。
* 2)对于在DOG金字塔中检测出来的关键点,采集其所在高斯金字塔图像3sigma邻域窗口内像素的梯度和方向梯度和方向特征。
* 3)梯度的模和方向如下所示:
* 4) 在完成关键点的梯度计算后,使用直方图统计邻域内像素的梯度和方向。梯度直方图将0~360度的方向范围分为36个柱,其中每柱10度,
* 如图5.1所示,直方图的峰值方向代表了关键点的主方向
*********************************************************************************************************************************/
void OrientationAssignment(vector<Keypoint>& extrema, vector<Keypoint>& features, const vector<Mat>& gauss_pyr)
{
int n = extrema.size();
double *hist;
for (int i = 0; i < n; i++)
{
hist = CalculateOrientationHistogram(gauss_pyr[extrema[i].octave*(INTERVALS + 3) + extrema[i].interval],
extrema[i].x, extrema[i].y, ORI_HIST_BINS, cvRound(ORI_WINDOW_RADIUS*extrema[i].octave_scale),
ORI_SIGMA_TIMES*extrema[i].octave_scale); //[1]计算梯度的方向直方图
for (int j = 0; j < ORI_SMOOTH_TIMES; j++)
GaussSmoothOriHist(hist, ORI_HIST_BINS); //[2]对方向直方图进行高斯平滑
double highest_peak = DominantDirection(hist, ORI_HIST_BINS); //[3]求取方向直方图中的峰值
//[4]计算更加精确的关键点主方向
CalcOriFeatures(extrema[i], features, hist, ORI_HIST_BINS, highest_peak*ORI_PEAK_RATIO);
delete[] hist;
}
}
void InterpHistEntry(double ***hist, double xbin, double ybin, double obin, double mag, int bins, int d)
{
double d_r, d_c, d_o, v_r, v_c, v_o;
double** row, *h;
int r0, c0, o0, rb, cb, ob, r, c, o;
r0 = cvFloor(ybin);
c0 = cvFloor(xbin);
o0 = cvFloor(obin);
d_r = ybin - r0;
d_c = xbin - c0;
d_o = obin - o0;
/*
做插值:
xbin,ybin,obin:种子点所在子窗口的位置和方向
所有种子点都将落在4*4的窗口中
r0,c0取不大于xbin,ybin的正整数
r0,c0只能取到0,1,2
xbin,ybin在(-1, 2)
r0取不大于xbin的正整数时。
r0+0 <= xbin <= r0+1
mag在区间[r0,r1]上做插值
obin同理
*/
for (r = 0; r <= 1; r++)
{
rb = r0 + r;
if (rb >= 0 && rb < d)
{
v_r = mag * ((r == 0) ? 1.0 - d_r : d_r);
row = hist[rb];
for (c = 0; c <= 1; c++)
{
cb = c0 + c;
if (cb >= 0 && cb < d)
{
v_c = v_r * ((c == 0) ? 1.0 - d_c : d_c);
h = row[cb];
for (o = 0; o <= 1; o++)
{
ob = (o0 + o) % bins;
v_o = v_c * ((o == 0) ? 1.0 - d_o : d_o);
h[ob] += v_o;
}
}
}
}
}
}
/********************************************************************************************************************************
*模块说明:
* 模块七--步骤1:计算描述子的直方图
*功能说明:
*
*********************************************************************************************************************************/
double*** CalculateDescrHist(const Mat& gauss, int x, int y, double octave_scale, double ori, int bins, int width)
{
double ***hist = new double**[width];
for (int i = 0; i < width; i++)
{
hist[i] = new double*[width];
for (int j = 0; j < width; j++)
{
hist[i][j] = new double[bins];
}
}
for (int r = 0; r < width; r++)
for (int c = 0; c < width; c++)
for (int o = 0; o < bins; o++)
hist[r][c][o] = 0.0;
double cos_ori = cos(ori);
double sin_ori = sin(ori);
//6.1高斯权值,sigma等于描述字窗口宽度的一半
double sigma = 0.5 * width;
double conste = -1.0 / (2 * sigma*sigma);
double PI2 = CV_PI * 2;
double sub_hist_width = DESCR_SCALE_ADJUST * octave_scale;
//【1】计算描述子所需的图像领域区域的半径
int radius = (sub_hist_width*sqrt(2.0)*(width + 1)) / 2.0 + 0.5; //[1]0.5取四舍五入
double grad_ori;
double grad_mag;
for (int i = -radius; i <= radius; i++)
{
for (int j = -radius; j <= radius; j++)
{
double rot_x = (cos_ori * j - sin_ori * i) / sub_hist_width;
double rot_y = (sin_ori * j + cos_ori * i) / sub_hist_width;
double xbin = rot_x + width / 2 - 0.5; //[2]xbin,ybin为落在4*4窗口中的下标值
double ybin = rot_y + width / 2 - 0.5;
if (xbin > -1.0 && xbin < width && ybin > -1.0 && ybin < width)
{
if (CalcGradMagOri(gauss, x + j, y + i, grad_mag, grad_ori)) //[3]计算关键点的梯度方向
{
grad_ori = (CV_PI - grad_ori) - ori;
while (grad_ori < 0.0)
grad_ori += PI2;
while (grad_ori >= PI2)
grad_ori -= PI2;
double obin = grad_ori * (bins / PI2);
double weight = exp(conste*(rot_x*rot_x + rot_y * rot_y));
InterpHistEntry(hist, xbin, ybin, obin, grad_mag*weight, bins, width);
}
}
}
}
return hist;
}
void NormalizeDescr(Keypoint& feat)
{
double cur, len_inv, len_sq = 0.0;
int i, d = feat.descr_length;
for (i = 0; i < d; i++)
{
cur = feat.descriptor[i];
len_sq += cur*cur;
}
len_inv = 1.0 / sqrt(len_sq);
for (i = 0; i < d; i++)
feat.descriptor[i] *= len_inv;
}
/********************************************************************************************************************************
*模块说明:
* 模块七--步骤2:直方图到描述子的转换
*功能说明:
*
*********************************************************************************************************************************/
void HistToDescriptor(double ***hist, int width, int bins, Keypoint& feature)
{
int int_val, i, r, c, o, k = 0;
for (r = 0; r < width; r++)
for (c = 0; c < width; c++)
for (o = 0; o < bins; o++)
{
feature.descriptor[k++] = hist[r][c][o];
}
feature.descr_length = k;
NormalizeDescr(feature); //[1]描述子特征向量归一化
for (i = 0; i < k; i++) //[2]描述子向量门限
if (feature.descriptor[i] > DESCR_MAG_THR)
feature.descriptor[i] = DESCR_MAG_THR;
NormalizeDescr(feature); //[3]描述子进行最后一次的归一化操作
for (i = 0; i < k; i++) //[4]将单精度浮点型的描述子转换为整形的描述子
{
int_val = INT_DESCR_FCTR * feature.descriptor[i];
feature.descriptor[i] = min(255, int_val);
}
}
/********************************************************************************************************************************
*模块说明:
* 模块七:6 关键点描述
*功能说明:
* 1)通过以上步骤,对于一个关键点,拥有三个信息:位置、尺度、方向
* 2)接下来就是为每个关键点建立一个描述符,用一组向量来将这个关键点描述出来,使其不随各种变化而变化,比如光照、视角变化等等
* 3)这个描述子不但包括关键点,也包含关键点周围对其贡献的像素点,并且描述符应该有较高的独特性,以便于特征点正确的匹配概率
* 1)SIFT描述子----是关键点邻域高斯图像梯度统计结果的一种表示。
* 2)通过对关键点周围图像区域分块,计算块内梯度直方图,生成具有独特性的向量
* 3)这个向量是该区域图像信息的一种表述和抽象,具有唯一性。
*Lowe论文:
* Lowe建议描述子使用在关键点尺度空间内4*4的窗口中计算的8个方向的梯度信息,共4*4*8=128维向量来表征。具体的步骤如下所示:
* 1)确定计算描述子所需的图像区域
* 2)将坐标轴旋转为关键点的方向,以确保旋转不变性,如CSDN博文中的图6.2所示;旋转后邻域采样点的新坐标可以通过公式(6-2)计算
* 3)将邻域内的采样点分配到对应的子区域,将子区域内的梯度值分配到8个方向上,计算其权值
* 4)插值计算每个种子点八个方向的梯度
* 5)如上统计的4*4*8=128个梯度信息即为该关键点的特征向量。特征向量形成后,为了去除光照变化的影响,需要对它们进行归一化处理,
* 对于图像灰度值整体漂移,图像各点的梯度是邻域像素相减得到的,所以也能去除。得到的描述子向量为H,归一化之后的向量为L
* 6)描述子向量门限。非线性光照,相机饱和度变化对造成某些方向的梯度值过大,而对方向的影响微弱。因此,设置门限值(向量归一化
* 后,一般取0.2)截断较大的梯度值。然后,在进行一次归一化处理,提高特征的鉴别性。
* 7)按特征点的尺度对特征描述向量进行排序
* 8)至此,SIFT特征描述向量生成。
*********************************************************************************************************************************/
void DescriptorRepresentation(vector<Keypoint>& features, const vector<Mat>& gauss_pyr, int bins, int width)
{
double ***hist;
for (int i = 0; i < features.size(); i++)
{ //[1]计算描述子的直方图
hist = CalculateDescrHist(gauss_pyr[features[i].octave*(INTERVALS + 3) + features[i].interval],
features[i].x, features[i].y, features[i].octave_scale, features[i].ori, bins, width);
HistToDescriptor(hist, width, bins, features[i]); //[2]直方图到描述子的转换
for (int j = 0; j < width; j++)
{
for (int k = 0; k < width; k++)
{
delete[] hist[j][k];
}
delete[] hist[j];
}
delete[] hist;
}
}
bool FeatureCmp(Keypoint& f1, Keypoint& f2)
{
return f1.scale < f2.scale;
}
/*******************************************************************************************************************
*函数说明:
* 最大的模块1:SIFT算法模块
*函数参数说明:
* 1---const Mat &src---------------准备进行特征点检测的原始图片
* 2---vector<Keypoint>& features---用来存储检测出来的关键点
* 3---double sigma-----------------sigma值
* 4---int intervals----------------关键点所在的层数
********************************************************************************************************************/
void Sift(const Mat &src, vector<Keypoint>& features, double sigma, int intervals)
{
std::cout << "【Step_one】Create -1 octave gaussian pyramid image" << std::endl;
cv::Mat init_gray;
CreateInitSmoothGray(src, init_gray, sigma);
int octaves = log((double)min(init_gray.rows, init_gray.cols)) / log(2.0) - 2; //计算高斯金字塔的层数
std::cout << "【1】The height and width of init_gray_img = " << init_gray.rows << "*" << init_gray.cols << std::endl;
std::cout << "【2】The octaves of the gauss pyramid = " << octaves << std::endl;
std::cout << "【Step_two】Building gaussian pyramid ..." << std::endl;
std::vector<Mat> gauss_pyr;
GaussianPyramid(init_gray, gauss_pyr, octaves, intervals, sigma);
write_pyr(gauss_pyr, "gausspyramid");
std::cout << "【Step_three】Building difference of gaussian pyramid..." << std::endl;
vector<Mat> dog_pyr;
DogPyramid(gauss_pyr, dog_pyr, octaves, intervals);
write_pyr(dog_pyr, "dogpyramid");
std::cout << "【Step_four】Deatecting local extrema..." << std::endl;
vector<Keypoint> extrema;
DetectionLocalExtrema(dog_pyr, extrema, octaves, intervals);
std::cout << "【3】keypoints cout: " << extrema.size() << " --" << std::endl;
std::cout << "【4】extrema detection finished." << std::endl;
std::cout << "【5】please look dir gausspyramid, dogpyramid and extrema.txt.--" << endl;
std::cout << "【Step_five】CalculateScale..." << std::endl;
CalculateScale(extrema, sigma, intervals);
HalfFeatures(extrema);
std::cout << "【Step_six】Orientation assignment..." << std::endl;
OrientationAssignment(extrema, features, gauss_pyr);
std::cout << "【6】features count: " << features.size() << std::endl;
std::cout << "【Step_seven】DescriptorRepresentation..." << std::endl;
DescriptorRepresentation(features, gauss_pyr, DESCR_HIST_BINS, DESCR_WINDOW_WIDTH);
sort(features.begin(), features.end(), FeatureCmp);
cout << "finished." << endl;
}
/*******************************************************************************************************************
*函数说明:
* 画出SIFT特征点的具体函数
********************************************************************************************************************/
void DrawSiftFeature(Mat& src, Keypoint& feat, cv::Scalar color)
{
int len, hlen, blen, start_x, start_y, end_x, end_y, h1_x, h1_y, h2_x, h2_y;
double scl, ori;
double scale = 5.0;
double hscale = 0.75;
cv::Point start, end, h1, h2;
/* compute points for an arrow scaled and rotated by feat's scl and ori */
start_x = cvRound(feat.dx);
start_y = cvRound(feat.dy);
scl = feat.scale;
ori = feat.ori;
len = cvRound(scl * scale);
hlen = cvRound(scl * hscale);
blen = len - hlen;
end_x = cvRound(len * cos(ori)) + start_x;
end_y = cvRound(len * -sin(ori)) + start_y;
h1_x = cvRound(blen * cos(ori + CV_PI / 18.0)) + start_x;
h1_y = cvRound(blen * -sin(ori + CV_PI / 18.0)) + start_y;
h2_x = cvRound(blen * cos(ori - CV_PI / 18.0)) + start_x;
h2_y = cvRound(blen * -sin(ori - CV_PI / 18.0)) + start_y;
start = cv::Point(start_x, start_y);
end = cv::Point(end_x, end_y);
h1 = cv::Point(h1_x, h1_y);
h2 = cv::Point(h2_x, h2_y);
line(src, start, end, color, 1, 8, 0);
line(src, end, h1, color, 1, 8, 0);
line(src, end, h2, color, 1, 8, 0);
}
/*******************************************************************************************************************
*函数说明:
* 最大的模块3:画出SIFT特征点
********************************************************************************************************************/
void DrawSiftFeatures(Mat& src, vector<Keypoint>& features)
{
cv::Scalar color = CV_RGB(0, 255, 0);
for (int i = 0; i < features.size(); i++)
{
DrawSiftFeature(src, features[i], color);
}
}
/*******************************************************************************************************************
*函数说明:
* 最大的模块2:画出关键点KeyPoints
********************************************************************************************************************/
void DrawKeyPoints(Mat &src, vector<Keypoint>& keypoints)
{
int j = 0;
for (int i = 0; i < keypoints.size(); i++)
{
cv::Scalar color = { 255, 0 ,0 };
circle(src, Point(keypoints[i].dx, keypoints[i].dy), 3, color);
j++;
}
}
const char* GetFileName(const char* dir, int i)
{
char *name = new char[50];
sprintf(name, "%s\\%d\.jpg", dir, i);
return name;
}
void cv64f_to_cv8U(const Mat& src, Mat& dst)
{
double* data = (double*)src.data;
int step = src.step / sizeof(*data);
if (!dst.empty())
return;
dst.create(src.size(), CV_8U);
uchar* dst_data = dst.data;
for (int i = 0, m = 0; i < src.cols; i++, m++)
{
for (int j = 0, n = 0; j < src.rows; j++, n++)
{
*(dst_data + dst.step*j + i) = (uchar)(*(data + step*j + i) * 255);
}
}
}
//通过转换后保存的图像,会失真,和imshow显示出的图像相差很大
void writecv64f(const char* filename, const Mat& mat)
{
Mat dst;
cv64f_to_cv8U(mat, dst);
imwrite(filename, dst);
}
void write_pyr(const vector<Mat>& pyr, const char* dir)
{
for (int i = 0; i < pyr.size(); i++)
{
writecv64f(GetFileName(dir, i), pyr[i]);
}
}
void read_features(vector<Keypoint>&features, const char*file)
{
ifstream in(file);
int n = 0, dims = 0;
in >> n >> dims;
cout << n << " " << dims << endl;
for (int i = 0; i < n; i++)
{
Keypoint key;
in >> key.dy >> key.dx >> key.scale >> key.ori;
for (int j = 0; j < dims; j++)
{
in >> key.descriptor[j];
}
features.push_back(key);
}
in.close();
}
/*******************************************************************************************************************
*函数说明:
* 最大的模块4:将特征点写入文本文件
********************************************************************************************************************/
void write_features(const vector<Keypoint>&features, const char*file)
{
ofstream dout(file);
dout << features.size() << " " << FEATURE_ELEMENT_LENGTH << endl;
for (int i = 0; i < features.size(); i++)
{
dout << features[i].dy << " " << features[i].dx << " " << features[i].scale << " " << features[i].ori << endl;
for (int j = 0; j < FEATURE_ELEMENT_LENGTH; j++)
{
if (j % 20 == 0)
dout << endl;
dout << features[i].descriptor[j] << " ";
}
dout << endl;
}
dout.close();
}
main.cpp
/*************************************************************************************************************************
*文件说明:
* SIFT算法的实现
*开发环境:
* Win10+VS2012+OpenCv2.4.8
*时间地点:
* 陕西师范大学.文津楼 2016.12.30
*再次修改时间:
* 陕西师范大学.文津楼 2017.2.24
*作者信息:
* 九月
**************************************************************************************************************************/
#include <windows.h>
#include <iostream>
#include <opencv2/opencv.hpp>
#include <opencv2/highgui.hpp>
#include "sift.h"
using namespace std;
using namespace cv;
int main(int argc, char **argv)
{
cv::Mat src = imread("jobs_512.jpg");
if (src.empty())
{
cout << "jobs_512.jpg open error! " << endl;
getchar();
return -1;
}
if (src.channels() != 3) return -2;
vector<Keypoint> features;
Sift(src, features, 1.6); //【1】SIFT特征点检测和特征点描述
DrawKeyPoints(src, features); //【2】画出关键点(特征点)
DrawSiftFeatures(src, features); //【3】画出SIFT特征点
write_features(features, "descriptor.txt"); //【4】将特征点写入文本
cv::imshow("src", src);
cv::waitKey();
return 0;
}
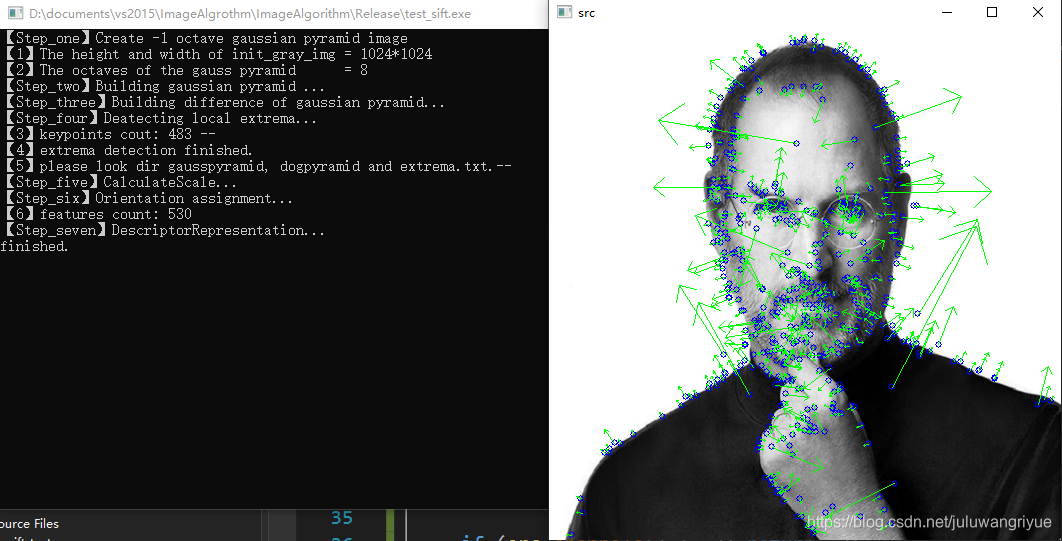
测试图片:

运行结果: