[人工智能]集成学习-数学基础

01
Metropolis-Hastings算法

import numpy as np
import random
import matplotlib.pyplot as plt

## 设置参数
mu = 0.5
sigma = 0.1
skip = 700  ## 设置收敛步长
num = 100000  ##采样点数

def Gussian(x,mu,sigma):
    return 1/(np.sqrt(2*np.pi)*sigma)*np.exp(-np.square((x-mu))/(2*np.square(sigma)))

def M_H(num):
    x_0 = 0
    samples = []
    j = 1
    while(len(samples) <= num):
        while True:
            x_1 = random.random()  # 转移函数(转移矩阵)
            q_i = Gussian(x_0,mu,sigma)
            q_j = Gussian(x_1,mu,sigma)
            alpha = min(1,q_i/q_j)
            u = random.random()
            if u <= alpha:
                x_0 = x_1
                if j >= skip:
                    samples.append(x_1)
                j = j + 1
                break
    return samples

norm_samples = M_H(num)

X = np.array(norm_samples)
px = Gussian(X,mu,sigma)
plt.scatter(X,px)
plt.show()

结果

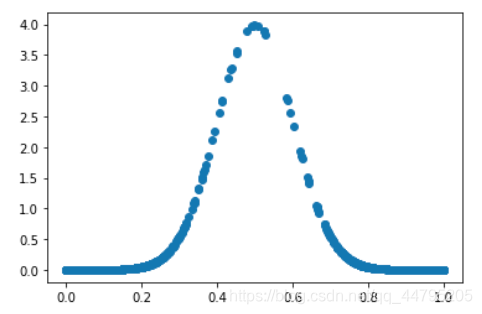
02
基础知识学习
2.1概率论与数理统计

# pi的估计问题
import numpy as np 
def pi_estimate(n):
    '''
    n为投点的数量
    '''
    n_rand_X = np.random.uniform(-1.0,1.0,n)
    n_rand_Y = np.random.uniform(-1.0,1.0,n)
    ## 判断是否在圆内
    distance = np.sqrt(n_rand_X**2 + n_rand_Y**2)
    dis_n = float(len(distance[distance<=1.0]))
    return 4 * (dis_n / n)

for i in [10,50,100,500,1000,5000,10000,50000,100000,500000,10000000]:
    print("pi的估计值为",pi_estimate(i))

# 电子元件寿命问题
import numpy as np 

def ele_life(n,c,h,t,lamb):
    """
    参数n:模拟实验的次数
    参数c:每次试验中的c个元件
    参数t:每c个元件中规定的合格品数量
    参数h:小时数
    """
    times = 0.0
    for i in range(n):
        c_rand = np.random.exponential(1/lamb,c)
        c_rand_t = len(c_rand[c_rand>h])
        if c_rand_t > t:
            times = times + 1
    return times / n  

ele_life(10000,1000,18,20,0.2)

# 三门问题
import numpy.random as random
def MontyHallProblem(n_test):
    #测试次数
     
    winning_door = random.randint(0,3,n_test)
    first_get  = 0
    change_get = 0
    for winning_doors in winning_door:
        act_door = random.randint(0,3)
        if winning_doors == act_door:
            first_get += 1
        else :
            change_get += 1
    first_pro  = first_get / n_test
    change_pro = change_get / n_test
    compar1    = round(change_get / first_get,2)
    print ("在%d次测试中,坚持原则第一次就选中的次数是%d,改变决定选择另一扇门中奖的次数是%d"% (n_test,first_get,change_get))
    print ("概率分别是{0}和{1}，改变决定选择另一扇门中奖几率是坚持选择的{2}倍".format(first_pro,change_pro,compar1))
MontyHallProblem(100000)

03
随机过程

import numpy as np 
import matplotlib.pyplot as plt
plt.style.use("ggplot")

# 模拟泊松过程
def poisson_process(n,lmd,times):
    ## n是模拟的次数,lmd是泊松过程的强度,times是每次模拟发生的次数
    fin_list = []
    y_list = []
    for i in range(n):
        mid_list = []
        mid_list_y = []
        y = 1
        for time in range(times):
            mid_ans = np.random.exponential(lmd)
            mid_list.append(mid_ans)
            mid_list_y.append(y)
            y = y+1
        y_list.append(mid_list_y)
        
        for p,mid in enumerate(mid_list):
            if p == 0:
                pass
            else:
                mid_list[p] = sum(mid_list[0:p+1])
        fin_list.append(mid_list)
    for li,y_li in zip(fin_list,y_list):
        li.insert(0,0)
        y_li.insert(0,0)
        plt.step(li,y_li)

## 开始模拟
poisson_process(10000,0.05,10)

04
高等数学

import numpy as np
import matplotlib.pyplot as plt


def f(x):
    return np.power(x, 2)

def d_f_1(x):
    '''
    求导数的方式1
    '''
    return 2.0 * x

def d_f_2(f, x, delta=1e-4):
    '''
    求导数的第二种方法
    '''
    return (f(x+delta) - f(x-delta)) / (2 * delta)


# plot the function
xs = np.arange(-10, 11)
plt.plot(xs, f(xs))


learning_rate = 0.1
max_loop = 30

x_init = 10.0
x = x_init
lr = 0.1
x_list = []
for i in range(max_loop):
    #d_f_x = d_f_1(x)
    d_f_x = d_f_2(f, x)
    x = x - learning_rate * d_f_x
    x_list.append(x)
x_list = np.array(x_list)
plt.scatter(x_list,f(x_list),c="r")
plt.show()

print('initial x =', x_init)
print('arg min f(x) of x =', x)
print('f(x) =', f(x))

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import time
%matplotlib inline
from mpl_toolkits.mplot3d import Axes3D
class Rosenbrock():
    def __init__(self):
        self.x1 = np.arange(-100, 100, 0.0001)
        self.x2 = np.arange(-100, 100, 0.0001)
        #self.x1, self.x2 = np.meshgrid(self.x1, self.x2)
        self.a = 1
        self.b = 1
        self.newton_times = 1000
        self.answers = []
        self.min_answer_z = []


    # 准备数据
    def data(self):
        z = np.square(self.a - self.x1) + self.b * np.square(self.x2 - np.square(self.x1))
        #print(z.shape)
        return z

    # 随机牛顿
    def snt(self,x1,x2,z,alpha):
        rand_init = np.random.randint(0,z.shape[0])
        x1_init,x2_init,z_init = x1[rand_init],x2[rand_init],z[rand_init]
        x_0 =np.array([x1_init,x2_init]).reshape((-1,1))
        #print(x_0)


        for i in range(self.newton_times):
            x_i = x_0 - np.matmul(np.linalg.inv(np.array([[12*x2_init**2-4*x2_init+2,-4*x1_init],[-4*x1_init,2]])),np.array([4*x1_init**3-4*x1_init*x2_init+2*x1_init-2,-2*x1_init**2+2*x2_init]).reshape((-1,1)))
            x_0 = x_i
            x1_init = x_0[0,0]
            x2_init = x_0[1,0]
        answer = x_0
        return answer


    # 绘图
    def plot_data(self,min_x1,min_x2,min_z):
        x1 = np.arange(-100, 100, 0.1)
        x2 = np.arange(-100, 100, 0.1)
        x1, x2 = np.meshgrid(x1, x2)
        a = 1
        b = 1
        z = np.square(a - x1) + b * np.square(x2 - np.square(x1))
        fig4 = plt.figure()
        ax4 = plt.axes(projection='3d')
        ax4.plot_surface(x1, x2, z, alpha=0.3, cmap='winter')  # 生成表面， alpha 用于控制透明度
        ax4.contour(x1, x2, z, zdir='z', offset=-3, cmap="rainbow")  # 生成z方向投影，投到x-y平面
        ax4.contour(x1, x2, z, zdir='x', offset=-6, cmap="rainbow")  # 生成x方向投影，投到y-z平面
        ax4.contour(x1, x2, z, zdir='y', offset=6, cmap="rainbow")  # 生成y方向投影，投到x-z平面
        ax4.contourf(x1, x2, z, zdir='y', offset=6, cmap="rainbow")  # 生成y方向投影填充，投到x-z平面，contourf()函数
        ax4.scatter(min_x1,min_x2,min_z,c='r')
        # 设定显示范围
        ax4.set_xlabel('X')
        ax4.set_ylabel('Y')
        ax4.set_zlabel('Z')
        plt.show()

    # 开始
    def start(self):
        times = int(input("请输入需要随机优化的次数："))
        alpha = float(input("请输入随机优化的步长"))
        z = self.data()
        start_time = time.time()
        for i in range(times):
            answer = self.snt(self.x1,self.x2,z,alpha)
            self.answers.append(answer)
        min_answer = np.array(self.answers)
        for i in range(times):
            self.min_answer_z.append((1-min_answer[i,0,0])**2+(min_answer[i,1,0]-min_answer[i,0,0]**2)**2)
        optimal_z = np.min(np.array(self.min_answer_z))
        optimal_z_index = np.argmin(np.array(self.min_answer_z))
        optimal_x1,optimal_x2 = min_answer[optimal_z_index,0,0],min_answer[optimal_z_index,1,0]
        end_time = time.time()
        running_time = end_time-start_time
        print("优化的时间:%.2f秒!" % running_time)
        self.plot_data(optimal_x1,optimal_x2,optimal_z)
if __name__ == '__main__':
    snt = Rosenbrock()
    snt.start()

05
线性代数
向量和矩阵计算

本次学习内容来源Datawhale组织