[人工智能]详解经典旋转目标检测算法RoI Transformer

一、引言

1、旋转目标检测检测就是将具有旋转方向的目标检测出来，也就是需要检测目标的中心点、长宽、角度。在俯视图的目标检测中比较常见，如遥感图像目标检测、航拍图像目标检测等。(见下图旋转目标检测，图源论文RoI Transformer )

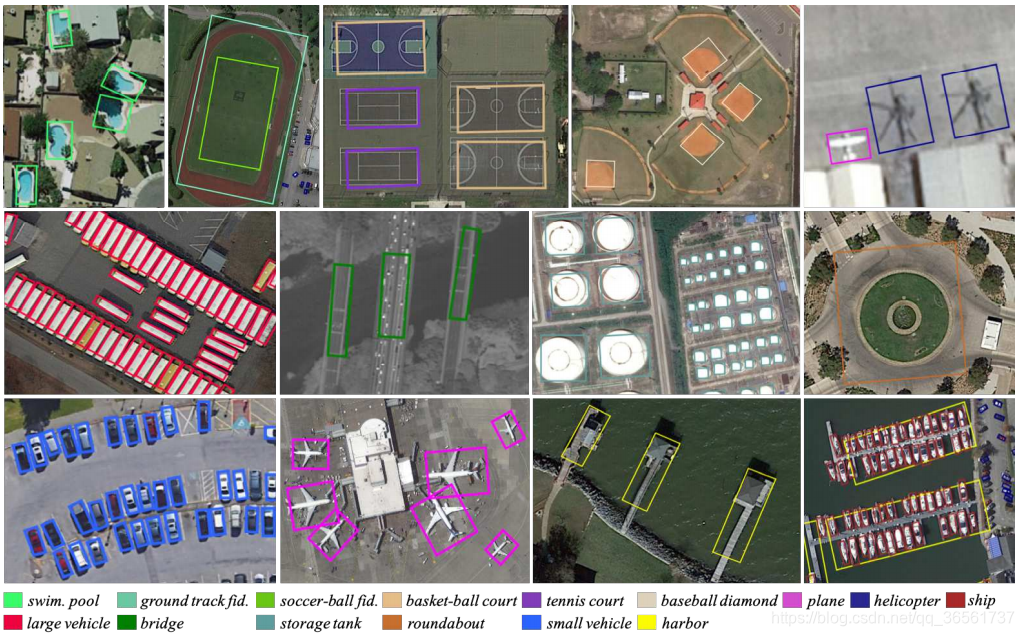
2、旋转目标检测算法，目前多阶段里面性能较好的是RoI Transformer这个算法，本篇博客将详细分析此算法。
论文《Learning RoI Transformer for Oriented Object Detection in Aerial Images》
开源代码基于mmdetection。
3、先简要看一下RoI Transformer的介绍吧，移步这里见第三部分旋转目标检测。
4、下面将从数据处理、网络结构、RoI Align三个方面进行介绍。

二、数据处理

常见的目标检测算法都是做的水平目标检测，预测目标的中心点、长宽就好了，那么旋转目标多了一个角度。对于不同的算法对于角度的定义不同，处理方式略微不同。下面主要介绍两种旋转目标检测角度定义的方式。
1、opencv旋转矩形角度定义方式
opencv在旋转矩形的时候，以X轴逆时针旋转θ角度得到宽边，表示旋转的角度，如图红色角度。因此所有的角度范围为[-90,0)

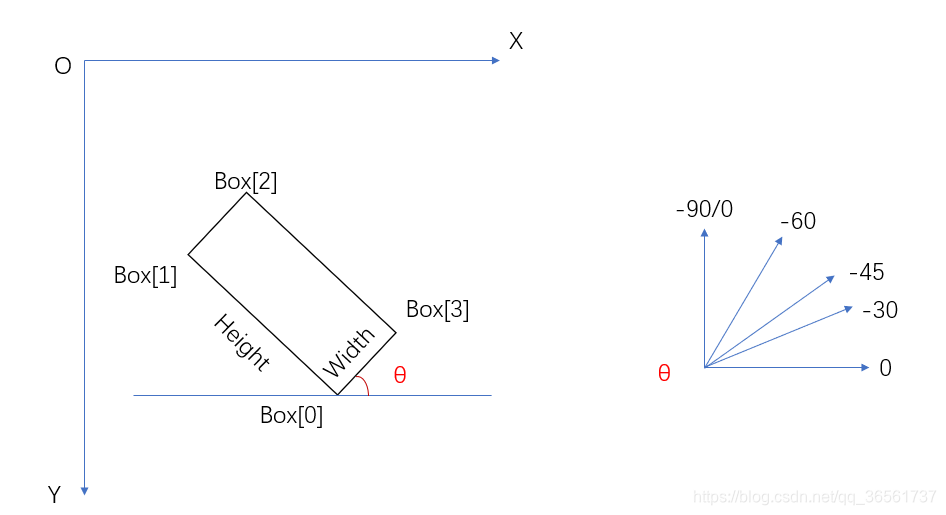
下面说下在用opencv如何得到旋转矩形的坐标及其角度。

img = cv2.imread('test.png') #读入rgb图像
gray = cv2.cvtColor(img,cv2.COLOR_BGR2GRAY) #转化为灰度图
ret, binary = cv2.threshold(gray,127,255,cv2.THRESH_BINARY)#获取二进制图像
#通过二进制图像获得二进制区域的边界框
#cv2.RETR_EXTERNAL表示只检测外轮廓
#cv2.CHAIN_APPROX_NONE存储所有的轮廓点
#返回值：img_是将轮廓部分画出来；contours所有轮廓坐标；hierarchy 表示轮廓属性，如个数等，具体可以查下opencv API
img_, contours, hierarchy = cv2.findContours(binary, cv2.RETR_EXTERNAL, cv2.CHAIN_APPROX_NONE)
max_contour = max(contours, key=len)
# 返回一个最小外接矩形 (x,y) (h,w),angle [-90,0)
rect = cv2.minAreaRect(max_contour)
#获得旋转矩形的四个顶点坐标
poly = cv2.boxPoints(rect)

2、RoI Transformer中旋转目标角度定义
论文中角度的定位范围是[-π，π]，针对bbox坐标[[x1,x2,x3,x4],[y1,y2,y3,y4]]，角度计算为θ=np.arctan2(-(x2-x1)，(y2-y1))，具体的角度见论文配图(如下)。

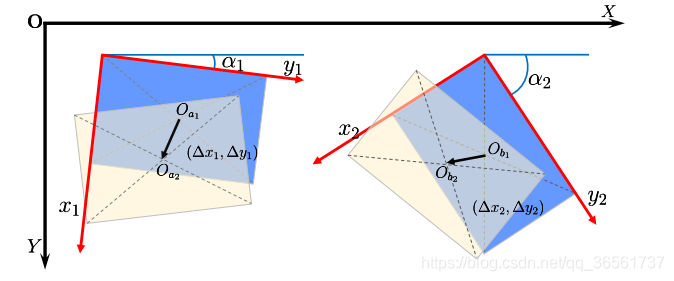
现在我们知道了角度的定义方式了，需要由八个顶点坐标计算中心点、长宽、θ这几个参数值。
(1)中心点计算
$(x,y)=(1/4{\sum }_i^4{x}_i，1/4{\sum }_i^4{y}_i)$
(2)长宽计算
长宽计算在此论文中先将旋转框经过角度旋转之后得到水平框，然后计算水平框的x、y坐标的左右、上下极值，得到[minx, miny, maxx, maxy]四个坐标，再计算矩形的长宽值。

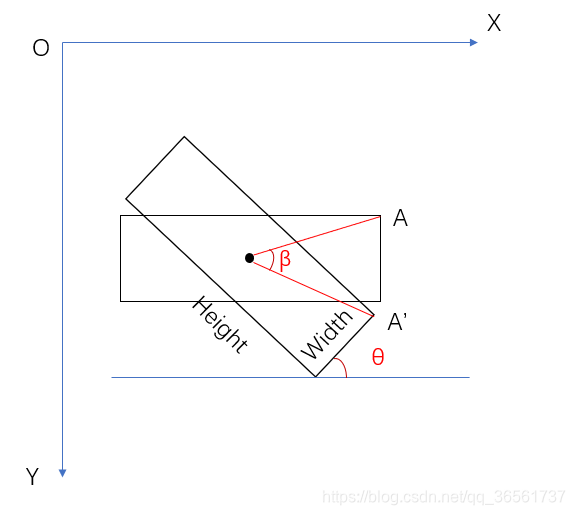
由图斜框与水平(x轴)的夹角是θ，那么将此斜框逆时针旋转β角度得到水平框。显然可得β=θ(可以自己证明一下，很简单)。那么现在就可以根据θ和A’点坐标来计算旋转之后点A的坐标了。
为了看起来简单，以斜框的中心点画坐标轴(因为四个坐标都可以以中心点作为参考)

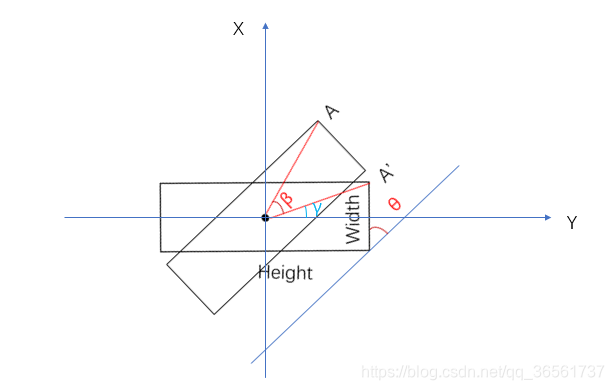
设A’坐标[x’,y’]，求A的坐标[x,y]，设红直线的长度为d(即A与A’到中心的距离)
$x=d\times sin(\beta +\gamma )=d\times (sin\beta cos\gamma +sin\gamma cos\beta )=x^{\prime }cos\beta +y^{\prime }sin\beta$
$y=d\times cos(\beta +\gamma )=d\times (cos\beta cos\gamma ?sin\beta sin\gamma )=y^{\prime }cos\beta ?x^{\prime }sin\beta$
3、RoI Transformer中标签处理过程
旋转矩形框标注一般都是四个点的八个坐标(x,y)，由于标注过程中存在很多误差，很多时候标注的并不是矩形，而是不规则四边形(比如图像边缘区域、密集小目标)，那么这个时候直接利用四个坐标去计算长宽、偏转角度是不合适的。在RoI Transformer中处理过程如下：
(1)由四个标注点得到四边形封闭mask(二值矩阵)；
(2)opencv通过mask找到最小外接矩形的四个点坐标(见1、opencv旋转矩形角度定义方式)；
(3)找到旋转矩形的最小外接水平矩形，计算旋转矩形与水平矩形的对应点(这个计算直接计算各对应点的距离，找到最小值)；比如最小外接水平矩形四个点为(A1、A2、A3、A4)，旋转矩形的四个顶点为(A1’、A2’、A3’、A4’)；
$mi{n}_d=min({\sum }_{i=1,2,3,4}|Ai?A{i}^{\prime }|,{\sum }_{i=2,3,4,1}|Ai?A{i}^{\prime }|,{\sum }_{i=3,4,1,2}|Ai?A{i}^{\prime }|,{\sum }_{i=4,1,2,3}|Ai?A{i}^{\prime }|)$
其中$|Ai?A{i}^{\prime }|$表示两个点的距离。
(4)这样找到了最佳对应点之后，再通过(2、RoI Transformer中旋转目标角度定义)得到旋转矩形的中心点、长宽、角度，即[cx,cy,w,h,θ]。
为什么要经过第3步找到旋转矩形与水平矩形的对应点呢？这里有两个原因：
(1)找到对应的起始点之后，计算θ就是一个确定值(2中角度计算方式$\theta =np.arctan2(?(x2?x1)，(y2?y1))$);
(2)找到旋转矩形与水平矩形最小的旋转角度，便于后续通过水平Anchor预测旋转矩形。

三、网络结构

网络结构部分整体类似一个cascade rcnn，过程是BackBone->RPN->rbbox1->rbbox2。

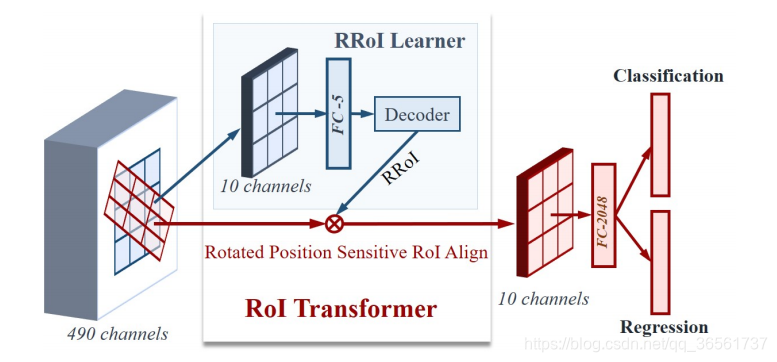
1、图像先经过Backbone进行特征提取(FPN略去)
这里用的ResNet系列网络，可以替换成ResNeXt、ResNeSt等Backbone。
2、经过RPN网络得到水平proposal

# RPN网络结构，rpn_conv表示共享层，然后分别进行cls和reg预测
rpn_conv = nn.Conv2d(in_channels, feat_channels, 3, padding=1) #共享层
rpn_cls = nn.Conv2d(feat_channels,num_anchors * cls_out_channels, 1) #cls，num_anchor表示同一层特征中同一个位置有几个Anchorc尺寸比例，一般是3(0.5,1,2)
rpn_reg = nn.Conv2d(feat_channels, num_anchors * 4, 1) # *4表示[delta_x,delta_y,delta_w,delya_h]

这个过程就是普通的RPN网络，将RPN网络中cls分支按照得分进行排序，取最高的前K个；然后得到这K个得分对应的bbox偏差预测(检测头输出结果)，与对应的K个Anchor进行偏差回归得到K个预测框，然后再进行NMS。
3、由水平proposal经过RoI Align得到水平proposal的特征
就是普通的RoI Align
4、对proposal特征进行分类和回归得到旋转矩形框(rbbox1)
回归输出五个值，包括中心点位置、长宽、角度，其中这里的角度是相对于水平proposal的旋转的角度(其实也就是ground truth的角度，因为proposal也是水平的，所以角度是一样的)；
5、由rbbox1经过RRoI Align得到旋转矩形框的特征；
6、由rbbox1的特征，再次经过分类和回归头得到最终的旋转矩形rbbox2
(这里的中心点、长宽、角度偏移都是相对于rbbox1的偏移)。

四、RRoI Align(旋转RoI Align)