[人工智能]Towards Certifying L_Infinity Robustness using Neural Networks with L_Infinity-dist Neurons

这是一篇解决对抗稳定性的顶会(ICML2021)文章。

摘要
现有的神经网络对输入的扰动较敏感，这对于神经网络的应用很不友好，如何对抗这种鲁棒性具有重要的价值。作者认为，现有网络设计必然导致这种不稳定性，稳定的函数具有Lipschitz性质。因此，作者重新设计了神经网络的forward操作，使得神经网络保持Lipschitz性，从而对抗神经网络的不稳定。

贡献

• 在网络层面对抗稳定性，使得网络具有Lipschitz性质
• 重新设计了$L_{\infty }$距离神经元，并克服了网络训练中的一些困难
• 理论证明了这种网络可以逼近任意常数为1的Lipschitz函数

Lipschitz

对于函数$f(x)$，对于任意的取值$x_1,x_2$，存在一个常数$\lambda$，满足
$$||f(x_1)?f(x_2)|{|}_p\le \lambda ||x_1?x_2|{|}_p$$
就说函数$f(x)$是关于$l_p$范数的$\lambda ?Lipschitz$函数。

$L_{\infty }?dist$ 神经网络

通过如下的转化，重新定义了一个神经元之间的传播关系。其他和常规的神经网络类似。

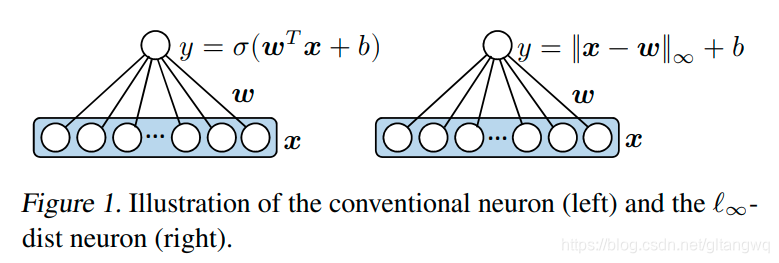
详细内容请看原论文。