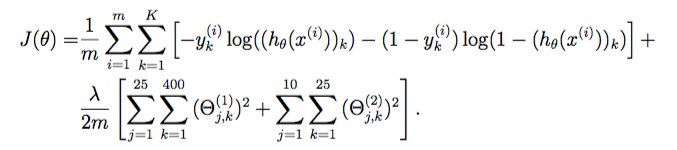[人工智能]吴恩达机器学习作业（四）——BP神经网络--Python实现

BP神经网络，即使用反向传播算法（BackPropagation algorithm）的神经网络

参考
以下为python语言实现的反向传播算法

import numpy as np
from scipy.io import loadmat
from scipy.optimize import minimize
from sklearn.preprocessing import OneHotEncoder
import scipy.io as scio


def load_data(path, transpose=True):
    data = loadmat(path)
    y = data.get('y')  # (5000,1)

    X = data.get('X')  # (5000,400)

    if transpose:
        # for this dataset, you need a transpose to get the orientation right
        X = np.array([im.reshape((20, 20)).T for im in X])

        # and I flat the image again to preserve the vector presentation
        X = np.array([im.reshape(400) for im in X])

    return X, y

def sigmoid_gradient(z):
    return np.multiply(sigmoid(z), (1 - sigmoid(z)))


def sigmoid(z):  # sigmoid的导函数
    return 1 / (1 + np.exp(-z))


def forward_propagate(X, theta1, theta2):
    m = X.shape[0]  # m = 5000
    a1 = np.insert(X, 0, values=np.ones(m), axis=1)  # input layer
    z2 = a1 * theta1.T
    a2 = np.insert(sigmoid(z2), 0, values=np.ones(m), axis=1)  # hidden layer
    z3 = a2 * theta2.T
    h = sigmoid(z3)  # h.shape(5000,10)
    return a1, z2, a2, z3, h


def cost(params, input_size, hidden_size, num_labels, X, y, learning_rate):
    m = X.shape[0]  # 5000,input_size = 400+1; hidden_size = 25+1
    X = np.mat(X)
    y = np.mat(y)

    # reshape the parameter array into parameter matrices for each layer
    theta1 = np.mat(np.reshape(params[:hidden_size * (input_size + 1)], (hidden_size, (input_size + 1))))
    # params未指定起始位置，默认从零开始，其中params为theta一共的个数，[:25*(400+1)]reshape为(25,400+1)的矩阵格式
    theta2 = np.mat(np.reshape(params[hidden_size * (input_size + 1):], (num_labels, (hidden_size + 1))))
    # params中剩下的为theta2中的值
    # run the feed-forward pass
    a1, z2, a2, z3, h = forward_propagate(X, theta1, theta2)

    # compute the cost
    J = 0
    for i in range(m):  # m = 5000,multiply为点乘
        first_term = np.multiply(-y[i, :], np.log(h[i, :]))  # h.shape 为 5000，10
        second_term = np.multiply((1 - y[i, :]), np.log(1 - h[i, :]))
        J += np.sum(first_term - second_term)
    J = J / m
    # add the cost regularization term
    J += (float(learning_rate) / (2 * m)) * (np.sum(np.power(theta1[:, 1:], 2)) + np.sum(np.power(theta2[:, 1:], 2)))
    return J


def backprop(params, input_size, hidden_size, num_labels, X, y, learning_rate):
    m = X.shape[0]
    X = np.mat(X)
    y = np.mat(y)

    # reshape the parameter array into parameter matrices for each layer
    theta1 = np.mat(np.reshape(params[:hidden_size * (input_size + 1)], (hidden_size, (input_size + 1))))
    theta2 = np.mat(np.reshape(params[hidden_size * (input_size + 1):], (num_labels, (hidden_size + 1))))

    # run the feed-forward pass
    a1, z2, a2, z3, h = forward_propagate(X, theta1, theta2)

    # initializations
    J = 0
    delta1 = np.zeros(theta1.shape)  # (25, 401)
    delta2 = np.zeros(theta2.shape)  # (10, 26)

    # compute the cost
    for i in range(m):
        first_term = np.multiply(-y[i, :], np.log(h[i, :]))
        second_term = np.multiply((1 - y[i, :]), np.log(1 - h[i, :]))
        J += np.sum(first_term - second_term)

    J = J / m

    # add the cost regularization term
    J += (float(learning_rate) / (2 * m)) * (np.sum(np.power(theta1[:, 1:], 2)) + np.sum(np.power(theta2[:, 1:], 2)))

    # perform backpropagation
    for t in range(m):
        a1t = a1[t, :]  # (1, 401)
        z2t = z2[t, :]  # (1, 25)
        a2t = a2[t, :]  # (1, 26)
        ht = h[t, :]  # (1, 10)
        yt = y[t, :]  # (1, 10)

        d3t = ht - yt  # (1, 10)
        # 详见吴恩达机器学习笔记P135页，反向传播算法的过程
        z2t = np.insert(z2t, 0, values=np.ones(1))  # (1, 26)
        d2t = np.multiply((theta2.T * d3t.T).T, sigmoid_gradient(z2t))  # (1, 26)

        delta1 = delta1 + (d2t[:, 1:]).T * a1t
        delta2 = delta2 + d3t.T * a2t

    delta1 = delta1 / m  # 计算0时
    delta2 = delta2 / m

    # add the gradient regularization term
    delta1[:, 1:] = delta1[:, 1:] + (theta1[:, 1:] * learning_rate) / m  # 计算非零时
    delta2[:, 1:] = delta2[:, 1:] + (theta2[:, 1:] * learning_rate) / m

    # unravel the gradient matrices into a single array
    grad = np.concatenate((np.ravel(delta1), np.ravel(delta2)))
    # axis=0 按照行拼接。默认为axis=0
    # axis=1 按照列拼接
    return J, grad


X, y = load_data('ex4data1.mat')
encoder = OneHotEncoder(sparse=False)
y_onehot = encoder.fit_transform(y)
input_size = 400
hidden_size = 25
num_labels = 10
learning_rate = 1
# 随机初始化完整网络参数大小的参数数组
params = (np.random.random(size=hidden_size * (input_size + 1) + num_labels * (hidden_size + 1)) - 0.5) * 0.25
# np.random.random(n)产生n个0--1之间的随机数,上式中产生的随机数为-0.5到0.5再*0.25
# 一共产生了，25*（400+1）+10*（25+1）个（theta的总个数）


theta1 = np.mat(np.reshape(params[:hidden_size * (input_size + 1)], (hidden_size, (input_size + 1))))
theta2 = np.mat(np.reshape(params[hidden_size * (input_size + 1):], (num_labels, (hidden_size + 1))))
fmin = minimize(fun=backprop, x0=params, args=(input_size, hidden_size, num_labels, X, y_onehot, learning_rate),
                method='TNC', jac=True, options={'maxiter': 250})


X = np.mat(X)
theta1 = np.mat(np.reshape(fmin.x[:hidden_size * (input_size + 1)], (hidden_size, (input_size + 1))))
theta2 = np.mat(np.reshape(fmin.x[hidden_size * (input_size + 1):], (num_labels, (hidden_size + 1))))

a1, z2, a2, z3, h = forward_propagate(X, theta1, theta2)
y_pred = np.array(np.argmax(h, axis=1) + 1)
correct = [1 if a == b else 0 for (a, b) in zip(y_pred, y)]
accuracy = (sum(map(int, correct)) / float(len(correct)))
print('accuracy = {0}%'.format(accuracy * 100))
scio.savemat('theta1.mat', {'theta1': theta1})
scio.savemat('theta2.mat', {'theta2': theta2})
print('保存成功')

最后三行代码我们将训练好的参数保存为mat文件，方便测试使用。使用该算法时，准确率达到了99%多一点，但毕竟训练和测试用的同一数据集该准确率肯定是偏高的，比上一个练习中回归模型的准确率好很多。依然秉承着严谨的态度，对训练好的模型进性测试。微软雅黑对了7个，手写对了4个。果然还是不太聪明的样子。

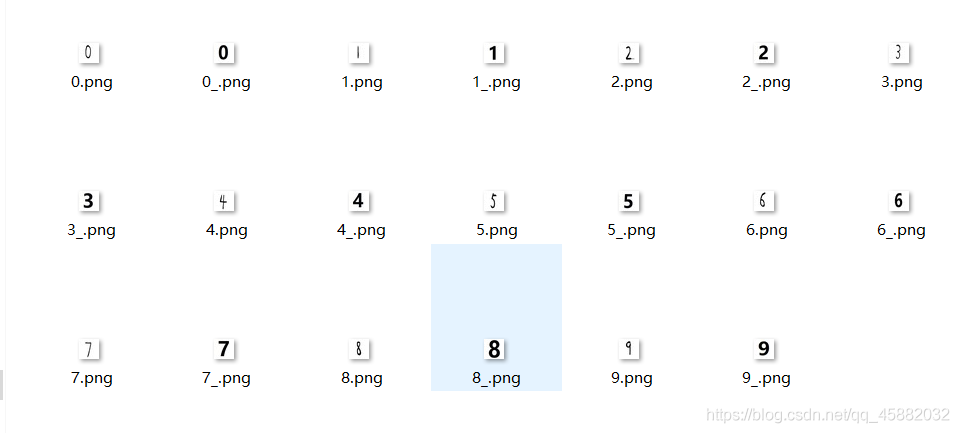
图片保存在名为img的文件下

import numpy as np
from scipy.io import loadmat
from PIL import Image


def sigmoid(z):
    return 1 / (1 + np.exp(-z))


def forward_propagate(X, theta1, theta2):
    m = X.shape[0]  # m = 5000
    a1 = np.insert(X, 0, values=np.ones(m), axis=1)  # input layer
    z2 = a1 * theta1.T
    a2 = np.insert(sigmoid(z2), 0, values=np.ones(m), axis=1)  # hidden layer
    z3 = a2 * theta2.T
    h = sigmoid(z3)  # h.shape(5000,10)
    return a1, z2, a2, z3, h


for i in range(10):
    filename = 'image/'+str(i)+'_.png'
    im = 255 - np.array(Image.open(filename).convert('L'))  # 为灰度图像，每个像素用8个bit表示，0表示黑，255表示白，

    im = im.ravel()
    im = im.astype(float) / 255.0

    theta1 = loadmat('theta1.mat')
    theta1 = theta1['theta1']

    theta2 = loadmat('theta2.mat')
    theta2 = theta2['theta2']

    im = np.mat(im)
    im2 = np.insert(im, 0, values=np.ones(1), axis=1)
    a1, z2, a2, z3, h = forward_propagate(im, theta1, theta2)
    answer = np.argmax(h) + 1
    if answer == 10:
        answer = 0
    print(" i think this should be " + str(answer))

上次模型中训练用的数据是直接用的，这次将所有数据转化为正面图像后再进性的训练。所以第二个测试代码中并未镜像处理。仅灰度变化就可。

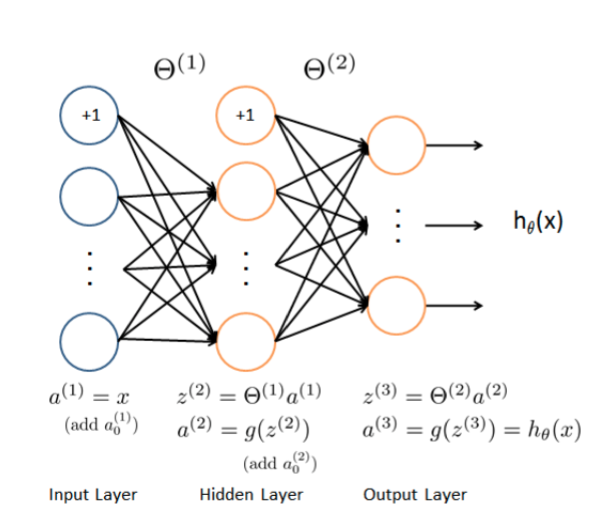
模型直观图：
该模型输入层有（100+1）
中间层（25+1）
输出层（10）

损失函数（正则化）：