实验目的
1、理解等高线的几何含义、如何发现一个函数的最小解；
掌握一门绘制函数图形的编程工具；
实验内容
给定下述Rosenbrock函数，f(x)=(a-x1)*2+b(x2-x1*x1)**2。试编写程序完成下述工作：
1）为不同的a,b取值，绘制该函数的3D表面。请问 a,b取值对该表面形状有大的影响吗？，所谓大影响就是形状不再相似。对a,b的取值区间，能否大致给出一个分类，像下面这样给出一张表：
| b=[b1,b2] | b=[b3,b4] | … | |
|---|---|---|---|
| a=[a1,a2] | |||
| a=[a3,a4] | |||
| … |
# 用matplotlib模块的三维模块来绘制
import numpy as np
import matplotlib.pyplot as plt
import random
from mpl_toolkits.mplot3d import Axes3D
fig = plt.figure()
ax = fig.gca(projection='3d')
# prepare data
x = np.arange(-100, 100, 0.5)
y = np.arange(-100, 100, 0.5)
x, y = np.meshgrid(x, y)
a=10000000000
b=10000000000
z = np.square(a-x) + b*np.square(y - x**2)
surf = ax.plot_surface(x, y, z, cmap='rainbow')
fig.colorbar(surf, shrink=0.5, aspect=5)
plt.show()
通过设置不同的：a和b的值来查看图形的变化情况
1:a=0,b=0
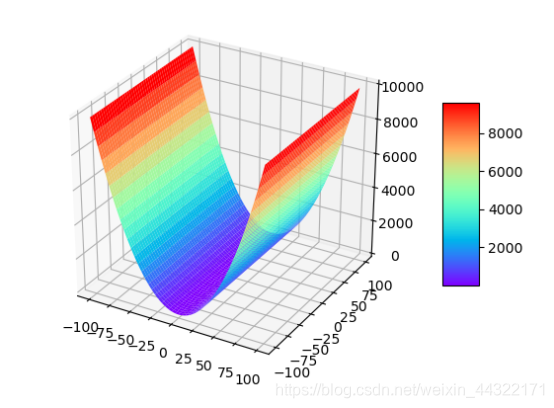
2:a=0,b=-1
3:a=10,b=10
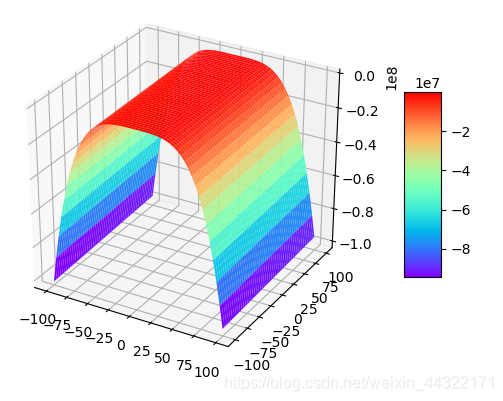
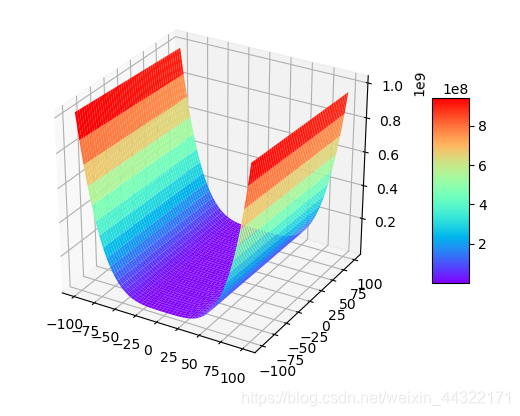4:a=-10,b=-10
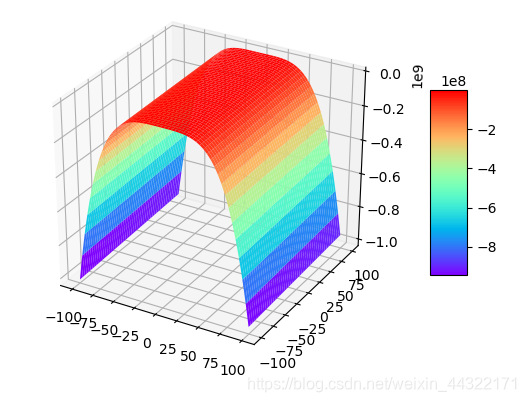5:a=1,b=1000000000
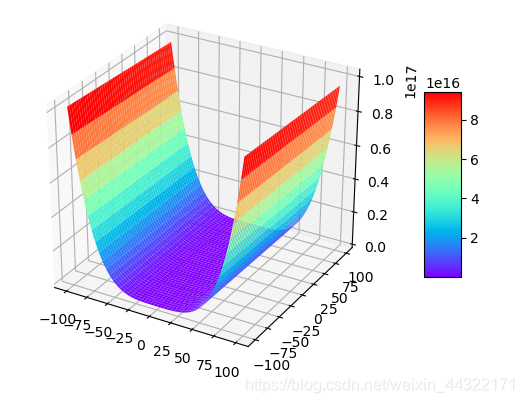6:a=1000000000,b=1
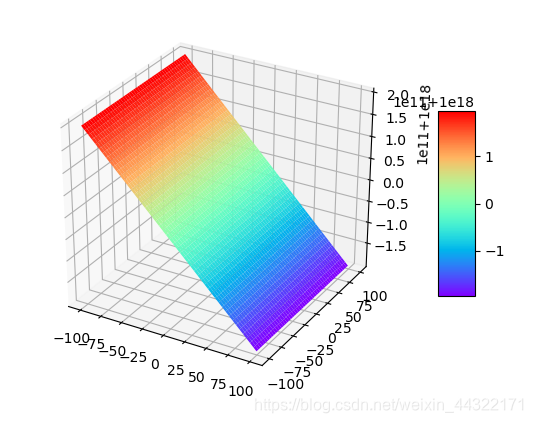7:a=-100000000,b=1
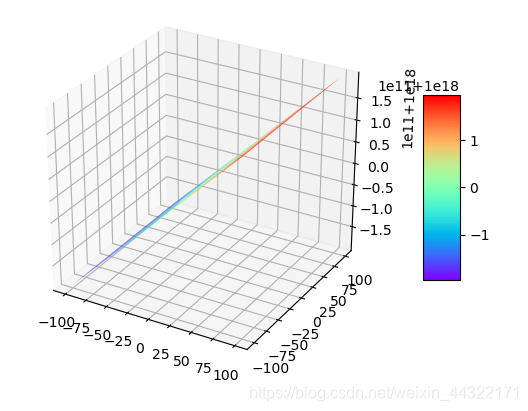
对比可以发现
1：b的取值正负对图形起着反翻转的作用
2：a取值的正负对图形无太多影响
3：当a的取值为b的万倍级以上时候对图形起着拉伸的作用
4：b的倍数无太大关系，只与正负有关
2）编写一个算法来找到它的全局最小值及相应的最小解，并在3D图中标出。分析一下你的算法时空效率、给出运行时间。
牛顿法和梯度下降法的比较
1.牛顿法：是通过求解目标函数的一阶导数为0时的参数，进而求出目标函数最小值时的参数。收敛速度很快。
海森矩阵的逆在迭代过程中不断减小，可以起到逐步减小步长的效果。缺点：海森矩阵的逆计算复杂，代价比较大，因此有了拟牛顿法。
2.梯度下降法：是通过梯度方向和步长，直接求解目标函数的最小值时的参数。
越接近最优值时，步长应该不断减小，否则会在最优值附近来回震荡。
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import time
%matplotlib inline
from mpl_toolkits.mplot3d import Axes3D
class Rosenbrock():
def __init__(self):
self.x1 = np.arange(-100, 100, 0.0001)
self.x2 = np.arange(-100, 100, 0.0001)
#self.x1, self.x2 = np.meshgrid(self.x1, self.x2)
self.a = 1
self.b = 1
self.newton_times = 1000
self.answers = []
self.min_answer_z = []
# 准备数据
def data(self):
z = np.square(self.a - self.x1) + self.b * np.square(self.x2 - np.square(self.x1))
#print(z.shape)
return z
# 随机牛顿
def snt(self,x1,x2,z,alpha):
rand_init = np.random.randint(0,z.shape[0])
x1_init,x2_init,z_init = x1[rand_init],x2[rand_init],z[rand_init]
x_0 =np.array([x1_init,x2_init]).reshape((-1,1))
#print(x_0)
for i in range(self.newton_times):
x_i = x_0 - np.matmul(np.linalg.inv(np.array([[12*x2_init**2-4*x2_init+2,-4*x1_init],[-4*x1_init,2]])),np.array([4*x1_init**3-4*x1_init*x2_init+2*x1_init-2,-2*x1_init**2+2*x2_init]).reshape((-1,1)))
x_0 = x_i
x1_init = x_0[0,0]
x2_init = x_0[1,0]
answer = x_0
return answer
# 绘图
def plot_data(self,min_x1,min_x2,min_z):
x1 = np.arange(-100, 100, 0.1)
x2 = np.arange(-100, 100, 0.1)
x1, x2 = np.meshgrid(x1, x2)
a = 1
b = 1
z = np.square(a - x1) + b * np.square(x2 - np.square(x1))
fig4 = plt.figure()
ax4 = plt.axes(projection='3d')
ax4.plot_surface(x1, x2, z, alpha=0.3, cmap='winter') # 生成表面， alpha 用于控制透明度
ax4.contour(x1, x2, z, zdir='z', offset=-3, cmap="rainbow") # 生成z方向投影，投到x-y平面
ax4.contour(x1, x2, z, zdir='x', offset=-6, cmap="rainbow") # 生成x方向投影，投到y-z平面
ax4.contour(x1, x2, z, zdir='y', offset=6, cmap="rainbow") # 生成y方向投影，投到x-z平面
ax4.contourf(x1, x2, z, zdir='y', offset=6, cmap="rainbow") # 生成y方向投影填充，投到x-z平面，contourf()函数
ax4.scatter(min_x1,min_x2,min_z,c='purple', s=50, marker='D')
# 设定显示范围
ax4.set_xlabel('X')
ax4.set_ylabel('Y')
ax4.set_zlabel('Z')
plt.show()
# 开始
def start(self):
times = int(input("请输入需要随机优化的次数："))
alpha = float(input("请输入随机优化的步长"))
z = self.data()
start_time = time.time()
for i in range(times):
answer = self.snt(self.x1,self.x2,z,alpha)
self.answers.append(answer)
min_answer = np.array(self.answers)
for i in range(times):
self.min_answer_z.append((1-min_answer[i,0,0])**2+(min_answer[i,1,0]-min_answer[i,0,0]**2)**2)
optimal_z = np.min(np.array(self.min_answer_z))
optimal_z_index = np.argmin(np.array(self.min_answer_z))
optimal_x1,optimal_x2 = min_answer[optimal_z_index,0,0],min_answer[optimal_z_index,1,0]
end_time = time.time()
running_time = end_time-start_time
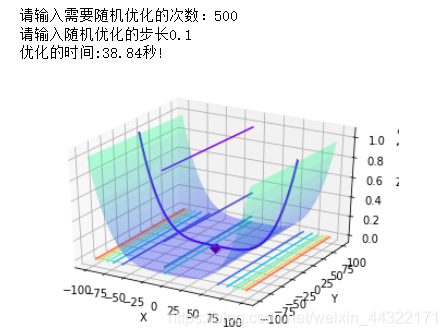
print("优化的时间:%.2f秒!" % running_time)
self.plot_data(optimal_x1,optimal_x2,optimal_z)
if __name__ == '__main__':
snt = Rosenbrock()
snt.start()
结果如下：
