[人工智能]李宏毅机器学习笔记——13. Explainable ML（可解释的机器学习）

摘要： 本章学习了Explainable ML，即我们不仅要会用机器学习，还要让机器学习具有可解释性。解释原因主要是为了使用者的需求，而不是为了完全理解model是如何工作的。

先是介绍了可解释的机器学习的分类：局部可解释性与全局可解释性。
局部可解释性：先讲解它的基本思想，然后应用移除组成要素（遮挡法）与 改变组成元素（基于梯度计算与显著图）的两种实现方法。

全局可解释性：在CNN中就通过反向寻找理想输入（寻找哪样的输入会使得结果最显著），与用添加正则化去提高机器所认为的结果图片的样子。基本思想是用一个容易解释的model去模仿不能解释的model的局部或者全部行为(一般是局部行为)，然后用容易解释的model解释该行为。比如线性模型与较简单的决策树。

1. Explainable machine learning的分类

机器不仅要告诉我们结果是什么，而且告诉我们判断理由是什么？

Explainable machine learning分为两种：

• 1.local explanation
  解释计算机为什么觉得这张图片是一只猫？

• Global Explainable
  解释在计算机眼中猫是什么样子的？

2. Why we need Explainable ML?

我们需要知道ML判别理由是什么，像用机器判断履历的时候，你得知道它是根据什么判断的，是具体能录呢还是性别等。
并且我们不仅需要机器结果的精确度，还需要进行模型诊断，看机器学习得怎么样；虽然有的任务精确度很高，但实际上有些机器什么都没学到，有了模型诊断后，我们就可以根据模型诊断的结果再来调整我们的模型。

个人观点

1. 可解释的ML并不等于完全理解ML是如何工作的，完全了解一个模型并不是必要的
2. 可解释的ML的目的是为了满足使用者的需求。
3. 对于不同的人，提供给不同的解释。

可解释性和能力的对比

有些模型可解释性强，比如线性模型，但是不够powerful。而DNN相当于一个黑盒子，虽然能力强于线性模型，但缺乏可解释性。所以我们的目标不是直接选择可解释性好的模型，而是让能力强的模型具有更好的解释性。
同时具有强大能力和可解释性的，是decision tree（决策树）。但实际上决策树结构如果很复杂(比如森林)，那么可解释性也会很差。（一般情况下decision tree也不好解释）

基于生物分类的关于decision tree的案例：

3. Local Explanation（局部可解释性）

3.1 基本思想

输入一个对象 x，由N个component 组成，我们想要知道，这N个component 中哪些对于识别图片起到关键作用。

• 图像来说，一个元素就是像素或者图像碎片
• 文章来说，一个元素就是单词

我们想要知道机器如何判断，这个问题其实等价于，机器把那些feature看的很重要，是这些feature的出现很大程度的影响了机器的判断。

那我们要做的就是，把我们的这些组成部分来进行修改或者移除等等，来查看影响的效果即可，如果影响比较大，那这些组成部分对机器识学习的判断结果有重要作用。基本思想如下图所示:

下面我们就分别使用移除和修改两种不同的操作来进行实验举例

3.2 移除组成要素（遮挡法）

在图像中的组成要素其实我们大致就可以看作是“一块区域”，这也是CNN的基本假设。那我们就可以移除一部分，然后来记录移除这个部分的影响。如下图，用灰色方块对图片中的每个部分依次进行遮挡，然后再进行预测，预测的效果在图的下方，与上图涂灰区域的中心对应，观察对识别结果的影响。
上图中蓝色区域说明此处的图像对图片识别起到重要作用。

例如上面第三张图中，机器识别出来了狗。如果我们不采用这种方法，我们完全可以不信机器真的是看到了狗才识别出来的，而是把左边的人看成了狗；而采用这种方法，我们看出如果图片中抹去了狗的部分，那机器完全不会在这张图中找到狗，那就说明了机器确实是学到了狗的相关特征。

注意：为什么要选择一个正方形区域？为什么选择变为灰色？如何选择区域的大小？

3.3 改变组成要素（基于Gradient）

从另一个角度来去寻找机器更看重哪些信息。对于比较重要的信息，按道理更有可能是对最后的结果影响越大，那么相当于就是，如果输入信息有改变，那么对结果的改变就会更大；如果我们把这个思想取极限，那么就是导数了。根据每个值对目标值得偏微分，我们可以画出一个Saliency Map（显著图）。

如上图，导数越大的地方越明亮。用Gradient 方式去判断哪些feature重要，哪些不重要的方法有很多种。

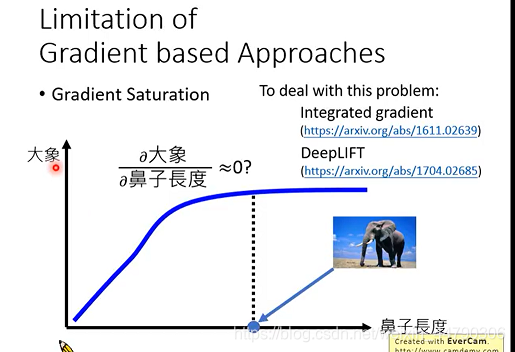
3.4 Limitation of Gradient based Approaches(基于梯度方式的限制）

梯度饱和（Gradient Saturation）
但这种方法存在一个比较大的问题，那就是信息冗余现象，如下图所示，横轴是鼻子长度，而纵轴是判断为大象的概率。显然，鼻子长是大象的一个极其显著的特点，这里的曲线我们也可以确定机器是关注到这一点的了；但是鼻子长到足够明显了的时候，再长貌似就没有必要了，即信息冗余。如果我们在这个时候看梯度，那竟然几乎是0，也就是梯度饱和，从而和我们的想法相矛盾，显然这是不合理的。

3.5 Attack Interpretation

使用Explainable技术时要注意有被攻击的风险，使用时要小心，有可能会被恶意攻击。

基于梯度与使用两种方法绘制saliency map（显著图）时，如上图所示，我们就加入了一些肉眼看不到的噪声，也没有改变机器分类的结果，但机器所关注到的部分改变了很多，例如上图中遭受攻击后，机器其实是通过看云来识别出了卡车。虽然我们无法解释这是为什么，但它确实发生了，这就说明了这种方法并不是完全可靠的，而且机器学到的内容可能还是很杂，不是我们想要的效果。

4. Global Explanation（全局可解释性）

解释回答在计算机眼中猫是什么样子的？
基本思路：当模型输出某一类别的可能的概率值最大时候，输入长什么样子？

4.1 反向寻找理想输入

在CNN中，我们就提到了全局可解释性。假设我们是在识别MNIST数据集的手写数字，我们既然是想知道在机器眼中，每个数字的样子，那我们就完全可以把结果固定，然后对输入通过梯度下降来得出，到底哪样的输入会使得结果最显著。
假设我们已经训练好了NN，并且已经给定了yi,那么global explanation要做的就是找到x*, x*=argmax?（yi）, x*需要满足让yi越大越好。

4.2 添加正则化项

我们其实是希望，我们最后生成的这些图片，不仅是找到$x?$可以得到$y^i$最大化，而且图片应该尽量像数字，从而这就添加了正则化项。

比如下图中左侧我们看到，白色像素的点还是太多了，而所有的手写数字图片中，白色的亮点都是比较少的，因此我们就可以在这里加入正则化项，使得我们的整体越暗越好，最后的结果如下图右侧所示，还是有一定效果的。（人为想的function去正则化）

4.3 利用image generator 进行正则化

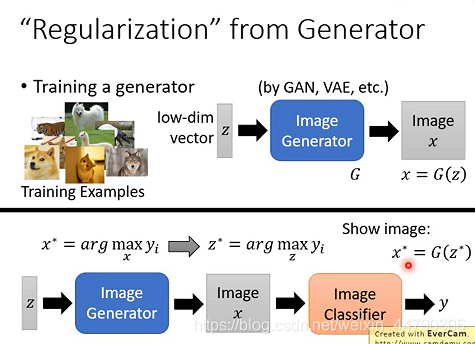
1. 首先训练一个image generator（通过GAN，VAE等生成模型），其输入一个低维度的向量z（不同的z代表不同的种类），输出一张图片 x ，记为X=G（z）。
2. 将x进行图片分类可以得到y。在之前方法中，想要得到机器眼中y的样子，就是计算X*=argmax Yi，现在增加了图像生成器，就可以转变为计算Z*=argmax Yi 。
3. 将上面的图片生成器和分类器串在一起，就变成一个很深的神经网络。输入就是z，输出就是y。（分类器是之前已经训练好的）
4. 将找到的z*再带入到image generator，得到的图片就是我们想求的。（这就解释了机器认为cat长什么样）

通过图片生成器进行正则化，就得到机器所认为的图片的样子：

5. 用模型解释模型

其实另一种可能更泛化的解释 复杂模型 的方式，就是用一些操作，使用可解释的模型来解释复杂模型。我们一般用的可解释的模型是线性模型和比较简单的决策树模型。

5.1 用线性模型去解释

线性模型是最容易解释的模型，不论参数有多少个，每个参数的意义都是能很鲜明的说出这个对应项的情况的。那现在我们的目标是使用相同的输入，使线性模型和神经网络有相近的输出。

然而实际上并不能使用linear model来模拟整个neural network，线性模型过于简单，很多时候根本无法胜任这个任务，但可以用来模拟其中一个local region局部区域。

因此，LIME就应运而生：

5.2 Local Interpretable Model-Agnostic Explanations (LIME)

下图中input为x，output为y，都是一维的，表示Black Box中x和y的关系，由于我们并不能用linear model来模拟整个neural network，但可以用来模拟其中一个local region。

• step 1: 首先给出想要解释的point ，代入black box里面
• step 2 : 选取point x附近的点 （选取的点不同，得到的结果也不一样）
• step 3 : 用线性模型对选取的点进行拟合
• step 4 : 解释线性模型，也就解释了原来的NN 在这部分区域的行为

特别注意step 2 中nearby的选取， 当然，这个所谓的局部的大小，可能会对模型有极大的影响，因此调参也成为了一项技术活，使得达到更好的效果。

5.3 LIME对image的实际应用

解释下图中上部图片为什么会被认为是一只树蛙：

step 1 ：选择一个想要解释的数据点
step 2 ：选取附近样本：
将图像分割成一个个小块，作为单位进行分析，随机删除一些小块，构成不同的样本，然后输入到黑盒当中，得到识别出图片是树蛙的可能性。
step 3 ：用一个线性模型去拟合这个结果

如图，如果想用线性函数，我们需要对输入数据降维（先将图片特征提取成为m维向量），对于这个例子，我们可以用0-1变量表示某个小块是否存在。这样建立线性模型，就可以得到对应的每个区域的重要程度了。（M是指图片分割的块数）

step 4 ：解释学到的模型
如下图，我们现在则可以分析linear model这些参数：

• 如果权重Wm接近0，则说明这个区域与青蛙无关；
• 如果权重Wm为正数，则说明则说明这个区域与青蛙相关；
• 如果权重Wm为负数，则说明这个区域反而让机器认为它不是青蛙。

通过LIME，我们可以知道哪些图片的碎片对于识别结果是重要的，哪些是不重要的。

6. 用决策树去解释模型

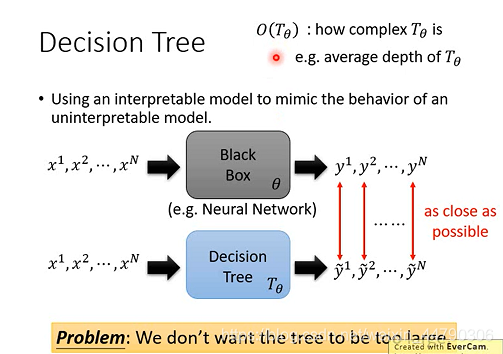
如果决策树足够复杂，那么理论上多复杂的神经网络都是可以被模拟的。我们要考虑两个方向：一个是决策树的契合程度，另一个是决策树的复杂程度（比如决策树的平均深度)。

但是我们希望决策树不能太复杂！

我们设neural network的参数为 θ，decision tree的参数为Tθ,使用O(Tθ)来表示Tθ的复杂度，复杂度可以用Tθ的树深度来表示，也可以用neural的个数来表示；现在我们的目标不仅是使两者输出相近，而且还需要使O(Tθ)的值最小化。

使O(Tθ)的值最小化的方法： 添加树正则项

训练一个特别的NN，在训练的时候就考虑到它要被决策树分析，所以在训练完后，就容易被决策树解释。

对原本的loss函数加上一个正则项 λO（Tθ），也就是在训练的时候就考虑了让决策树尽可能的小。但是值得注意的是这个正则项（正则化项是离散的）没法做偏导，所以没有办法做梯度计算。

解决办法：在一篇paper中，是另外用一个随机初始化的结构简单的NN，训练后可以模拟出决策树的参数。（输入是主神经网络z的参数，输出是z转成决策树之后的平均深度）将这个新训练的神经网络用在O（Tθ），这样整个式子就可以用梯度下降法。

7. 总结与展望

本章主要是围绕可解释性的机器学习展开，介绍了Explainable ML的基本方法和原理，可解释性的分类，原因，以及局部可解释性中的遮挡法与基于梯度与显著图的两种实现方法；与全局可解释性中用linear model和Decision Tree去解释复杂model的方法。但是如何限制决策树深度并且起到模拟作用的难题值得讨论的，其中对于决策树模型函数中树正则项无法直接进行梯度下降计算，应用训练神经网络去计算主神经网络转换成决策树的平均深度，这个做法对于NN有了更加进一步的理解，感觉到NN的强大与神奇之处。