一、学习主题
快速复习以下数学知识:
- 高等数学和线性代数
- 和概率论等知识;
- 完成阶段一作业
二、学习内容
高等数学
1.多元函数
(1)n维空间: 【元素+对应关系】
设
n
n
n 为取定的一个正整数,我们用
R
n
\mathbf{R}^{n}
Rn 表示
n
n
n 元有序实数组
(
x
1
,
x
2
,
?
?
,
\left(x_{1}, x_{2}, \cdots,\right.
(x1?,x2?,?,
x
n
)
\left.x_{n}\right)
xn?) 的全体所构成的集合, 即
R
n
=
R
×
R
×
?
×
R
=
{
(
x
1
,
x
2
,
?
?
,
x
n
)
∣
x
i
∈
R
,
i
=
1
,
2
,
?
?
,
n
}
\mathbf{R}^{n}=\mathbf{R} \times \mathbf{R} \times \cdots \times \mathbf{R}=\left\{\left(x_{1}, x_{2}, \cdots, x_{n}\right) \mid x_{i} \in \mathbf{R}, i=1,2, \cdots, n\right\}
Rn=R×R×?×R={(x1?,x2?,?,xn?)∣xi?∈R,i=1,2,?,n}
R
n
\mathbf{R}^{n}
Rn 中的元素
(
x
1
,
x
2
,
?
?
,
x
n
)
\left(x_{1}, x_{2}, \cdots, x_{n}\right)
(x1?,x2?,?,xn?) 有时也用单个字母
x
\boldsymbol{x}
x 来表示, 即
x
=
(
x
1
,
x
2
,
?
?
,
\boldsymbol{x}=\left(x_{1}, x_{2}, \cdots,\right.
x=(x1?,x2?,?,
x
n
)
.
\left.x_{n}\right) .
xn?). 当所有的
x
i
(
i
=
1
,
2
,
?
?
,
n
)
x_{i}(i=1,2, \cdots, n)
xi?(i=1,2,?,n) 都为零时,称这样的元素为
R
n
\mathbf{R}^{n}
Rn 中的零元,记为0或 O。
为了在集合
R
n
\mathbf{R}^{n}
Rn 中的元索之间建立联系,在
R
n
\mathbf{R}^{n}
Rn 中定义线代运算如下:
设
x
=
(
x
1
,
x
2
,
?
?
,
x
n
)
,
y
=
(
y
1
,
y
2
,
?
?
,
y
n
)
x=\left(x_{1}, x_{2}, \cdots, x_{n}\right), y=\left(y_{1}, y_{2}, \cdots, y_{n}\right)
x=(x1?,x2?,?,xn?),y=(y1?,y2?,?,yn?) 为
R
n
\mathbf{R}^{n}
Rn 中任意两个元素
,
λ
∈
R
, \lambda \in \mathbf{R}
,λ∈R规定:
x
+
y
=
(
x
1
+
y
1
,
x
2
+
y
2
,
?
?
,
x
n
+
y
n
)
,
λ
x
=
(
λ
x
1
,
λ
x
2
,
?
?
,
λ
x
n
)
\begin{array}{l} x+y=\left(x_{1}+y_{1}, x_{2}+y_{2}, \cdots, x_{n}+y_{n}\right), \\ \lambda x=\left(\lambda x_{1}, \lambda x_{2}, \cdots, \lambda x_{n}\right) \end{array}
x+y=(x1?+y1?,x2?+y2?,?,xn?+yn?),λx=(λx1?,λx2?,?,λxn?)?
这样定义了线性运算的集合
R
n
\mathbf{R}^{n}
Rn 称为
n
n
n 维空间.
R
n
\mathbf{R}^{n}
Rn 中点
x
=
(
x
1
,
x
2
,
?
?
,
x
n
)
\boldsymbol{x}=\left(x_{1}, x_{2}, \cdots, x_{n}\right)
x=(x1?,x2?,?,xn?) 和点
y
=
(
y
1
,
y
2
,
?
?
,
y
n
)
\boldsymbol{y}=\left(y_{1}, y_{2}, \cdots, y_{n}\right)
y=(y1?,y2?,?,yn?) 间的距离, 记作
ρ
(
x
,
y
)
,
\rho(x, y),
ρ(x,y), 规定
ρ
(
x
,
y
)
=
(
x
1
?
y
1
)
2
+
(
x
2
?
y
2
)
2
+
?
+
(
x
n
?
y
n
)
2
\rho(x, y)=\sqrt{\left(x_{1}-y_{1}\right)^{2}+\left(x_{2}-y_{2}\right)^{2}+\cdots+\left(x_{n}-y_{n}\right)^{2}}
ρ(x,y)=(x1??y1?)2+(x2??y2?)2+?+(xn??yn?)2?
(2)多元函数的偏导数
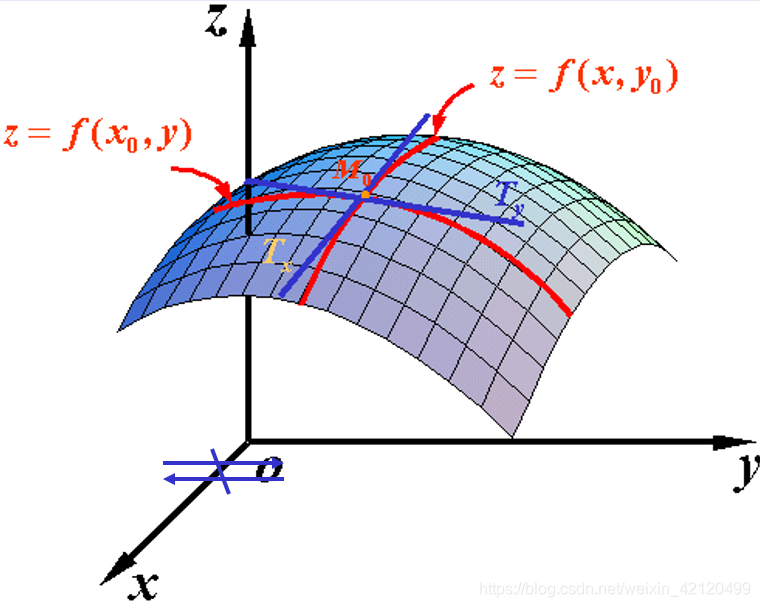
(3)梯度向量
梯度方向是函数增大最快的方向,负梯度方向是函数减小最快的方向。
梯度的本意是一个向量(矢量),表示某一函数在该点处的方向导数沿着该方向取得最大值,即函数在该点处沿着该方向(此梯度的方向)变化最快,变化率最大(为该梯度的模)。
定义:设二元函数
z
=
f
(
x
,
y
)
z=f(x, y)
z=f(x,y) 在平面区域D上具有一阶连续偏导数,则对于每一个点P(x, y)都可定出一个向量
{
?
f
?
x
,
?
f
?
y
}
=
f
x
(
x
,
y
)
i
ˉ
+
f
y
(
x
,
y
)
j
ˉ
,
\left\{\frac{\partial f}{\partial x}, \frac{\partial f}{\partial y}\right\}=f_{x}(x, y) \bar{i}+f_{y}(x, y) \bar{j},
{?x?f?,?y?f?}=fx?(x,y)iˉ+fy?(x,y)jˉ?, 该函数就称为函数
z
=
f
(
x
,
y
)
z=f(x, y)
z=f(x,y) 在点P
(
x
,
y
)
(\mathrm{x}, \mathrm{y})
(x,y) 的梯度,记作gradf
(
x
,
y
)
(\mathrm{x}, \mathrm{y})
(x,y) 或
?
f
(
x
,
y
)
\nabla f(x, y)
?f(x,y),即有:
gradf
?
(
x
,
y
)
=
?
f
(
x
,
y
)
=
{
?
f
?
x
,
?
f
?
y
}
=
f
x
(
x
,
y
)
i
ˉ
+
f
y
(
x
,
y
)
j
ˉ
\operatorname{gradf}(\mathrm{x}, \mathrm{y})=\nabla f(x, y)=\left\{\frac{\partial f}{\partial x}, \frac{\partial f}{\partial y}\right\}=f_{x}(x, y) \bar{i}+f_{y}(x, y) \bar{j}
gradf(x,y)=?f(x,y)={?x?f?,?y?f?}=fx?(x,y)iˉ+fy?(x,y)jˉ?
其中
?
=
?
?
x
i
ˉ
+
?
?
y
j
ˉ
\nabla=\frac{\partial}{\partial x} \bar{i}+\frac{\partial}{\partial y} \bar{j}
?=?x??iˉ+?y??jˉ? 称为(二维的)向量微分算子或Nabla算子,
?
f
=
?
f
?
x
i
ˉ
+
?
f
?
y
j
ˉ
\nabla f=\frac{\partial f}{\partial x} \bar{i}+\frac{\partial f}{\partial y} \bar{j}
?f=?x?f?iˉ+?y?f?jˉ? 。
(4)雅克比矩阵(Jacobian矩阵)
假设
F
:
R
n
→
R
m
F: \mathbb{R}_{n} \rightarrow \mathbb{R}_{m}
F:Rn?→Rm? 是一个从n维欧氏空间映射到到m维欧氏空间的函数。
这个函数由m个实函数组成:
y
1
(
x
1
,
?
?
,
x
n
)
,
?
?
,
y
m
(
x
1
,
?
?
,
x
n
)
y_{1}\left(x_{1}, \cdots, x_{n}\right), \cdots, y_{m}\left(x_{1}, \cdots, x_{n}\right)
y1?(x1?,?,xn?),?,ym?(x1?,?,xn?) 。这些函数的偏导数(如果存在)可以组成一个m行n列的矩阵,这个矩阵就是所谓的雅可 比矩阵:
[
?
y
1
?
x
1
?
?
y
1
?
x
n
?
?
?
?
y
m
?
x
1
?
?
y
m
?
x
n
]
\left[\begin{array}{ccc} \frac{\partial y_{1}}{\partial x_{1}} & \cdots & \frac{\partial y_{1}}{\partial x_{n}} \\ \vdots & \ddots & \vdots \\ \frac{\partial y_{m}}{\partial x_{1}} & \cdots & \frac{\partial y_{m}}{\partial x_{n}} \end{array}\right]
?????x1??y1????x1??ym????????xn??y1????xn??ym???????
(5)海森矩阵(Hessian matrix)
在数学中,海森矩阵(Hessian matrix 或 Hessian)是一个自变量为向量的实值函数的二阶偏导数组成的方块矩阵,假設有一实数函数
f
(
x
1
,
x
2
,
…
,
x
n
)
f\left(x_{1}, x_{2}, \ldots, x_{n}\right)
f(x1?,x2?,…,xn?)
如果
f
f
f 所有的二阶偏导数都存在,那么
f
f
f 的海森矩阵的第
i
j
i j
ij 项,即:
H
(
f
)
i
j
(
x
)
=
D
i
D
j
f
(
x
)
H(f)_{i j}(x)=D_{i} D_{j} f(x)
H(f)ij?(x)=Di?Dj?f(x)
其中
x
=
(
x
1
,
x
2
,
…
,
x
n
)
,
x=\left(x_{1}, x_{2}, \ldots, x_{n}\right),
x=(x1?,x2?,…,xn?), 即
H
(
f
)
=
[
?
2
f
?
x
1
2
?
2
f
?
x
1
?
x
2
?
?
2
f
?
x
1
?
x
n
?
2
f
?
x
2
?
x
1
?
2
f
?
x
2
2
?
?
2
f
?
x
2
?
x
n
?
?
?
?
?
2
f
?
x
n
?
x
1
?
2
f
?
x
n
?
x
2
?
?
2
f
?
x
n
2
]
H(f)=\left[\begin{array}{cccc} \frac{\partial^{2} f}{\partial x_{1}^{2}} & \frac{\partial^{2} f}{\partial x_{1} \partial x_{2}} & \cdots & \frac{\partial^{2} f}{\partial x_{1} \partial x_{n}} \\ \frac{\partial^{2} f}{\partial x_{2} \partial x_{1}} & \frac{\partial^{2} f}{\partial x_{2}^{2}} & \cdots & \frac{\partial^{2} f}{\partial x_{2} \partial x_{n}} \\ \vdots & \vdots & \ddots & \vdots \\ \frac{\partial^{2} f}{\partial x_{n} \partial x_{1}} & \frac{\partial^{2} f}{\partial x_{n} \partial x_{2}} & \cdots & \frac{\partial^{2} f}{\partial x_{n}^{2}} \end{array}\right]
H(f)=?????????x12??2f??x2??x1??2f???xn??x1??2f???x1??x2??2f??x22??2f???xn??x2??2f????????x1??xn??2f??x2??xn??2f???xn2??2f??????????
实际上,Hessian矩阵是梯度向量g(x)对自变量x的Jacobian矩阵。
2.函数极值
(1)最优性条件




线性代数
(1)向量空间
引出:线性方程组中n个m维向量的集合

(2)向量及其内积
【由二维空间引出】
向量内积(点积):结果是一个实数。
import numpy
#a=array([a1,a2,?,an])
#用代码表示两向量a?,b?的内积
c=dot(numpy.transpose(a),b)
#或
c=dot(a.T,b)
线性相关与线性无关:

向量的秩:极大线性无关组数量
Schmidt正交化:线性无关的向量->正交向量
(3)范数
向量映射为一个实数。向量的长度。

(4)矩阵
一个矩阵代表一个变换。
三、实验项目

(1)绘制3D图像
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
def plot3d(a,b):
x1 = np.linspace(-5, 5, 100)
x2 = np.linspace(-5, 5, 100)
x1, x2 = np.meshgrid(x1, x2)
y = (a - x1) ** 2 + b * (x2 - x1**2) ** 2
fig = plt.figure(figsize=(9,6))
ax = fig.gca(projection='3d')
surf = ax.plot_surface(x1, x2, y, rstride=2, cstride=2, cmap=plt.cm.coolwarm, linewidth=0.5, antialiased=True)
ax.set_xlabel('x1')
ax.set_ylabel('x2')
ax.set_zlabel('y')
for a in range(-2,3):
for b in range(-2,3):
plot3d(a,b)
plt.title("Rosenbrock(a = {},b = {})".format(a,b))
plt.show()
改变a,b取值观察可得,
b<0时,函数形状类似:

b=0时,函数形状:
a<0

a>0

b>0时,函数形状:

而a的取值对函数形状影响不大。
(2)求全局最小值
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
def func(x1,x2):
a = 1
b = 0
y = (a - x1) ** 2 + b * (x2 - x1**2) ** 2
return y
def Px1func(x1,x2): #x1偏导
return 2*(1-x1) - 2*(x2 - x1**2)*2*x1
def Px2func(x1,x2): #x2偏导
return 2*(x2 - x1**2)
def plot3d(a,b):
x1 = np.linspace(-3, 3, 50)
x2 = np.linspace(-3, 3, 50)
x1, x2 = np.meshgrid(x1, x2)
y = (a - x1) ** 2 + b * (x2 - x1**2) ** 2
fig = plt.figure(figsize=(9,6))
ax = fig.gca(projection='3d')
surf = ax.plot_surface(x1, x2, y, rstride=2, cstride=2, cmap=plt.cm.coolwarm, linewidth=0.5, antialiased=True)
ax.set_xlabel('x1')
ax.set_ylabel('x2')
ax.set_zlabel('y')
return ax
# 梯度下降法
step = 0.0001
#初始点
x10 = 2
x20 = 1
tag_x1 = [x10]
tag_x2 = [x20]
tag_y = [func(x10,x20)] #绘制点
new_x1 = x10
new_x2 = x20
flag = False
while not flag:
new_x1 -= step*Px1func(x10,x20)
new_x2 -= step*Px2func(x10,x20) #分别作梯度下降
if func(x10,x20) - func(new_x1,new_x2) < 1e-10: #精度
flag = True
x10 = new_x1
x20 = new_x2 #更新点
tag_x1.append(x10)
tag_x2.append(x20)
tag_y.append(func(x10,x20))
#绘制点/输出坐标
#初始
ax = plot3d(1,0)
ax.plot(tag_x1,tag_x2,tag_y,'r.')
plt.title('(x1,x2,y)~('+str(x10)+","+str(x20)+","+str(func(x10,x20))+')')
plt.show()
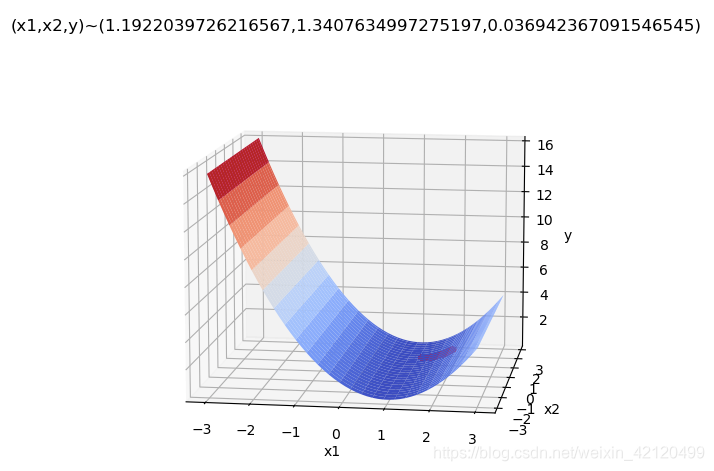

待修正:怎样得到全局最小?