[人工智能]GWAS分析中协变量的区分（性别？PCA？初生重？）

1. 电子书领取

前几天发了一篇GWAS电子书分享，异常火爆，阅读量8000+，很多人评价比较基础。这本电子书主要特点是比较基础，GLM模型用软件和R语言进行比较，如何添加数字协变量、因子协变量、PCA等内容，可以说是构建模型的基础。

今天，根据自己的理解，加上查阅的资料，介绍一下协变量的用法。

2. 什么是协变量

其实，GWAS中的协变量和一般模型中的协变量是不一样的。

一般模型：
$$y=F1+F2+x1+x2$$

• F1, F2为因子，特点是因子，比如不同颜色（红黄绿）
• x1，x2为协变量，特点是数值，不如初生重，PCA值等数值

协变量是指数字类型的变量。

GWAS模型中：
$$y=x1+x2$$

• GWAS中只有协变量，所谓的因子，也是协变量的一种
• 在GWAS分析汇总，因子也是转化为虚拟变量（dummy）放到模型中

实例演示

举个例子：

library(learnasreml)
data(fm)
head(fm)
str(fm)

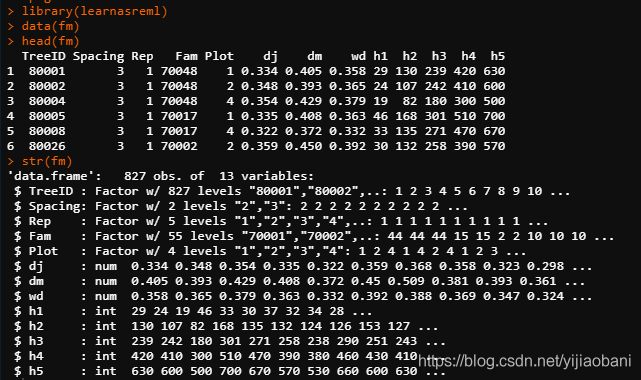
这个Rep有5个水平（5个重复），是因子类型。在方差分析中，它为因子：

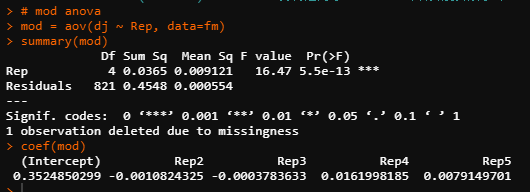
# mod anova
mod = aov(dj ~ Rep, data=fm)
summary(mod)
coef(mod)

这里面，Rep的方差分析，自由度为4，用coef查看系数时，给出每个水平的效应值。

在回归分析里面，它也为因子：

mod2 = lm(dj ~ Rep, data=fm)
summary(mod2)
anova(mod2)

在回归分析中，用的是lm函数，用summary给出每个水平的效应值，以及T检验的结果。用anova会打印出方差分析的结果。

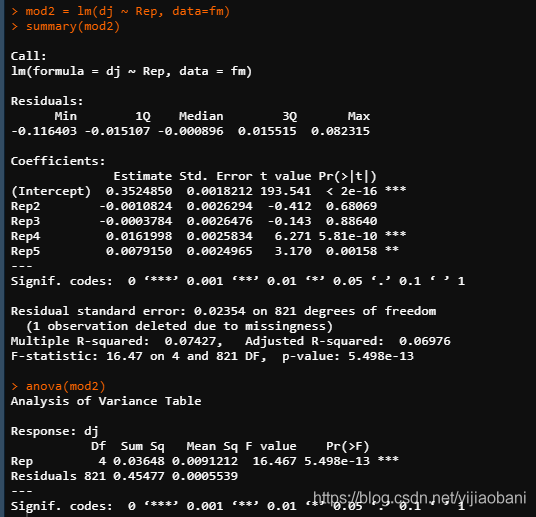
上面的例子可以看出aov和lm函数是等价的。

因子和协变量等价

如果我们将Rep变为虚拟变量，然后进行数字变量的回归分析，是什么样的？

library(useful)
xx = build.x(~Rep-1,data=fm,contrasts = F)
dat = cbind(xx[,-1],dj = fm$dj) %>% as.data.frame()
head(dat)
str(dat)

用R包useful的函数build.x将因子变为虚拟变量（数值变量），然后进行回归分析。

mod3 = lm(dj ~.,data=dat)
summary(mod3)

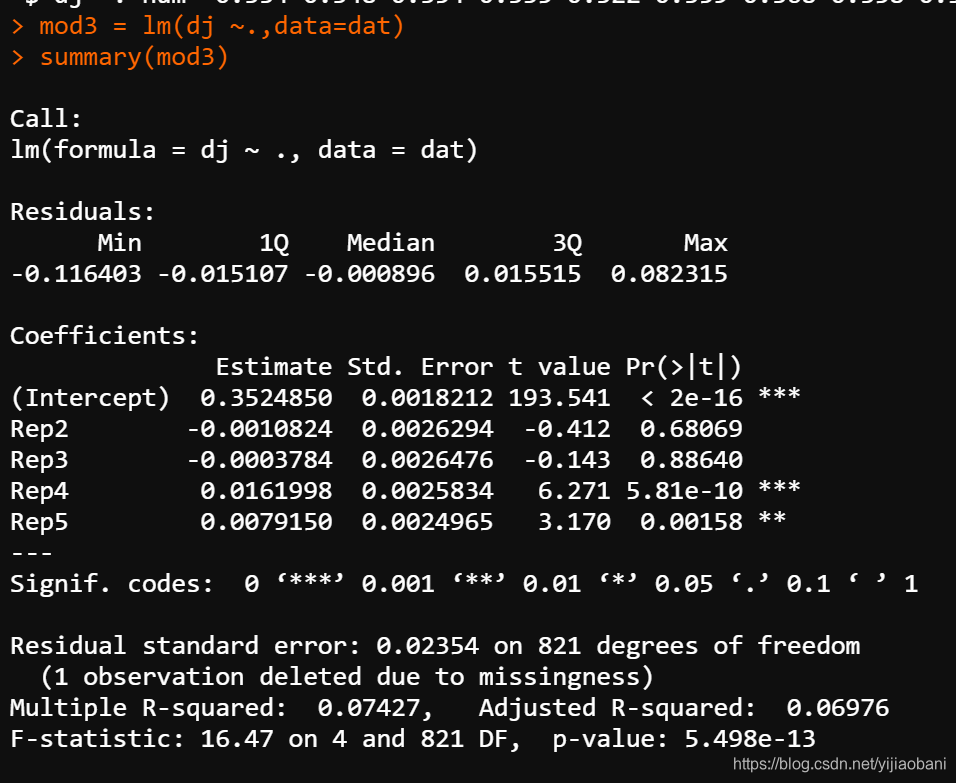
结果可以看出，用因子变为的虚拟变量（数字变量）结果是一样的。说明二者是等价的。

这也是说明了，在GWAS分析中，你以为因子和变量是两个类型，但是在GWAS模型中，他们最后都变为了协变量。

注意：

• R中因子第一个强制为0，所以这里在构建dummy变量时，第一列去掉
• R中默认是有截距（mu）的，所以再构建dummy变量时，将截距去掉

写道这里，我想到了一句话：

当你将方差分析和回归分析看做是一样的东西时，你就进阶了。

所以，我进阶了，哈哈。

所以，统计课本里面，方差分析和线性回归分析，都是基于一般线性模型（GLM），放到GWAS分析中，就可以解释因子协变量和数字协变量，以及PCA协变量的区别了。

无它，在GWAS模型中，都会变为数值协变量。

下一次推文，讲解如何在plink中构建协变量，以及如何在R语言中构建协变量。欢迎继续关注。