Datawhale组队学习第27期:集成学习
本次学习的指导老师萌弟的教学视频
本贴为学习记录帖,有任何问题欢迎随时交流~
部分内容可能还不完整,后期随着知识积累逐步完善。
开始时间:2021年7月13日
最新更新:2021年7月13日(Task1数学基础)
文章目录
【Task01】数学基础
一、高等数学
1. 多元函数
-
n维空间
- 元素:由n元有序实数组的全体构成的集合
- 运算:和运算与数乘运算(线性运算,封闭性)
-
距离(这里指的是欧氏距离,可以联系后面的范数)
ρ ( x , y ) = ( x 1 ? y 1 ) 2 + ( x 2 ? y 2 ) 2 + ? + ( x n ? y n ) 2 \rho(x, y)=\sqrt{\left(x_{1}-y_{1}\right)^{2}+\left(x_{2}-y_{2}\right)^{2}+\cdots+\left(x_{n}-y_{n}\right)^{2}} ρ(x,y)=(x1??y1?)2+(x2??y2?)2+?+(xn??yn?)2?- 更一般的距离定义(LP距离,p=2时就是欧氏距离):
L p ( x i , x j ) = ( ∑ l = 1 n ∣ x i ( l ) ? x j ( l ) ∣ p ) 1 p L_{p}\left(x_{i}, x_{j}\right)=\left(\sum_{l=1}^{n}\left|x_{i}^{(l)}-x_{j}^{(l)}\right|^{p}\right)^{\frac{1}{p}} Lp?(xi?,xj?)=(l=1∑n?∣∣∣?xi(l)??xj(l)?∣∣∣?p)p1?
- 更一般的距离定义(LP距离,p=2时就是欧氏距离):
-
二元函数
- 定义域是一个平面
- 二元函数是一个曲顶柱体
2. 雅可比矩阵和黑塞矩阵
-
梯度向量
- 某一函数在该点处的方向导数沿着方向取得的最大值
- 方向、变化率(模)
- 一般这里默认是增大最快的方向(正常来说有增大或减小)
- 负梯度是指减少最快的方向
-
J a c o b i a n Jacobian Jacobian矩阵
-
设存在一个函数,使得n维空间映射到m维空间
-
函数由m个实函数组成,n个变量
-
所有的实函数的偏导数组成m行n列的矩阵,即雅可比矩阵
-
每行都是对应函数的梯度
-
-
H e s s i a n Hessian Hessian矩阵
- 类似于雅可比矩阵,但存储的是二阶导数
H ( f ) = [ ? 2 f ? x i ? x j ] n × n H(f) = [\frac{\partial^2f}{\partial x_i \partial x_j}]_{n \times n} H(f)=[?xi??xj??2f?]n×n?
- Hessian矩阵是梯度向量 g ( x ) g(x) g(x)对自变量 x x x的 J a c o b i a n Jacobian Jacobian矩阵。
3. 极值
极值:设函数
f
(
x
)
f(x)
f(x) 在点
x
0
x_{0}
x0? 的某邻域
U
(
x
0
)
U\left(x_{0}\right)
U(x0?) 内有定义,如果对于去心邻域U
(
x
0
)
\left(x_{0}\right)
(x0?) 内的任一
x
x
x, 有 A:
f
(
x
)
<
f
(
x
0
)
?或?
f
(
x
)
>
f
(
x
0
)
f(x)<f\left(x_{0}\right) \text { 或 } f(x)>f\left(x_{0}\right)
f(x)<f(x0?)?或?f(x)>f(x0?)
-
鞍点是比较适合用于对抗
-
极值局部概念,最值是全局概念
-
最优性条件
- 一元函数情况
- 一阶导数充分条件
- 二阶导数充分条件
-
多元函数情况下
设n多元实函数 f ( x 1 , x 2 , ? ? , x n ) f\left(x_{1}, x_{2}, \cdots, x_{n}\right) f(x1?,x2?,?,xn?) 在点 M 0 ( a 1 , a 2 , … , a n ) M_{0}\left(a_{1}, a_{2}, \ldots, a_{n}\right) M0?(a1?,a2?,…,an?) 的邻域内有二阶连续偏导,若有:
? f ? x j ∣ ( a 1 , a 2 , … , a n ) = 0 , j = 1 , 2 , … , n \left.\frac{\partial f}{\partial x_{j}}\right|_{\left(a_{1}, a_{2}, \ldots, a_{n}\right)}=0, j=1,2, \ldots, n ?xj??f?∣∣∣∣?(a1?,a2?,…,an?)?=0,j=1,2,…,n
H ( f ) = [ ? 2 f ? x 1 2 ? 2 f ? x 1 ? x 2 ? ? 2 f ? x 1 ? x n ? 2 f ? x 2 ? x 1 ? 2 f ? x 2 2 ? ? 2 f ? x 2 ? x n ? ? ? ? ? 2 f ? x n ? x 1 ? 2 f ? x n ? x 2 ? ? 2 f ? x n 2 ] H(f)=\left[\begin{array}{cccc} \frac{\partial^{2} f}{\partial x_{1}^{2}} & \frac{\partial^{2} f}{\partial x_{1} \partial x_{2}} & \cdots & \frac{\partial^{2} f}{\partial x_{1} \partial x_{n}} \\ \frac{\partial^{2} f}{\partial x_{2} \partial x_{1}} & \frac{\partial^{2} f}{\partial x_{2}^{2}} & \cdots & \frac{\partial^{2} f}{\partial x_{2} \partial x_{n}} \\ \vdots & \vdots & \ddots & \vdots \\ \frac{\partial^{2} f}{\partial x_{n} \partial x_{1}} & \frac{\partial^{2} f}{\partial x_{n} \partial x_{2}} & \cdots & \frac{\partial^{2} f}{\partial x_{n}^{2}} \end{array}\right] H(f)=?????????x12??2f??x2??x1??2f???xn??x1??2f???x1??x2??2f??x22??2f???xn??x2??2f????????x1??xn??2f??x2??xn??2f???xn2??2f??????????
? (1) 当 H ( f ) H(f) H(f)正定矩阵时, f ( x 1 , x 2 , ? ? , x n ) f\left(x_{1}, x_{2}, \cdots, x_{n}\right) f(x1?,x2?,?,xn?) 在 M 0 ( a 1 , a 2 , … , a n ) M_{0}\left(a_{1}, a_{2}, \ldots, a_{n}\right) M0?(a1?,a2?,…,an?) 处是极小值;
? (2) 当 H ( f ) H(f) H(f)负定矩阵时, f ( x 1 , x 2 , ? ? , x n ) f\left(x_{1}, x_{2}, \cdots, x_{n}\right) f(x1?,x2?,?,xn?) 在 M 0 ( a 1 , a 2 , … , a n ) M_{0}\left(a_{1}, a_{2}, \ldots, a_{n}\right) M0?(a1?,a2?,…,an?) 处是极大值;
? (3) 当 H ( f ) H(f) H(f)不定矩阵时, M 0 ( a 1 , a 2 , … , a n ) M_{0}\left(a_{1}, a_{2}, \ldots, a_{n}\right) M0?(a1?,a2?,…,an?) 不是极值点。
? (4) 当A为半正定矩阵或半负定矩阵时, M 0 ( a 1 , a 2 , … , a n ) M_{0}\left(a_{1}, a_{2}, \ldots, a_{n}\right) M0?(a1?,a2?,…,an?) 是“可疑"极值点,尚需要利用其他方法来判定。
二、线性代数
-
向量空间
-
内积/点积
import numpy as np a = np.array([a1, a2, ..., an]) c = np.dot(np.transpose(a), b) # 内积 c = np.dot(a.T, b) -
线性相关与线性无关
- 二维中线性相关即平行,线性无关是不平行
- 以二维向量空间为例,若存在两个不平行(线性无关)的向量,该空间的所有向量都可以由这两个向量线性表示。
- 该向量空间的线性无关向量组称为该向量空间的基。
- 极大线性无关组代表某个方程的信息\解,个数又称为秩。
-
施密特正交化
- 正交,内积为0
- 单位化,模长为1
from sympy.matrices import Matrix, GramSchmidit -
范数
-
长度(从二维推广出来的)
-
由向量映射到常数
-
性质
- 正定性
- 齐次性
- 三角不等式
-
-
矩阵
- 本质上是一个变换
- 行列式
- 矩阵变换的程度、幅度(二维中表示变化面积)
numpy.linalg.det()可以计算行列式
-
矩阵范数
- 使用
np.linalg.norm(x, ord=)
- 使用
-
特征值和特征向量
np.linaleig(x)
-
迹
- 变换幅度的速率
-
正定矩阵
- 所有矩阵的特征值都是正的
三、概率论基础
1. 基本的概念
-
随机试验
-
可重复性
-
可观察性
-
不确定性
-
-
样本空间
- 全部样本点的集合
-
概率
- 多次重复实验中,事件A发生的频率稳定在常数p附近
-
条件概率、独立性
-
全概率公式和贝叶斯公式
2. 随机变量
-
定义:
随机变量 X X X是定义在样本空间 Ω \Omega Ω上的函数,当 x x x是 X X X的观测值时,存在 Ω \Omega Ω中的 w w w使得 x = X ( w ) x = X(w) x=X(w)
- 本质上是一个函数
- 随机现象映射到实数域上
- 离散随机变量、连续随机变量
-
概率密度与分布列
- 离散型的概率分布
- 二项分布
- 伯努利分布
- 泊松分布
- 连续性的概率分布
- 均匀分布
- 正态分布
- 离散型的概率分布
-
特征数
- 期望
- 方差(标准差)
3. 随机向量
-
定义:
随机向量 ( X 1 , X 2 , . . . , X n ) (X_1, X_2, ..., X_n) (X1?,X2?,...,Xn?)是定义在样本空间 Ω \Omega Ω的n元函数(即由有限个随机变量组成的向量),当 ( x 1 , x 2 , . . . , x n ) (x_1, x_2,...,x_n) (x1?,x2?,...,xn?)是 ( X 1 , X 2 , . . . , X n ) (X_1, X_2, ..., X_n) (X1?,X2?,...,Xn?)的观测值时,存在 w w w使得 ( x 1 , x 2 , . . . , x n ) = ( X 1 ( w ) , X 2 ( w ) , . . . , X n ( w ) ) (x_1, x_2,...,x_n) = (X_1(w), X_2(w), ..., X_n(w)) (x1?,x2?,...,xn?)=(X1?(w),X2?(w),...,Xn?(w)) ,这时称 ( x 1 , x 2 , . . . , x n ) (x_1, x_2,...,x_n) (x1?,x2?,...,xn?)为 ( X 1 , X 2 , . . . , X n ) (X_1, X_2, ..., X_n) (X1?,X2?,...,Xn?)的一次观测或一次实现。
-
联合概率密度与分布列
- 边际分布
- 条件概率分布
-
特征数
- 期望
- 方差
- 协方差:如果两个随机向量的协方差阵是对角阵,则随机向量是无关的
-
无限个随机变量
- 大数定律
- 独立同分布,随样本量增大,样本均值收敛到总体均值
- 中心极限定理
- 样本量足够大,样本均值的分布服从正态分布
- 大数定律
四、数理统计
1. 主要分支:
- 参数估计(重点)
- 假设检验
2. 总体与样本
- 关键前提:随机抽样
- 样本与总体是同分布的
- 不同样本之间是独立的
- 格里纹科定理
- 经验分布函数
- 当样本n趋向于无穷时,经验分布函数依概率收敛于总体分布函数
- 参数
- 总体中确定但未知的常量(这是频率学派)
- 参数是随机变量(贝叶斯学派)
3. 极大似然估计MLE(频率学派)
θ ? = a r g m a x P ( X ∣ θ ) \theta^* = argmaxP(X|\theta) θ?=argmaxP(X∣θ)
- 哪一个参数最有可能让分布产生给定的样本
- 观察样本的联合概率(引入独立性,变成连乘)
- 目标函数:找到一组参数,使得联合概率达到最大
- 处理:对联合概率取对数,不改变性质
- 求解算法:
- 数值求解,直接求偏导
- 梯度下降法
- 牛顿法
4. 贝叶斯估计(贝叶斯学派)
-
小数据问题,容易出现过拟合
- 贝叶斯模型(无穷个模型)与集成学习(有限个模型)
- 在模型中融入不确定性,利用前人的经验
- 对模型进行压缩
-
最大后验估计MAP
θ ? = a r g m a x P ( θ ∣ X ) = a r g m a x P ( X , θ ) P ( X ) = a r g m a x P ( X ∣ θ ) ? P ( θ ) P ( X ) = a r g m a x P ( X ∣ θ ) ? P ( θ ) \theta^* = argmax P(\theta|X) = argmax\frac{P(X,\theta)}{P(X)} = argmax\frac{P(X|\theta) \cdot P(\theta)}{P(X)} = argmaxP(X|\theta) \cdot P(\theta) θ?=argmaxP(θ∣X)=argmaxP(X)P(X,θ)?=argmaxP(X)P(X∣θ)?P(θ)?=argmaxP(X∣θ)?P(θ)-
可以看作对极大似然进行了归一化
-
最优化问题等价于后验概率最大
-
P ( X ) P(X) P(X) 比较难算,一般是采用近似推断,对参数后验分布进行采样,取得其均值近似。
P ( X ) = ∫ θ P ( X , θ ) d θ = ∫ θ P ( y ′ ∣ x ′ ; θ ) ? f ( θ ) d θ = 1 S ∑ i = 1 S P ( y ′ ∣ x ′ ; θ S ) 其 中 , θ S ~ P ( θ ∣ X ) P(X) = \int_{\theta} P(X,\theta) d\theta = \int_{\theta}P(y'|x'; \theta) \cdot f(\theta)d\theta = \frac{1}{S}\sum\limits_{i=1}^{S}P(y'|x'; \theta^S) \\ 其中,\theta^S \sim P(\theta|X) P(X)=∫θ?P(X,θ)dθ=∫θ?P(y′∣x′;θ)?f(θ)dθ=S1?i=1∑S?P(y′∣x′;θS)其中,θS~P(θ∣X)
-
-
预测比较难,算法性能目前较低
五、随机过程
1. 随机过程
-
定义:引入了时间变量T(不是随机的),设T为 ( ? ∞ , + ∞ ) (-\infty,+\infty) (?∞,+∞)的子集,若对每个 t ∈ T t\in T t∈T, X t X_t Xt?是随机变量,则称随机变量的集合 { X t ∣ t ∈ T } \{X_t|t\in T \} {Xt?∣t∈T}是随机过程。当每个t都有一次观测,那么会形成一条曲线,则称这条曲线为一条轨道或一条轨迹。
? 例如:某一商店一天的顾客数。
-
有限维分布
? 对于任何正整数m和T中互不相同的 t 1 , . . . , t m t_1,...,t_m t1?,...,tm?,称 ( X t 1 , . . . , X t m ) (X_{t1},...,X_{tm}) (Xt1?,...,Xtm?)的联合分布为随机过程 { X t ∣ t ∈ T } \{X_t|t \in T\} {Xt?∣t∈T} 的一个有限维分布,称全体的有限维分布为该随机过程的概率分布。
-
随机过程同分布
如果两个随机过程有相同的有限维分布,称它们为同分布。
-
随机过程独立性
? 如果一随机过程中任意选取的 { X t 1 , . . . , X t i } \{ X_{t1}, ..., X_{ti} \} {Xt1?,...,Xti?}与另一随机过程中任意选出的 { Y t 1 , . . . , Y t i } \{ Y_{t1}, ..., Y_{ti} \} {Yt1?,...,Yti?}是相互独立的,则称它们的两个随机过程独立。
2. 随机序列
-
定义:如果时间集合T是整数,就是一个随机序列(时间序列),记作 X n X_n Xn?。
-
独立增量性
? 互不相交的时间段内发生事件的个数是相互独立,对于任意正整数n和$0 \le t_1 \le t_2 \le … \le t_n , 随 机 变 量 ,随机变量 ,随机变量N(0),N(0,t_1),N(t_1,t_2),…,N(t_{n-1}, t_n)$是相互独立
-
平稳增量性
? 长度相等的时间段内,事件发生的个数的概率分布是相同的,对于任意 s > 0 , t 2 > t 1 ≥ 0 s > 0, t_2 >t_1 \ge 0 s>0,t2?>t1?≥0,随机变量 N ( t 1 + s , t 2 + s ) 与 N ( t 1 , t 2 ) N(t_1 + s, t_2 + s)与N(t_1, t_2) N(t1?+s,t2?+s)与N(t1?,t2?)同分布。
-
严平稳和宽平稳
- 严平稳:相同时间段内,联合概率分布相同
- 宽平稳:均值是常数,协方差只与时间差有关
-
独立增量过程
- 任意时刻的增量是相互独立。
-
平稳增量过程
- 一定时间差下的增量相同。
-
平稳独立增量过程
- 兼有独立增量和平稳增量
2. 计数过程
- 随机过程
{
N
(
t
)
,
t
≥
0
}
\{N(t), t \ge 0\}
{N(t),t≥0}为计数过程 ,
N
(
t
)
N(t)
N(t) 表示从 0 到 t 时 刻某一特定事件A发生的次数
- N ( t ) ≥ 0 N(t) \ge 0 N(t)≥0且取值为整数
- 当 s < t s < t s<t 时, N ( s ) ≤ N ( t ) N(s) \le N(t) N(s)≤N(t)且 N ( s ) ? N ( t ) N(s) - N(t) N(s)?N(t)表示 ( s , t ] (s, t] (s,t]时间内事件A发生的次数。
3. 泊松过程
-
计数过程 { N ( t ) , t ≥ 0 } \{N(t), t \ge 0\} {N(t),t≥0}称为参数为 λ ( λ > 0 ) \lambda(\lambda > 0) λ(λ>0)的Poisson过程,有:
-
N ( 0 ) = 0 N(0) = 0 N(0)=0
-
过程有独立增量
-
任一长度为 t t t 的时间区间中事件发生的次数均服从均值为 λ t \lambda t λt的Poisson分布
对 一 切 s ≥ 0 , t > 0 , 有 : P { N ( t + s ) ? N ( s ) = n } = e ? λ t ( λ t ) n n ! , n = 0 , 1 , 2 , . . . 对一切s\ge 0, t >0, 有:\\ P\{N(t+s) - N(s) = n \} = e^{-\lambda t} \frac{(\lambda t)^n}{n!}, n=0,1,2,... 对一切s≥0,t>0,有:P{N(t+s)?N(s)=n}=e?λtn!(λt)n?,n=0,1,2,...
-
-
{ N ( t + s ) ? N ( s ) = n } \{N(t+s) - N(s) = n \} {N(t+s)?N(s)=n}与起始点s无关,只与时间间隔t有关,具有平稳增量性。
-
设 { N ( t ) } \{ N(t) \} {N(t)}是强度为 λ \lambda λ的泊松过程,容易计算 E ( N ( t ) ) = λ t E(N(t)) = \lambda t E(N(t))=λt,而 λ = E ( N ( t ) ) t \lambda = \frac{E(N(t))}{t} λ=tE(N(t))?是单位时间内事件发生的次数的平均数。
-
伯努利试验中每次实验成功的概率很小,随试验增多,二项分布会逼近Poisson分布
-
设 λ > 0 \lambda > 0 λ>0是一个常数,计数过程 { N ( t ) } \{ N(t) \} {N(t)}为满足强度为 λ \lambda λ的泊松过程的条件:
- N ( 0 ) = 0 N(0)= 0 N(0)=0
- { N ( t ) } \{N(t)\} {N(t)} 是独立增量过程,具有平稳增量性
- 一般性:对任何 t ≥ 0 t\ge 0 t≥0,当发生的次数 h h h趋向于0时,有: P ( N ( h ) = 1 ) = λ h + o ( h ) P(N(h)=1)=\lambda h + o(h) P(N(h)=1)=λh+o(h)与 P ( N ( h ) ≥ 2 ) = o ( h ) P(N(h) \ge 2)=o(h) P(N(h)≥2)=o(h)
4. 呼叫泊松流
-
呼叫流
设 N ( t ) {N(t)} N(t)是强度为 λ \lambda λ的泊松过程,定义 S 0 = 0 S_0=0 S0?=0,用 S n S_n Sn?表示第n个事件发生的时刻,又称第n个到达时刻或第n个呼叫时,由于 S 0 , S 1 , . . . , S n S_0,S_1,...,S_n S0?,S1?,...,Sn?依次到达, { S t } \{S_t\} {St?}为泊松过程 { N ( t ) } \{N(t)\} {N(t)}的呼叫流。(转换思想,区别于完备事件)
-
基本关系:
{ N ( t ) ≥ n } = { S n ≤ t } { N ( t ) = n } = { S n ≤ t < S n + 1 } \{ N(t) \ge n \} = \{ S_n \le t \} \\ \{ N(t) = n \} = \{ S_n \le t < S_{n+1} \} {N(t)≥n}={Sn?≤t}{N(t)=n}={Sn?≤t<Sn+1?} -
等待间隔: X n = S n ? S n ? 1 X_n = S_n - S_{n-1} Xn?=Sn??Sn?1?
-
泊松过程 { N ( t ) } \{N(t) \} {N(t)}的等待间隔 X 1 , X 2 , . . . , X n , . . . X_1, X_2,...,X_n,... X1?,X2?,...,Xn?,...是来自指数总体 ? ( λ ) \epsilon(\lambda) ?(λ)的随机变量。
-
泊松过程的汇合与分流
-
对于强度为 λ 1 \lambda_1 λ1?的泊松过程 { N 1 ( t ) } \{N_1(t)\} {N1?(t)}和强度为 λ 2 \lambda_2 λ2?的泊松过程 { N 2 ( t ) } \{N_2(t)\} {N2?(t)},两者独立且有
N ( t ) = N 1 ( t ) + N 2 ( t ) N(t) = N_1(t) + N_2(t) N(t)=N1?(t)+N2?(t) -
两个独立的泊松过程之和也是泊松过程,强度 λ = λ 1 + λ 2 \lambda = \lambda_1 + \lambda_2 λ=λ1?+λ2?。
-
从另一个角度看,如将强度按 p : 1 ? p p:1-p p:1?p进行分流的话,两个分流依旧是泊松过程,具体可以参考这篇文章。
-
5.马尔可夫随机过程
-
马尔可夫链:未来只与现在有关,与过去无关(独立)
-
随机过程 { X n , n = 0 , 1 , 2 , . . . } \{ X_n, n=0,1,2,... \} {Xn?,n=0,1,2,...}称为Markov链,若它只取有限或可列个值,并且对任意的 n ≥ 0 n \ge 0 n≥0及任意状态 i , j , i 0 , i 1 , . . . , i n ? 1 i,j,i_0,i_1,..., i_{n-1} i,j,i0?,i1?,...,in?1?有如下结果:
P ( X n + 1 = k n + 1 ∣ X n = k n , X n ? 1 = k n ? 1 , . . . , X 0 = k 0 ) = P ( X n + 1 = k n + 1 ∣ X n = k n ) P(X_{n+1} = k_{n+1} | X_n = k_n, X_{n-1} =k_{n-1},...,X_0=k_0) = P(X_{n+1} = k_{n+1} | X_n = k_n) P(Xn+1?=kn+1?∣Xn?=kn?,Xn?1?=kn?1?,...,X0?=k0?)=P(Xn+1?=kn+1?∣Xn?=kn?)
X n = i X_n=i Xn?=i表示过程时刻n处于状态 i i i,称 0 , 1 , 2 , . . . {0,1,2,...} 0,1,2,...为该过程的状态空间,记为 S S S。
-
(一步)转移概率:
{ X n , n = 0 , 1 , 2 , . . . } \{X_n, n=0,1,2,...\} {Xn?,n=0,1,2,...}的一步转移概率,记为 p i j p_{ij} pij?,表示状态 i i i的过程下一步转移到状态 j j j的概率
-
(一步)概率转移矩阵: P = ( p i j ) = ( p i j ) i , j ∈ I P = (p_{ij}) = (p_{ij})_{i,j \in I} P=(pij?)=(pij?)i,j∈I?
6. 鞅
-
? 设 { Y n , n ≥ 0 } \{Y_n, n \ge 0\} {Yn?,n≥0}为一随机变量序列。若对于随机 ? n > 0 \forall n > 0 ?n>0,有随机过程 { X n , n ≥ 0 } \{X_n, n \ge 0\} {Xn?,n≥0},其中 X n X_n Xn?是 ( Y 0 , Y 1 , . . . , Y n ) (Y_0, Y_1,...,Y_n) (Y0?,Y1?,...,Yn?)的函数,$E(|X_n|) < \infty 且 且 且E(X_{n+1}|Y_0, …, Y_n) = X_n , 则 称 随 机 过 程 ,则称随机过程 ,则称随机过程{X_n, n \ge 0} 是 关 于 是关于 是关于{Y_n, n \ge 0}$的鞅。
-
常用于定价公平性和系统稳定性研究中。
-
高斯过程
-
无限维度的高斯分布(这里无限维度指的是无限多个高斯随机变量)
-
定义:
一随机过程 X = { X t } t ∈ T X=\{X_t \}_{t \in T} X={Xt?}t∈T?,对于一个连续域 T T T,若从连续域上任选 n n n个时刻,即: ? t 1 , t 2 , . . . , t n ∈ T \forall t_1,t_2,...,t_n \in T ?t1?,t2?,...,tn?∈T,获得的 n n n维向量 { ξ 1 , ξ 2 , . . . , ξ n } \{\xi_1, \xi_2,...,\xi_n \} {ξ1?,ξ2?,...,ξn?}都是高斯随机向量,则称 { X t } \{X_t\} {Xt?}为高斯过程。
-
六、课后作业(Rosenbrock函数)
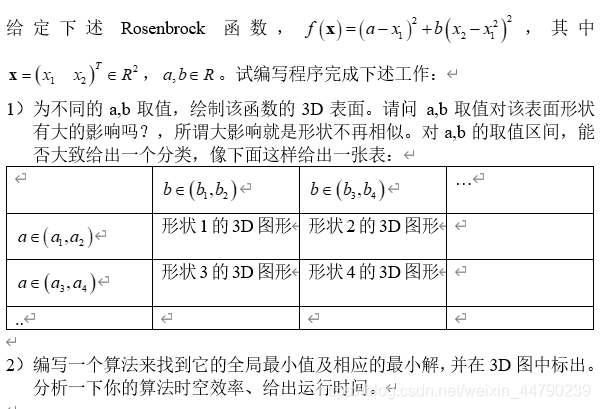
目前只做了第1题:
1.图像(基于Python)
import numpy as np
import matplotlib.pyplot as plt
from ipywidgets import *
@interact(a=(-5, 5, 0.1), b=(-10, 10, 1), h=(-360,360,30), w=(-360,360,30))
def plot_3d(a=0, b=10, h=20, w=150):
plt.figure(figsize=(10, 10))
x = np.linspace(-1.5, 1.5, 300)
y = np.linspace(-1.5, 1.5, 300)
X, Y = np.meshgrid(x, y)
Z = (a - X) ** 2 + b * (Y - X ** 2) ** 2
ax = plt.subplot(1, 1, 1, projection='3d')
ax.plot_surface(X, Y, Z, cmap='plasma')
ax.set_xlabel('x')
ax.set_ylabel('y')
ax.set_zlabel('z')
ax.view_init(elev=h, azim=w)
plt.title('Rosenbrock')
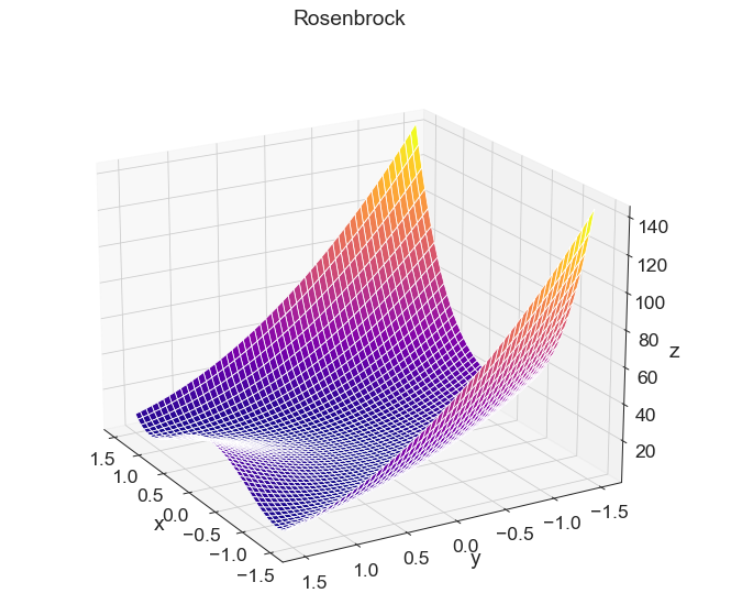
- 当b大于0时,图像如下:
- 当b小于0时,图像如下:

- 当b=0时,图像如下:
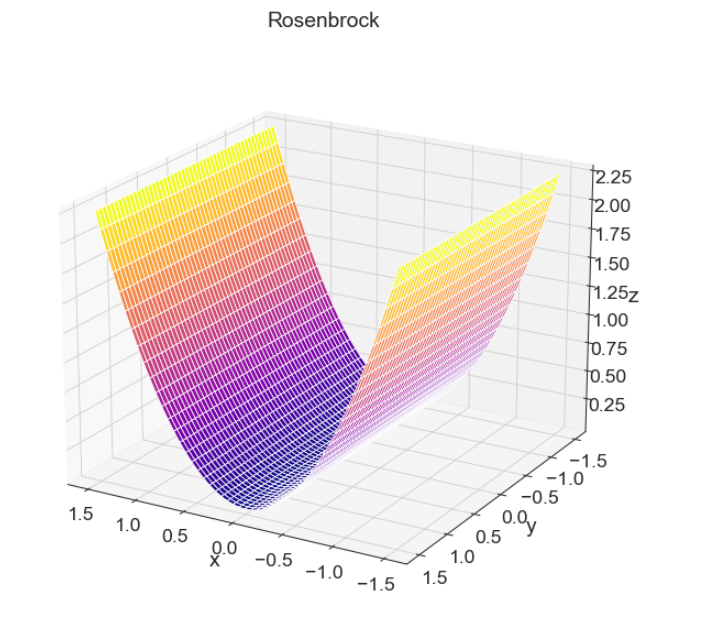
- 当b不变,a变动时,体现的是下凸曲面的变动。
- 在b为0时,体现的是曲面沿着x轴平移。
- 在b不为0时,曲面两边发生摆动。
2.关于最小值的思考
- 本题没有来得及做出来,但如果从直观上来看,当b=0时比较容易取得最小值。其他情况需要考虑最优化的算法。