
雅可比矩阵
-
定义:

-
几何意义:该函数变化率最大的方向
当该函数为二次函数时,其雅可比矩阵即为梯度向量。
极值与二次型
由二次型的知识可知:一个线性方程组可以写成如下形式
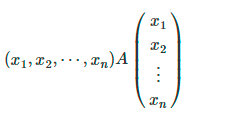 ,
,
故该线性方程组的图像由矩阵A决定,以二次多项式为例:当矩阵A正定时,图像开口向上,故有极小值;当A负定时,图像开口向下,故有极大值。
黑塞矩阵为正定矩阵,在该点取极小值
黑塞矩阵为负定矩阵,在该点取极大值
黑塞矩阵为不定矩阵,在该点不是极值点
黑塞矩阵为半正(负)定矩阵,不一定是极值点
最大线性无关组与矩阵的秩
最大线性无关组定义:设S是一个n维向量组,α1,α2,…αr 是S的一个部分组,如果(1) α1,α2,…αr 线性无关;(2) 向量组S中每一个向量均可由此部分组线性表示,那么α1,α2,…αr 称为向量组S的一个极大线性无关组,或极大无关组。
矩阵秩的定义:
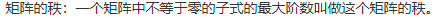
二者关系:在一个矩阵中,该矩阵的秩与最大线性无关组中的元素个数相等
极大似然估计
极大似然估计是估计总体参数的一种方法。根据密度函数构造似然函数,再对似然函数取对数,使其形式简化,然后求该对数函数关于总体参数的导数。当似然函数取极大值,即导函数为0时,此时的估计值为参数的极大似然估计
贝叶斯估计
以估计总体均值为例。赋予参数空间中每一个参数相应的权重,计算该参数空间中参数的加权平均值,以此来估计总体均值(可以考虑到不定因素)
作业
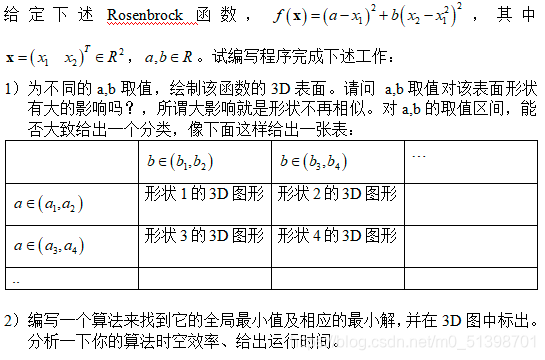
(1)
#导入数据包
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
#定义函数
def f(a,b,x_1,x_2):
return (a-x_1)**2+b*(x_2-x_1**2)**2
#绘制三维图像
from mpl_toolkits.mplot3d import Axes3D
plt.figure(figsize=(8,8))
ax3 = plt.axes(projection='3d')
x_1=np.linspace(-10,10,5000)
x_2=np.linspace(-10,10,5000)
X_1, X_2 = np.meshgrid(x_1, x_2)
a=0
b=0
z=f(a,b,X_1,X_2)
ax3.plot_surface(X_1,X_2,z,cmap='rainbow')
plt.show()
所的图像如下:
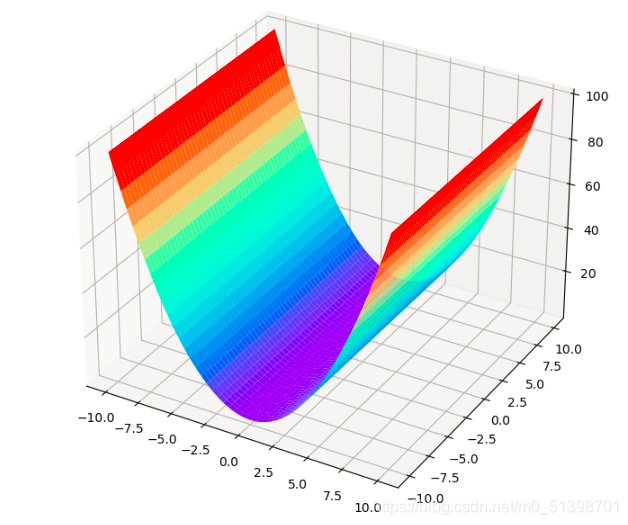
通过改变a,b的值发现,当a的值不断增大,b保持不变时,图像会逐渐向右平移,以a=3,b=0为例:
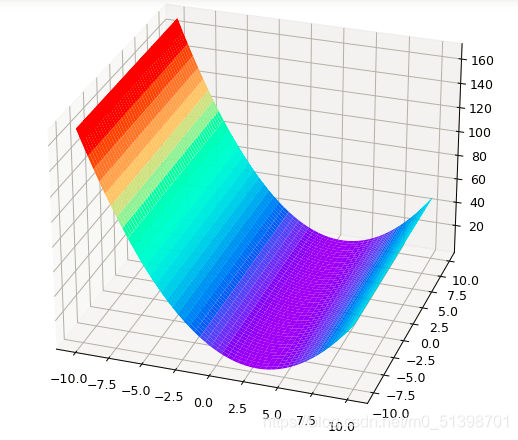
当a保持不变,改变b值的大小,发现当b值从0向正无穷方向增大时,图像开口向上,且弯曲度逐渐增大;当b值从0向负无穷方向减小时,图像逐渐改变弯曲方向,直至开口向下,且弯曲度逐渐增大。
当a=0,b=-0.007时,图像如下:
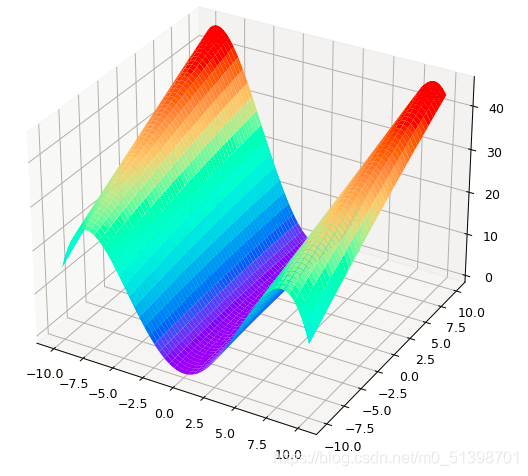
当a=0,b=-0.01时,图像如下:
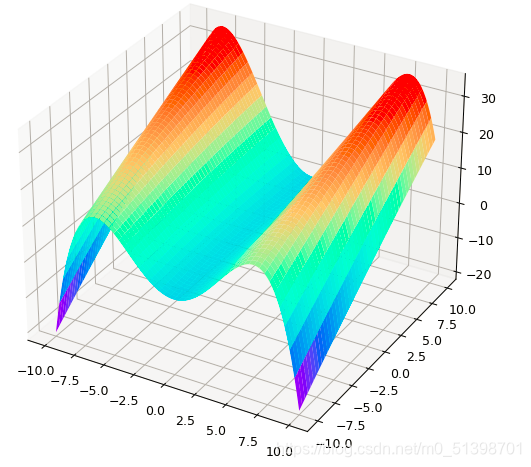
当a=0,b=-0.02时,图像如下:
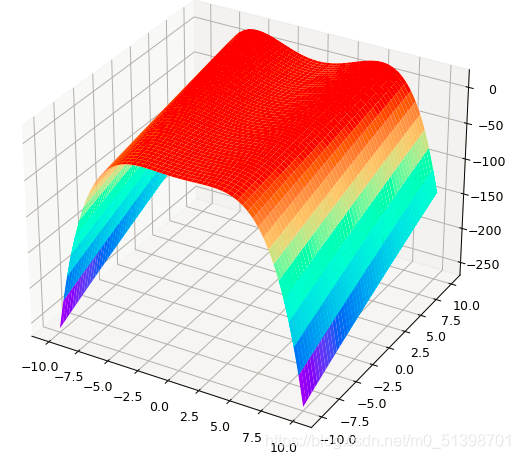
故:参数a可以使图像发生平移,参数b可以改变图像的弯曲程度与弯曲方向。
(2)思路:
先在曲面上生成一个随机点,再通过判断该随机点处的切线的斜率,以某个特定的步长沿着切线函数值减小的方向不断迭代,直至找到该函数的最小值。
代码:
#函数关于x1的偏导
def dfx1(a,b,x_1,x_2):
return -2*a+2*x_1-4*b*x_2*x_1+4*b*x_1**3
#函数关于x2的偏导
def dfx2(a,b,x_1,x_2):
return 2*b*x_2-2*b*x_1**2
Gtadient_Descent_X_1 = []#存放梯度下降的X1坐标
Gtadient_Descent_X_2 = []#存放梯度下降的X2坐标
Gtadient_Descent_z = []
x_1_current = 7 #X初始值
x_2_current =3
a=0
b=0
z_current=f(a,b,x_1_current,x_2_current)
Gtadient_Descent_X_1.append(x_1_current)
Gtadient_Descent_X_2.append(x_2_current)
Gtadient_Descent_z.append(z_current)
learning_rate = 0.5
iter_num = 0 #迭代次数
z_change1 = x_1_current#变换值初始化为X1的初始值
z_change2 = x_2_current#变换值初始化为X2的初始值
while np.abs(z_change1) >= 1e-10 and np.abs(z_change2) >= 1e-10 and iter_num < 500:
x_1_now = x_1_current-learning_rate*dfx1(a,b,x_1_current,x_2_current)
x_2_now = x_2_current-learning_rate*dfx2(a,b,x_1_current,x_2_current)
z_now = f(a,b,x_1_now,x_2_now)
z_change1 =x_1_current-x_1_now
z_change2 = x_2_current-x_2_now
x_1_current = x_1_now
x_2_current = x_2_now
z_current = z_now
iter_num += 1
Gtadient_Descent_X_1.append(x_1_current)
Gtadient_Descent_X_2.append(x_2_current)
Gtadient_Descent_z.append(z_current)
x1_data = np.arange(-10,10,0.2)
x2_data = np.arange(-10,10,0.2)
x1_data,x2_data = np.meshgrid(x1_data,x2_data)
Y = np.array(list(map(lambda t:f(a,b,t[0],t[1]),zip(x1_data.flatten(),x2_data.flatten()))))
Y.shape = x1_data.shape
fig = plt.figure(facecolor='w')
ax = Axes3D(fig)
ax.plot_surface(x1_data,x2_data,Y,rstride = 1,cstride = 1,cmap = plt.cm.jet)
ax.plot(Gtadient_Descent_X_1, Gtadient_Descent_X_2, Gtadient_Descent_z,'bo--')
ax.set_title('最优解为{%.5f,%.5f,%.5f}\n迭代次数为%d'%(x_1_current,x_2_current,z_current,iter_num))
plt.show()
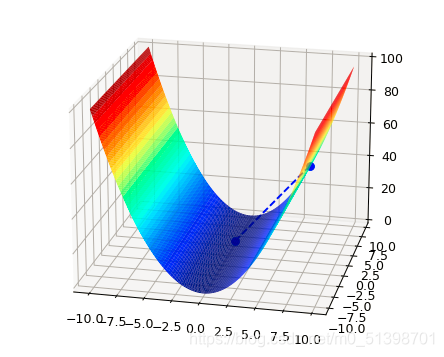
图像如下:
参考:
[1]https://github.com/datawhalechina/ensemble-learning
[2]https://blog.csdn.net/wzyaiwl/article/details/106598209