机器学习数学基础
高等数学与线性代数
-
梯度向量
- 梯度的本意是一个向量(矢量),表示某一函数在该点处的方向导数沿着该方向取得最大值,即函数在该点处沿着该方向(此梯度的方向)变化最快,变化率最大(为该梯度的模)
-
雅克比矩阵(Jacobian矩阵)
假设 F : R n → R m F: \mathbb{R}_{n} \rightarrow \mathbb{R}_{m} F:Rn?→Rm? 是一个从n维欧氏空间映射到到m维欧氏空间的函数。
这个函数由m个实函数组成: y 1 ( x 1 , ? ? , x n ) , ? ? , y m ( x 1 , ? ? , x n ) y_{1}\left(x_{1}, \cdots, x_{n}\right), \cdots, y_{m}\left(x_{1}, \cdots, x_{n}\right) y1?(x1?,?,xn?),?,ym?(x1?,?,xn?) 这些函数的偏导数(如果存在)可以组成一个m行n列的矩阵,这个矩阵就是所谓的雅可比矩阵:
[ ? y 1 ? x 1 ? ? y 1 ? x n ? ? ? ? y m ? x 1 ? ? y m ? x n ] \left[\begin{array}{ccc} \frac{\partial y_{1}}{\partial x_{1}} & \cdots & \frac{\partial y_{1}}{\partial x_{n}} \\ \vdots & \ddots & \vdots \\ \frac{\partial y_{m}}{\partial x_{1}} & \cdots & \frac{\partial y_{m}}{\partial x_{n}} \end{array}\right] ?????x1??y1????x1??ym????????xn??y1????xn??ym???????
可见,梯度向量是雅克比矩阵的特例! -
海森矩阵(Hessian Matrix),是一个多元函数的二阶偏导数构成的方阵,描述了函数的局部曲率。在数学中,海森矩阵是一个自变量为向量的实值函数的二阶偏导数组成的方块矩阵。
假設有一实数函数
f ( x 1 , x 2 , … , x n ) f\left(x_{1}, x_{2}, \ldots, x_{n}\right) f(x1?,x2?,…,xn?)
如果 f f f 所有的二阶偏导数都存在,那么 f f f 的海森矩阵的第 i j i j ij 项,即:
H ( f ) i j ( x ) = D i D j f ( x ) H(f)_{i j}(x)=D_{i} D_{j} f(x) H(f)ij?(x)=Di?Dj?f(x)
其中 x = ( x 1 , x 2 , … , x n ) , x=\left(x_{1}, x_{2}, \ldots, x_{n}\right), x=(x1?,x2?,…,xn?), 即
H ( f ) = [ ? 2 f ? x 1 2 ? 2 f ? x 1 ? x 2 ? ? 2 f ? x 1 ? x n ? 2 f ? x 2 ? x 1 ? 2 f ? x 2 2 ? ? 2 f ? x 2 ? x n ? ? ? ? ? 2 f ? x n ? x 1 ? 2 f ? x n ? x 2 ? ? 2 f ? x n 2 ] H(f)=\left[\begin{array}{cccc} \frac{\partial^{2} f}{\partial x_{1}^{2}} & \frac{\partial^{2} f}{\partial x_{1} \partial x_{2}} & \cdots & \frac{\partial^{2} f}{\partial x_{1} \partial x_{n}} \\ \frac{\partial^{2} f}{\partial x_{2} \partial x_{1}} & \frac{\partial^{2} f}{\partial x_{2}^{2}} & \cdots & \frac{\partial^{2} f}{\partial x_{2} \partial x_{n}} \\ \vdots & \vdots & \ddots & \vdots \\ \frac{\partial^{2} f}{\partial x_{n} \partial x_{1}} & \frac{\partial^{2} f}{\partial x_{n} \partial x_{2}} & \cdots & \frac{\partial^{2} f}{\partial x_{n}^{2}} \end{array}\right] H(f)=?????????x12??2f??x2??x1??2f???xn??x1??2f???x1??x2??2f??x22??2f???xn??x2??2f????????x1??xn??2f??x2??xn??2f???xn2??2f??????????
实际上,Hessian矩阵是梯度向量g(x)对自变量x的雅克比矩阵。 -
最优性条件
设n多元实函数 f ( x 1 , x 2 , ? ? , x n ) f\left(x_{1}, x_{2}, \cdots, x_{n}\right) f(x1?,x2?,?,xn?) 在点 M 0 ( a 1 , a 2 , … , a n ) M_{0}\left(a_{1}, a_{2}, \ldots, a_{n}\right) M0?(a1?,a2?,…,an?) 的邻域内有二阶连续偏导,若有:
? f ? x j ∣ ( a 1 , a 2 , … , a n ) = 0 , j = 1 , 2 , … , n \left.\frac{\partial f}{\partial x_{j}}\right|_{\left(a_{1}, a_{2}, \ldots, a_{n}\right)}=0, j=1,2, \ldots, n ?xj??f?∣∣∣∣?(a1?,a2?,…,an?)?=0,j=1,2,…,n
并且
A = [ ? 2 f ? x 1 2 ? 2 f ? x 1 ? x 2 ? ? 2 f ? x 1 ? x n ? 2 f ? x 2 ? x 1 ? 2 f ? x 2 2 ? ? 2 f ? x 2 ? x n ? ? ? ? ? 2 f ? x n ? x 1 ? 2 f ? x n ? x 2 ? ? 2 f ? x n 2 ] A=\left[\begin{array}{cccc} \frac{\partial^{2} f}{\partial x_{1}^{2}} & \frac{\partial^{2} f}{\partial x_{1} \partial x_{2}} & \cdots & \frac{\partial^{2} f}{\partial x_{1} \partial x_{n}} \\ \frac{\partial^{2} f}{\partial x_{2} \partial x_{1}} & \frac{\partial^{2} f}{\partial x_{2}^{2}} & \cdots & \frac{\partial^{2} f}{\partial x_{2} \partial x_{n}} \\ \vdots & \vdots & \ddots & \vdots \\ \frac{\partial^{2} f}{\partial x_{n} \partial x_{1}} & \frac{\partial^{2} f}{\partial x_{n} \partial x_{2}} & \cdots & \frac{\partial^{2} f}{\partial x_{n}^{2}} \end{array}\right] A=?????????x12??2f??x2??x1??2f???xn??x1??2f???x1??x2??2f??x22??2f???xn??x2??2f????????x1??xn??2f??x2??xn??2f???xn2??2f??????????
则有如下结果:
(1) 当A正定矩阵时, f ( x 1 , x 2 , ? ? , x n ) f\left(x_{1}, x_{2}, \cdots, x_{n}\right) f(x1?,x2?,?,xn?) 在 M 0 ( a 1 , a 2 , … , a n ) M_{0}\left(a_{1}, a_{2}, \ldots, a_{n}\right) M0?(a1?,a2?,…,an?) 处是极小值;
(2) 当A负定矩阵时, f ( x 1 , x 2 , ? ? , x n ) f\left(x_{1}, x_{2}, \cdots, x_{n}\right) f(x1?,x2?,?,xn?) 在 M 0 ( a 1 , a 2 , … , a n ) M_{0}\left(a_{1}, a_{2}, \ldots, a_{n}\right) M0?(a1?,a2?,…,an?) 处是极大值;
(3) 当A不定矩阵时, M 0 ( a 1 , a 2 , … , a n ) M_{0}\left(a_{1}, a_{2}, \ldots, a_{n}\right) M0?(a1?,a2?,…,an?) 不是极值点。
(4) 当A为半正定矩阵或半负定矩阵时, M 0 ( a 1 , a 2 , … , a n ) M_{0}\left(a_{1}, a_{2}, \ldots, a_{n}\right) M0?(a1?,a2?,…,an?) 是“可疑"极值点,尚需要利用其他方法来判定。 -
求带等式约束的优化问题——拉格朗日乘子法
-
基于梯度的优化方法——梯度下降法
-
基于梯度的优化方法——牛顿迭代法
概率论与数理统计
-
贝叶斯公式
定义:设 A 1 , A 2 , ? ? , A n A_{1}, A_{2}, \cdots, A_{n} A1?,A2?,?,An? 是一完备事件组,则对任一事件 B , P ( B ) > 0 , B, P(B)>0, B,P(B)>0, 有
P ( A i ∣ B ) = P ( A i B ) P ( B ) = P ( A i ) P ( B ∣ A i ) ∑ i = 1 n P ( A i ) P ( B ∣ A i ) P\left(A_{i} \mid B\right)=\frac{P\left(A_{i} B\right)}{P(B)}=\frac{P\left(A_{i}\right) P\left(B \mid A_{i}\right)}{\sum_{i=1}^{n} P\left(A_{i}\right) P\left(B \mid A_{i}\right)} P(Ai?∣B)=P(B)P(Ai?B)?=∑i=1n?P(Ai?)P(B∣Ai?)P(Ai?)P(B∣Ai?)?
P ( A i ) P\left(A_{i}\right) P(Ai?) 是在试验以前就已经知道的概率,所以习惯地称为先验概率。试验结果出现了次品(即 B B B 发 生),这时条件概率 P ( A i ∣ B ) P\left(A_{i} \mid B\right) P(Ai?∣B) 反映了在试验以后对 B B B 发生的“来源”(即次品的来源)的各种可能性的大小,通常称为后验概率。 -
概率分布
-
二项分布:
P { X = k } = C n k p k ( 1 ? p ) n ? k P\{X=k\}=C_{n}^{k} p^{k}(1-p)^{n-k} P{X=k}=Cnk?pk(1?p)n?k -
泊松分布:
P { X = k } = λ k k ! e ? λ , k = 0 , 1 , 2 , ? P\{X=k\}=\frac{\lambda^{k}}{k !} e^{-\lambda}, k=0,1,2, \cdots P{X=k}=k!λk?e?λ,k=0,1,2,? -
正态分布:
概率密度函数:
f ( x ) = 1 2 π σ e ? ( x ? μ ) 2 2 σ 2 f(x)=\frac{1}{\sqrt{2 \pi} \sigma} e^{-\frac{(x-\mu)^{2}}{2 \sigma^{2}}} f(x)=2π?σ1?e?2σ2(x?μ)2?
如果一个随机变量 服从均值为 μ , \mu, μ, 标准差为 σ \sigma σ 的正态分布,数学上记作
X ~ N ( μ , σ 2 ) X \sim N\left(\mu, \sigma^{2}\right) X~N(μ,σ2)
-
作业
-
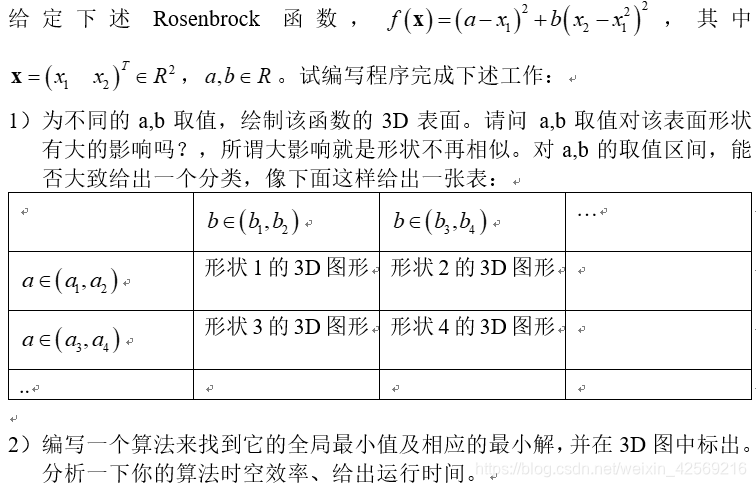
-
# encoding=gbk import numpy as np from mpl_toolkits.mplot3d import Axes3D import matplotlib.pyplot as plt from matplotlib import cm fig=plt.figure() ax = fig.add_subplot(projection='3d') x=np.arange(-1.5,1.5,0.005) # print(x) y=np.arange(-1.5,1.5,0.005) #生成网格点坐标矩阵。 x,y=np.meshgrid(x,y) # print(x) # print(y) def f(x,y): return (a - x) ** 2 + b * (y - x ** 2) ** 2 a = np.random.randint(1, 10) b = np.random.randint(10, 100) print((a, b)) #绘制3D曲面 ax.plot_surface(x,y,f(x,y),cmap = 'rainbow',) dic = {'a':a, 'b':b} ax.set_title(dic) ax.set_xlabel('X') ax.set_xlim(1.5, -1.5,) ax.set_ylabel('Y') ax.set_ylim(1.5, -1.5,) ax.set_zlabel('Z') plt.show()
-
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-2qW5uvtT-1626186074946)(C:\Users\xlli\AppData\Roaming\Typora\typora-user-images\image-20210713160222298.png)]](https://img-blog.csdnimg.cn/20210713222147399.png?x-oss-process=image/watermark,type_ZmFuZ3poZW5naGVpdGk,shadow_10,text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L3dlaXhpbl80MjU2OTIxNg==,size_16,color_FFFFFF,t_70)
a∈(1, 3),b∈(1, 3)时: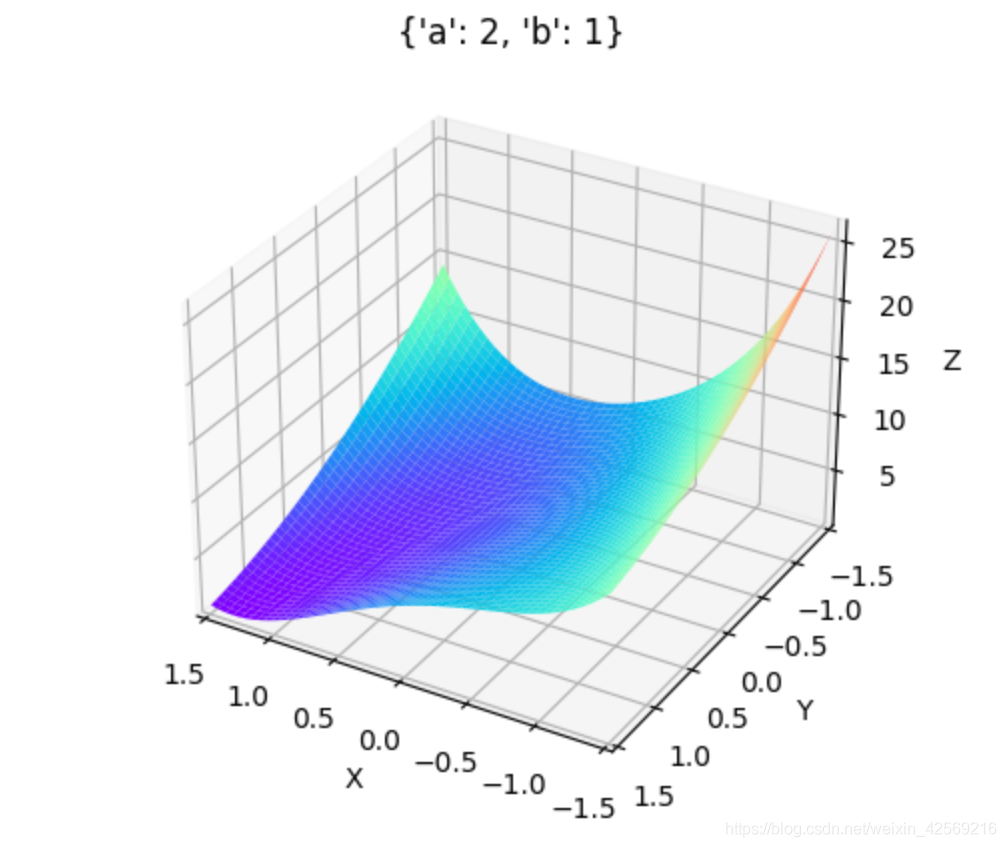
a∈(1, 3),b∈(6, 10)时: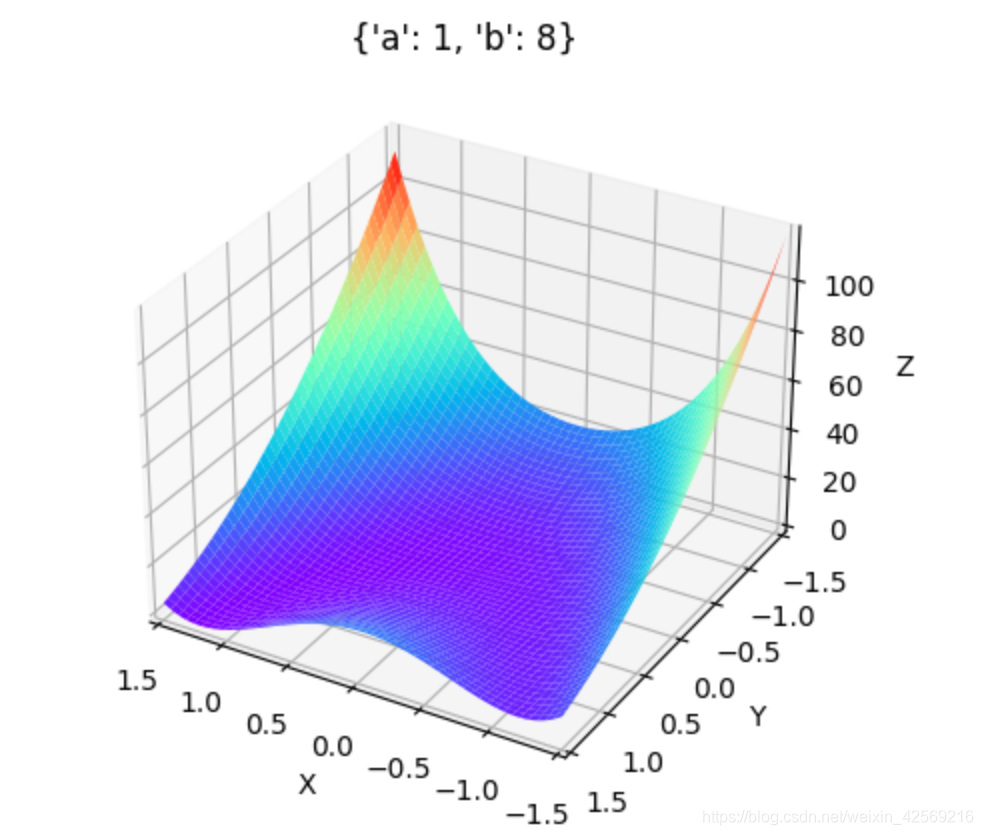
a∈(6, 10),b∈(1, 3)时: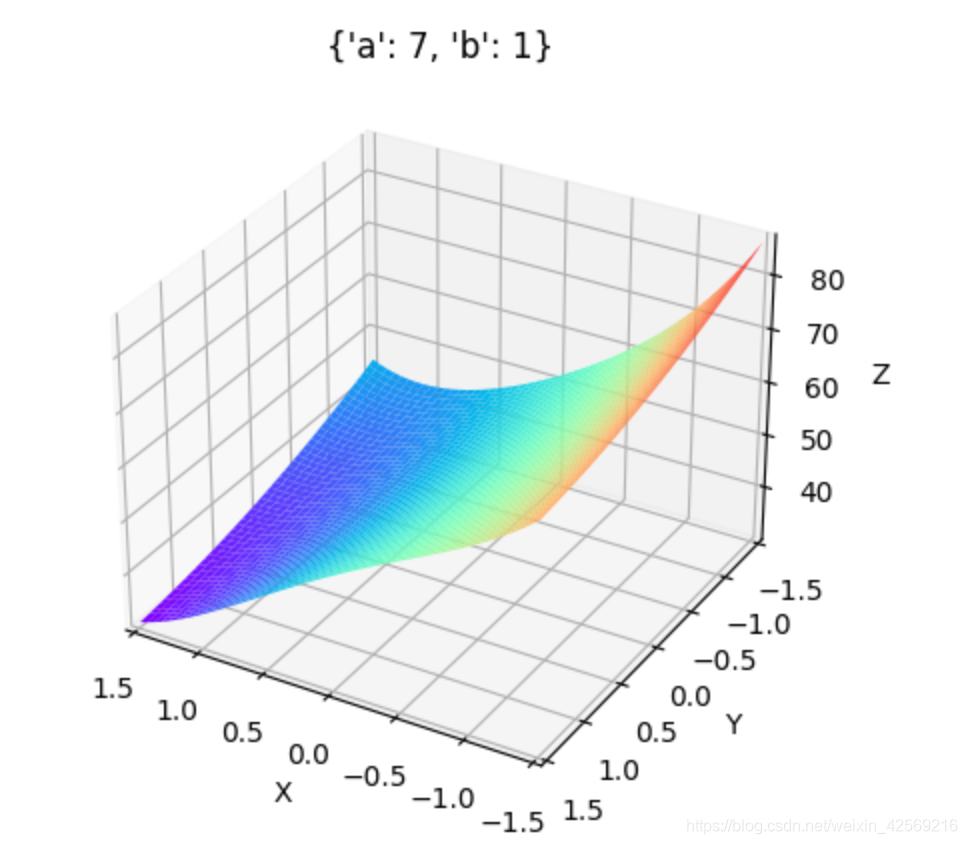
a∈(6, 10),b∈(6, 10)时: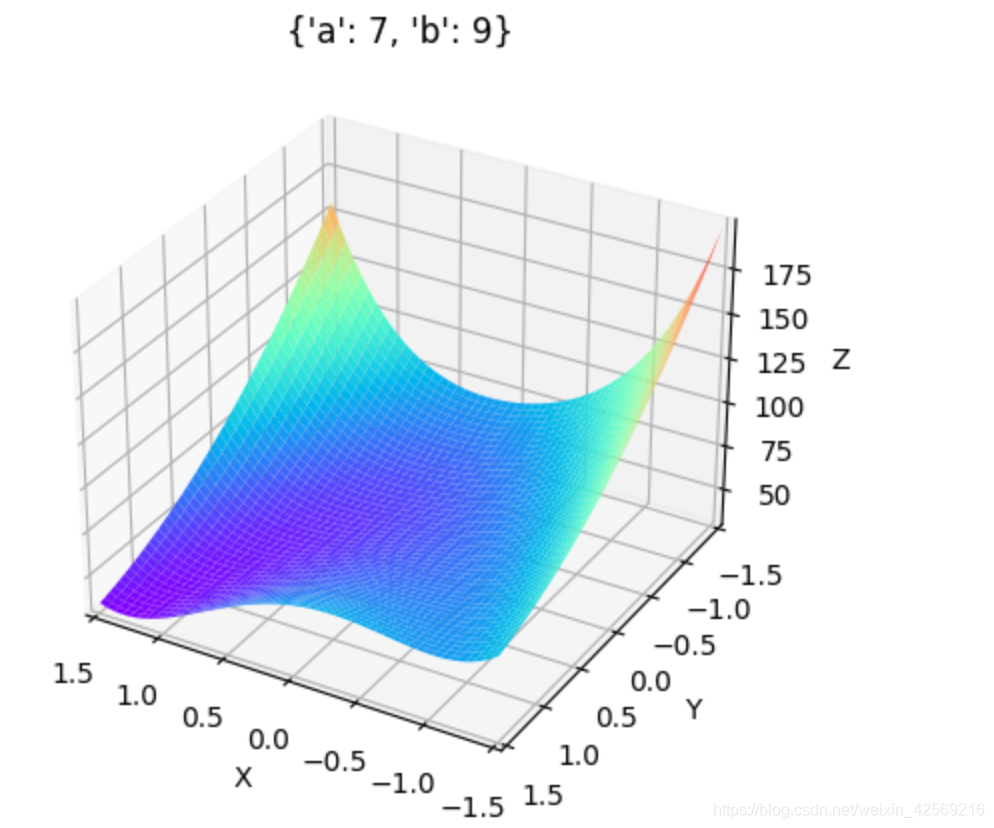
- 找全局最小解
参考资料
https://www.bilibili.com/video/BV1oQ4y1X7ep?p=2
https://github.com/datawhalechina/ensemble-learning