文章目录
本文是学习开源项目‘hands-on data analysis’之后的总结。平台使用jupyter notebook。
项目链接:https://github.com/datawhalechina/ensemble-learning
章节学习视频链接:https://www.bilibili.com/video/BV1oQ4y1X7ep/
高等数学
高等数学中涉及到的基本内容如下:
函数、反函数、复合函数、导数、求导法则(和差积商的求导、复合函数求导、常用初等函数的求导)、高阶导数
多元函数(n维空间)、多元函数的偏导数、梯度向量、雅克比Jacobian矩阵、黑塞Hessian矩阵
函数的极值/最值(最优化问题)、一/多元函数判定极值的方法、求带等式约束的优化问题(拉格朗日乘子法)
泰勒公式、基于梯度的优化方法–梯度下降法、基于梯度的优化方法–牛顿迭代法
考虑到部分内容稍微简单,本文只概述个人认为的部分重点内容。
多元函数的相关概念
-
n维空间
设 n n n 为正整数,用 R n \mathbf{R}^{n} Rn 表示 n n n 元有序实数组 ( x 1 , x 2 , ? ? , x n ) \left(x_{1}, x_{2}, \cdots,\right.\left.x_{n}\right) (x1?,x2?,?,xn?) 的全体所构成的集合,即
R n = R × R × ? × R = { ( x 1 , x 2 , ? ? , x n ) ∣ x i ∈ R , i = 1 , 2 , ? ? , n } . \mathbf{R}^{n}=\mathbf{R} \times \mathbf{R} \times \cdots \times \mathbf{R}=\left\{\left(x_{1}, x_{2}, \cdots, x_{n}\right) \mid x_{i} \in \mathbf{R}, i=1,2, \cdots, n\right\}. Rn=R×R×?×R={(x1?,x2?,?,xn?)∣xi?∈R,i=1,2,?,n}.R n \mathbf{R}^{n} Rn 中的元素 ( x 1 , x 2 , ? ? , x n ) \left(x_{1}, x_{2}, \cdots, x_{n}\right) (x1?,x2?,?,xn?) 有时也用单个字母 x \boldsymbol{x} x 来表示, 即 x = ( x 1 , x 2 , ? ? , x n ) . \boldsymbol{x}=\left(x_{1}, x_{2}, \cdots,\right.\left.x_{n}\right) . x=(x1?,x2?,?,xn?).
当所有的 x i ( i = 1 , 2 , ? ? , n ) x_{i}(i=1,2, \cdots, n) xi?(i=1,2,?,n) 都为零时,称这样的元素为 R n \mathbf{R}^{n} Rn 中的零元,记为0或 O。
在解析几何中,通过直角坐标系, R 2 \mathbf{R}^{2} R2 (或 R 3 \mathbf{R}^{3} R3 )中的元素分别与平面(或空间)中的点(或向量)建立一一对应。
为了在集合 R n \mathbf{R}^{n} Rn 中的元素间建立联系,在 R n \mathbf{R}^{n} Rn 中定义线代运算如下:
设 x = ( x 1 , x 2 , ? ? , x n ) , y = ( y 1 , y 2 , ? ? , y n ) \boldsymbol{x}=\left(x_{1}, x_{2}, \cdots, x_{n}\right), \boldsymbol{y}=\left(y_{1}, y_{2}, \cdots, y_{n}\right) x=(x1?,x2?,?,xn?),y=(y1?,y2?,?,yn?) 为 R n \mathbf{R}^{n} Rn 中任意两个元素, λ ∈ R \lambda \in \mathbf{R} λ∈R,规定:
x + y = ( x 1 + y 1 , x 2 + y 2 , ? ? , x n + y n ) , λ x = ( λ x 1 , λ x 2 , ? ? , λ x n ) \begin{array}{c} \boldsymbol{x}+\boldsymbol{y}=\left(x_{1}+y_{1}, x_{2}+y_{2}, \cdots, x_{n}+y_{n}\right), \\ \lambda \boldsymbol{x}=\left(\lambda x_{1}, \lambda x_{2}, \cdots, \lambda x_{n}\right) \end{array} x+y=(x1?+y1?,x2?+y2?,?,xn?+yn?),λx=(λx1?,λx2?,?,λxn?)?
这样定义了线性运算的集合 R n \mathbf{R}^{n} Rn 称为** n n n 维空间**。n n n维空间中两点间的距离:
R n \mathbf{R}^{n} Rn 中点 x = ( x 1 , x 2 , ? ? , x n ) \boldsymbol{x}=\left(x_{1}, x_{2}, \cdots, x_{n}\right) x=(x1?,x2?,?,xn?) 和点 y = ( y 1 , y 2 , ? ? , y n ) \boldsymbol{y}=\left(y_{1}, y_{2}, \cdots, y_{n}\right) y=(y1?,y2?,?,yn?) 间的距离, 记作 ρ ( x , y ) \rho(\boldsymbol{x}, \boldsymbol{y}) ρ(x,y), 规定
ρ ( x , y ) = ( x 1 ? y 1 ) 2 + ( x 2 ? y 2 ) 2 + ? + ( x n ? y n ) 2 \rho(\boldsymbol{x}, \boldsymbol{y})=\sqrt{\left(x_{1}-y_{1}\right)^{2}+\left(x_{2}-y_{2}\right)^{2}+\cdots+\left(x_{n}-y_{n}\right)^{2}} ρ(x,y)=(x1??y1?)2+(x2??y2?)2+?+(xn??yn?)2? -
二元函数
设 D D D 是 R 2 \mathbf{R}^{2} R2的一个非空子集,称映射 f : D → R f: D \rightarrow \mathbf{R} f:D→R 为定义在 D D D 上的二元函数,常记为 z = f ( x , y ) , ( x , y ) ∈ D z=f(x, y),(x, y) \in D z=f(x,y),(x,y)∈D 或 z = f ( P ) , P ∈ D z=f(P), P \in D z=f(P),P∈D。
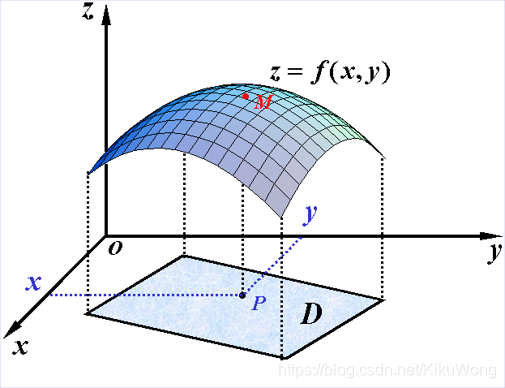
多元函数的偏导数
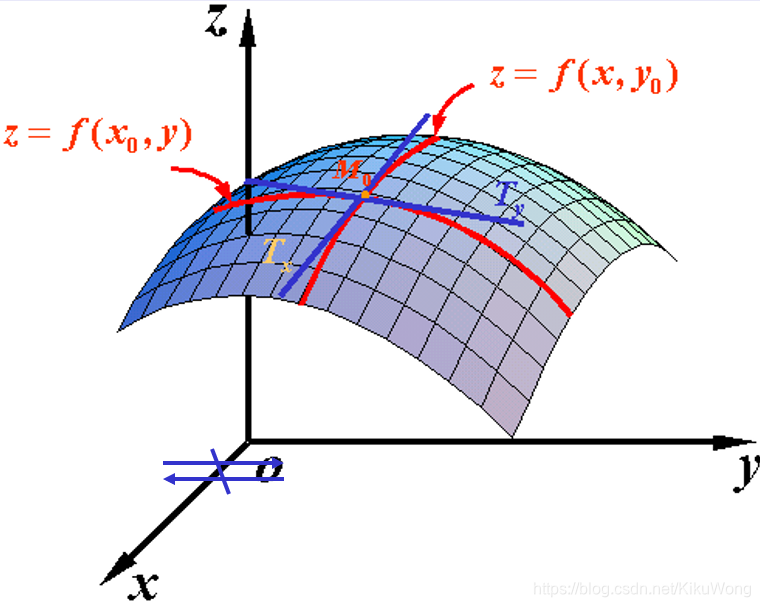
设二元函数 z = f ( x , y ) z=f(x, y) z=f(x,y) 在点 ( x 0 , y 0 ) \left(x_{0}, y_{0}\right) (x0?,y0?) 的某邻域内有定义,如果 lim ? Δ x → 0 Δ x z Δ x \lim\limits_{\Delta x \to 0} \frac{\Delta_{x} z}{\Delta x} Δx→0lim?ΔxΔx?z? 存在,就称其为函数 z = f ( x , y ) z=f(x, y) z=f(x,y)在点( x 0 , y 0 ) \left.x_{0}, y_{0}\right) x0?,y0?) 处对 x x x 的偏导数。
记作 ? z ? x ∣ ( x 0 , y 0 ) \left.\frac{\partial z}{\partial x}\right|_{\left(x_{0}, y_{0}\right)} ?x?z?∣∣?(x0?,y0?)?, ? f ? x ∣ ( x 0 , y 0 ) \left.\frac{\partial f}{\partial x}\right|_{\left(x_{0}, y_{0}\right)} ?x?f?∣∣∣?(x0?,y0?)?,即 ? z ? x ∣ ( x 0 , y 0 ) = lim ? Δ x → 0 Δ x z Δ x = lim ? Δ x → 0 f ( x 0 + Δ x , y 0 ) ? f ( x 0 , y 0 ) Δ x \left.\frac{\partial z}{\partial x}\right|_{\left(x_{0}, y_{0}\right)}=\lim\limits_{\Delta x \to 0} \frac{\Delta_{x} z}{\Delta x} =\lim\limits_{\Delta x \rightarrow 0} \frac{f\left(x_{0}+\Delta x, y_{0}\right)-f\left(x_{0}, y_{0}\right)}{\Delta x} ?x?z?∣∣?(x0?,y0?)?=Δx→0lim?ΔxΔx?z?=Δx→0lim?Δxf(x0?+Δx,y0?)?f(x0?,y0?)? .
梯度向/矢量Gradient
梯度是导数对多元函数的推广,是多元函数对各个自变量偏导数形成的向量,其作用相当于一元函数的导数。
一阶偏导数对一个向量求导,只反映多元函数与一个自变量之间的关系。
梯度则包含了函数对所有自变量的偏导数,综合了对所有自变量的关系。
与一元函数的导数类似,梯度决定了多元函数的单调性和极值。
梯度:某一函数在该点处的方向导数沿着该方向取得最大值,即函数在该点处沿着该方向(此梯度的方向)变化最快,变化率最大(为该梯度的模)。
定义:设二元函数
z
=
f
(
x
,
y
)
z=f(x, y)
z=f(x,y) 在平面区域
D
D
D 上具有一阶连续偏导数,则对于每一个点P
(
x
,
y
)
(x, y)
(x,y)都可定出一个向量
{
?
f
?
x
,
?
f
?
y
}
=
f
x
(
x
,
y
)
i
?
+
f
y
(
x
,
y
)
j
?
\left\{\frac{\partial f}{\partial x}, \frac{\partial f}{\partial y}\right\}=f_{x}(x, y) \vec{i}+f_{y}(x, y) \vec{j}
{?x?f?,?y?f?}=fx?(x,y)i+fy?(x,y)j? ,该函数就称为函数
z
=
f
(
x
,
y
)
z=f(x, y)
z=f(x,y) 在点P
(
x
,
y
)
(x, y)
(x,y)的梯度,记作gradf
(
x
,
y
)
(\mathrm{x}, \mathrm{y})
(x,y) 或
?
f
(
x
,
y
)
\nabla f(x, y)
?f(x,y),即有:
gradf
?
(
x
,
y
)
=
?
f
(
x
,
y
)
=
{
?
f
?
x
,
?
f
?
y
}
=
f
x
(
x
,
y
)
i
?
+
f
y
(
x
,
y
)
j
?
\operatorname{gradf}(\mathrm{x}, \mathrm{y})=\nabla f(x, y)=\left\{\frac{\partial f}{\partial x}, \frac{\partial f}{\partial y}\right\}=f_{x}(x, y) \vec{i}+f_{y}(x, y) \vec{j}
gradf(x,y)=?f(x,y)={?x?f?,?y?f?}=fx?(x,y)i+fy?(x,y)j?
其中
?
=
?
?
x
i
?
+
?
?
y
j
?
\nabla=\frac{\partial}{\partial x} \vec{i}+\frac{\partial}{\partial y} \vec{j}
?=?x??i+?y??j? 称为(二维的)向量微分算子或Nabla算子、梯度算子,
?
f
=
?
f
?
x
i
?
+
?
f
?
y
j
?
\nabla f=\frac{\partial f}{\partial x} \vec{i}+\frac{\partial f}{\partial y} \vec{j}
?f=?x?f?i+?y?f?j? 。
【补充】方向导数与梯度间的关系:
方向导数可看做偏导数的一般化,它可实现任意方向的求导,即自变量沿着某一方向变化时的导数。若该方向指向各个自变量的坐标轴方向,方向导数就是偏导数。
雅克比矩阵(Jacobian矩阵)
雅可比矩阵是向量函数的所有偏导数构成的矩阵,可简化链式法则的表达,在多元函数的换元法中有应用。
假设 F : R n → R m F: \mathbb{R}_{n} \rightarrow \mathbb{R}_{m} F:Rn?→Rm? 是一个从n维欧氏空间映射到到m维欧氏空间的函数(即向量到向量的映射: y = f ( x ) \boldsymbol{y}=f(\boldsymbol{x}) y=f(x))。这个函数由m个实函数组成: y 1 = ( x 1 , ? ? , x n ) , ? ? , y m = ( x 1 , ? ? , x n ) y_{1}=\left(x_{1}, \cdots, x_{n}\right), \cdots, y_{m}=\left(x_{1}, \cdots, x_{n}\right) y1?=(x1?,?,xn?),?,ym?=(x1?,?,xn?) 。
这些函数的偏导数(如果存在)可组成一个m行n列的矩阵,即雅可比矩阵(由多个多元函数梯度组成的矩阵):
[
?
y
1
?
x
1
?
?
y
1
?
x
n
?
?
?
?
y
m
?
x
1
?
?
y
m
?
x
n
]
\left[\begin{array}{ccc} \frac{\partial y_{1}}{\partial x_{1}} & \cdots & \frac{\partial y_{1}}{\partial x_{n}} \\ \vdots & \ddots & \vdots \\ \frac{\partial y_{m}}{\partial x_{1}} & \cdots & \frac{\partial y_{m}}{\partial x_{n}} \end{array}\right]
?????x1??y1????x1??ym????????xn??y1????xn??ym???????
可见,梯度向量是雅克比矩阵的特例!
海森矩阵(Hessian 矩阵)
黑塞矩阵(Hessian Matrix),又称海森矩阵、海瑟矩阵、海塞矩阵等,是由一个多元函数的二阶偏导数构成的方阵,描述了函数的局部曲率。
假设有一实数函数
f
(
x
1
,
x
2
,
…
,
x
n
)
f\left(x_{1}, x_{2}, \ldots, x_{n}\right)
f(x1?,x2?,…,xn?),如果
f
f
f 二阶可导,那么
f
f
f 的海森矩阵为:
H
(
f
)
=
[
?
2
f
?
x
1
2
?
2
f
?
x
1
?
x
2
?
?
2
f
?
x
1
?
x
n
?
2
f
?
x
2
?
x
1
?
2
f
?
x
2
2
?
?
2
f
?
x
2
?
x
n
?
?
?
?
?
2
f
?
x
n
?
x
1
?
2
f
?
x
n
?
x
2
?
?
2
f
?
x
n
2
]
H(f)=\left[\begin{array}{cccc} \frac{\partial^{2} f}{\partial x_{1}^{2}} & \frac{\partial^{2} f}{\partial x_{1} \partial x_{2}} & \cdots & \frac{\partial^{2} f}{\partial x_{1} \partial x_{n}} \\ \frac{\partial^{2} f}{\partial x_{2} \partial x_{1}} & \frac{\partial^{2} f}{\partial x_{2}^{2}} & \cdots & \frac{\partial^{2} f}{\partial x_{2} \partial x_{n}} \\ \vdots & \vdots & \ddots & \vdots \\ \frac{\partial^{2} f}{\partial x_{n} \partial x_{1}} & \frac{\partial^{2} f}{\partial x_{n} \partial x_{2}} & \cdots & \frac{\partial^{2} f}{\partial x_{n}^{2}} \end{array}\right]
H(f)=?????????x12??2f??x2??x1??2f???xn??x1??2f???x1??x2??2f??x22??2f???xn??x2??2f????????x1??xn??2f??x2??xn??2f???xn2??2f??????????
一般,多元函数的混合二阶偏导数与求导次序无关,即 ? 2 f ? x i ? x j = ? 2 f ? x j ? x i \frac{\partial^{2} f}{\partial x_{i} \partial x_{j}}=\frac{\partial^{2} f}{\partial x_{j} \partial x_{i}} ?xi??xj??2f?=?xj??xi??2f?。
实际上,Hessian矩阵是梯度向量g(x)对自变量x的Jacobian矩阵。
多元函数下的极值问题(最优化问题)
设n元实函数
f
(
x
1
,
x
2
,
?
?
,
x
n
)
f\left(x_{1}, x_{2}, \cdots, x_{n}\right)
f(x1?,x2?,?,xn?) 在点
M
0
(
a
1
,
a
2
,
…
,
a
n
)
M_{0}\left(a_{1}, a_{2}, \ldots, a_{n}\right)
M0?(a1?,a2?,…,an?) 的邻域内有二阶连续偏导,若有:
?
f
?
x
j
∣
(
a
1
,
a
2
,
…
,
a
n
)
=
0
,
j
=
1
,
2
,
…
,
n
\left.\frac{\partial f}{\partial x_{j}}\right|_{\left(a_{1}, a_{2}, \ldots, a_{n}\right)}=0, j=1,2, \ldots, n
?xj??f?∣∣∣∣?(a1?,a2?,…,an?)?=0,j=1,2,…,n
并且
A
=
[
?
2
f
?
x
1
2
?
2
f
?
x
1
?
x
2
?
?
2
f
?
x
1
?
x
n
?
2
f
?
x
2
?
x
1
?
2
f
?
x
2
2
?
?
2
f
?
x
2
?
x
n
?
?
?
?
?
2
f
?
x
n
?
x
1
?
2
f
?
x
n
?
x
2
?
?
2
f
?
x
n
2
]
A=\left[\begin{array}{cccc} \frac{\partial^{2} f}{\partial x_{1}^{2}} & \frac{\partial^{2} f}{\partial x_{1} \partial x_{2}} & \cdots & \frac{\partial^{2} f}{\partial x_{1} \partial x_{n}} \\ \frac{\partial^{2} f}{\partial x_{2} \partial x_{1}} & \frac{\partial^{2} f}{\partial x_{2}^{2}} & \cdots & \frac{\partial^{2} f}{\partial x_{2} \partial x_{n}} \\ \vdots & \vdots & \ddots & \vdots \\ \frac{\partial^{2} f}{\partial x_{n} \partial x_{1}} & \frac{\partial^{2} f}{\partial x_{n} \partial x_{2}} & \cdots & \frac{\partial^{2} f}{\partial x_{n}^{2}} \end{array}\right]
A=?????????x12??2f??x2??x1??2f???xn??x1??2f???x1??x2??2f??x22??2f???xn??x2??2f????????x1??xn??2f??x2??xn??2f???xn2??2f??????????
则有如下结果:
(1) 当A为正定矩阵时,
f
(
x
1
,
x
2
,
?
?
,
x
n
)
f\left(x_{1}, x_{2}, \cdots, x_{n}\right)
f(x1?,x2?,?,xn?) 在
M
0
(
a
1
,
a
2
,
…
,
a
n
)
M_{0}\left(a_{1}, a_{2}, \ldots, a_{n}\right)
M0?(a1?,a2?,…,an?) 处是极小值;
(2) 当A为负定矩阵时,
f
(
x
1
,
x
2
,
?
?
,
x
n
)
f\left(x_{1}, x_{2}, \cdots, x_{n}\right)
f(x1?,x2?,?,xn?) 在
M
0
(
a
1
,
a
2
,
…
,
a
n
)
M_{0}\left(a_{1}, a_{2}, \ldots, a_{n}\right)
M0?(a1?,a2?,…,an?) 处是极大值;
(3) 当A为不定矩阵时,
M
0
(
a
1
,
a
2
,
…
,
a
n
)
M_{0}\left(a_{1}, a_{2}, \ldots, a_{n}\right)
M0?(a1?,a2?,…,an?) 不是极值点。
(4) 当A为半正定矩阵或半负定矩阵时,
M
0
(
a
1
,
a
2
,
…
,
a
n
)
M_{0}\left(a_{1}, a_{2}, \ldots, a_{n}\right)
M0?(a1?,a2?,…,an?) 是“可疑"极值点,需用其他方法来判定。
带等式约束的优化问题(拉格朗日乘子法Lagrange Multiplier Method)
二元函数下带等式约束的优化问题:求函数 z = f ( x , y ) z=f(x, y) z=f(x,y) 在条件 φ ( x , y ) = 0 \varphi(x, y)=0 φ(x,y)=0 下的极值。
引入拉格朗日函数 L ( x , y ) = f ( x , y ) + λ φ ( x , y ) L(x, y)=f(x, y)+\lambda \varphi(x, y) L(x,y)=f(x,y)+λφ(x,y) , λ \lambda λ为新引入的自变量,称为拉格朗日乘子。
对所有自变量求偏导,并令其为0,得极值点满足的条件: { L x ( x 0 , y 0 ) = 0 L y ( x 0 , y 0 ) = 0 φ ( x 0 , y 0 ) = 0 \left\{\begin{array}{l}L_{x}\left(x_{0}, y_{0}\right)=0 \\ L_{y}\left(x_{0}, y_{0}\right)=0 \\ \varphi\left(x_{0}, y_{0}\right)=0\end{array}\right. ????Lx?(x0?,y0?)=0Ly?(x0?,y0?)=0φ(x0?,y0?)=0?
更一般的定义如下:
极值问题: min ? x f ( x ) \min\limits_{x} f(x) xmin?f(x) s.t. h i ( x ) = 0 , i = 1 , 2 , … , n h_i(\boldsymbol{x})=0, i=1,2, \ldots, n hi?(x)=0,i=1,2,…,n (s.t.是subject to受限于的意思)
拉格朗日函数为: L ( x , λ ) = f ( x ) + ∑ i = 1 p λ i h i ( x ) L(\boldsymbol{x},\boldsymbol{\lambda})=f(\boldsymbol{x})+\sum\limits_{i=1}^{p} \lambda_{i} h_{i}(\boldsymbol{x}) L(x,λ)=f(x)+i=1∑p?λi?hi?(x)
对拉格朗日乘子函数的所有自变量求偏导数,并令其为0。这包括对 x \boldsymbol{x} x、 λ \boldsymbol{\lambda} λ求导,得到下列方程组:
KaTeX parse error: No such environment: split at position 15: \left\{\begin{?s?p?l?i?t?}? \nabla_{x} f(\…
**求解该方程组即可得到函数的候选极值点。**一般再结合黑塞矩阵,根据该点处黑塞矩阵的正负定性判断是极小值点还是极大值点。拉格朗日乘数法的几何解释:在极值点处目标函数的梯度是约束函数梯度的线性组合 ? x f ( x ) = ? ∑ i = 1 p λ i ? x h i ( x ) \nabla_{x} f(\boldsymbol{x})=-\sum\limits_{i=1}^{p} \lambda_{i} \nabla_{x} h_{i}(\boldsymbol{x}) ?x?f(x)=?i=1∑p?λi??x?hi?(x)
泰勒公式
泰勒公式就是用一个多项式函数去逼近一个给定的函数(即尽量使多项式函数图像拟合给定的函数图像)。
泰勒公式在机器学习中主要应用于梯度迭代
定义:设
n
n
n 是正整数,如果定义在一个包含a的区间上的函数
f
f
f 在
a
a
a 点处
n
+
1
n+1
n+1 次可导,那么对于这个区间上的任意
x
x
x 都有:
f
(
x
)
=
f
(
a
)
0
!
+
f
′
(
a
)
1
!
(
x
?
a
)
+
f
′
′
(
a
)
2
!
(
x
?
a
)
2
+
?
+
f
(
n
)
(
a
)
n
!
(
x
?
a
)
n
+
R
n
(
x
)
=
∑
i
=
0
n
f
(
i
)
(
a
)
i
!
(
x
?
a
)
n
+
R
n
(
x
)
\begin{array}{l} f(x)=\frac{f(a)}{0 !}+\frac{f^{\prime}(a)}{1 !}(x-a)+\frac{f^{\prime \prime}(a)}{2 !}(x-a)^{2}+\cdots+\frac{f^{(n)}(a)}{n !}(x-a)^{n}+R_{n}(x) \\ =\sum\limits_{i=0}^{n} \frac{f^{(i)}(a)}{i !}(x-a)^{n}+R_{n}(x) \end{array}
f(x)=0!f(a)?+1!f′(a)?(x?a)+2!f′′(a)?(x?a)2+?+n!f(n)(a)?(x?a)n+Rn?(x)=i=0∑n?i!f(i)(a)?(x?a)n+Rn?(x)?
其中的多项式称为函数在a处的泰勒展开式,
R
n
(
x
)
R_{n}(x)
Rn?(x) 是泰勒公式的余项。
基于梯度的优化方法–梯度下降法(Python实现举例)
关于梯度下降法具体可参见:梯度下降(Gradient Descent)小结,梯度下降算法(附代码实现)
梯度下降Gradient Descent 的优化公式: x k + 1 = x k ? α ? f ( x ) \boldsymbol{x}_{k+1}=\boldsymbol{x}_{k}-\alpha\nabla f(\boldsymbol{x}) xk+1?=xk??α?f(x) ,其中 x \boldsymbol{x} x 是待求的参数, α \alpha α 是学习率-代表每次优化的步长, f ( x ) f(\boldsymbol{x}) f(x) 是目标函数。
梯度下降是一个迭代的过程,它是渐进的,不是一蹴而就的。
梯度下降法算法过程:
输入:目标函数 f ( x ) f(\boldsymbol{x}) f(x),梯度函数 g ( x ) = ? f ( x ) g(\boldsymbol{x})=\nabla f(\boldsymbol{x}) g(x)=?f(x),计算精度 ε \varepsilon ε
输出: f ( x ) f(\boldsymbol{x}) f(x)的极小值点 x ? \boldsymbol{x^*} x?及相应的极值
取初始值 x 0 ∈ R n \boldsymbol{x_0} \in \mathbf{R}^{n} x0?∈Rn, k = 0 k=0 k=0
计算 f ( x k ) f(\boldsymbol{x_k}) f(xk?)
计算梯度 g k = g ( x k ) g_k=g(\boldsymbol{x_k}) gk?=g(xk?),当 ∣ ∣ g k ∣ ∣ < ε ||g_k||<\varepsilon ∣∣gk?∣∣<ε时,停止迭代,令 x ? = x k \boldsymbol{x^*}=\boldsymbol{x_k} x?=xk?;否则,令负梯度方向 p k = ? g ( x k ) p_k=-g(\boldsymbol{x_k}) pk?=?g(xk?),求 λ k \lambda_k λk?使 f ( x k + λ k p k ) = min ? λ ≥ 0 f ( x k + λ k p k ) f(\boldsymbol{x_k}+\lambda_k p_k)= \min\limits_{\lambda \geq 0} f(\boldsymbol{x_k}+\lambda_k p_k) f(xk?+λk?pk?)=λ≥0min?f(xk?+λk?pk?)
x k + 1 = x k + λ k p k \boldsymbol{x_{k+1}} = \boldsymbol{x_k} + \lambda_k p_k xk+1?=xk?+λk?pk? ,计算 f ( x k + 1 ) f(\boldsymbol{x_{k+1}}) f(xk+1?)
当 ∣ ∣ f ( x k + 1 ) ? f ( x k ) ∣ ∣ < ε ||f(\boldsymbol{x_{k+1}})-f(\boldsymbol{x_{k}})|| < \varepsilon ∣∣f(xk+1?)?f(xk?)∣∣<ε 或 $||\boldsymbol{x_{k+1}} - \boldsymbol{x_k}|| < \varepsilon $ 时,停止迭代,令 x ? = x k + 1 \boldsymbol{x^*}=\boldsymbol{x_{k+1}} x?=xk+1?。
否则,取 k = k + 1 k=k+1 k=k+1,转步骤3
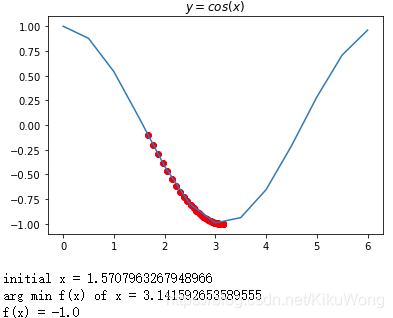
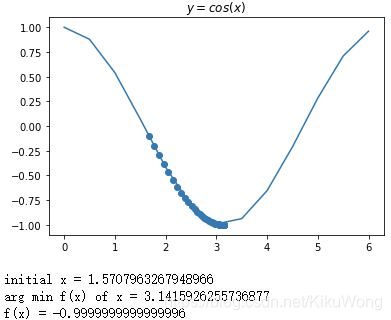
# 使用梯度下降法求函数 𝑦=𝑐𝑜𝑠(𝑥) 在区间 𝑥∈[0,2𝜋] 的极小值点
import numpy as np
import matplotlib.pyplot as plt
import math
# 定义函数:y=cos(x)
def f(x):
return np.cos(x)
# 对定义的函数求导(二元函数时求偏导)-涉及后面的梯度
def df(f, x, delta=1e-4):
'''
求导数的第二种方法:用定义
'''
return (f(x+delta) - f(x-delta)) / (2 * delta)
# 可视化函数:y=cos(x)
xs = np.arange(0, 2*math.pi, 0.5)
plt.plot(xs, f(xs))
# 定义学习率learning rate 和 迭代iterate次数
learning_rate = 0.1
max_loop = 500
# 初始化 x
x = 0.5*math.pi
x_list = [] # 每次更新迭代后将x的值存入其中
# 进行梯度下降法-迭代
for i in range(max_loop):
df_x = df(f,x) # 求导
x = x - learning_rate * df_x # 梯度下降法的公式
x_list.append(x)
# 可视化学习过程
x_list = np.array(x_list)
plt.scatter(x_list, f(x_list), c="r") # 散点
plt.title("$y = cos(x)$")
plt.show()
print('initial x =', x_init) # 打印初始值
print('arg min f(x) of x =', x) # 打印使f(x)最小的x的值
print('f(x) =', f(x)) # 打印f(x)的最小值
import numpy as np
import matplotlib.pyplot as plt
import math
# 定义函数:y=cos(x)
def f(x):
return np.cos(x)
# 对定义的函数求导(二元函数时求偏导)-涉及后面的梯度
def df(f, x, delta=1e-4):
'''
求导数的第二种方法:用定义
'''
return (f(x+delta) - f(x-delta)) / (2 * delta)
# 可视化函数:y=cos(x)
xs = np.arange(0, 2*math.pi, 0.5)
plt.plot(xs, np.array(f(xs)))
# 定义学习率 初始化x
learning_rate = 0.1 # 也可以更改学习率
x = 0.5*math.pi # 随机初始化的x,其他的值也可以
x_list = [] # 每次x更新后把值存在这个列表里面
y_list = [] # 每次更新x后目标函数的值存在这个列表里面
f_current = f_change = f(x)
iter_num = 0
while iter_num <=5000 and f_change > 1e-500: #迭代次数小于5000次或者函数变化小于1e-500次方时停止迭代
iter_num += 1
x = x - learning_rate * df(f, x) # 梯度下降法的公式
tmp = f(x)
f_change = abs(f_current - tmp) # 函数值的变化
f_current = tmp # 迭代后的函数值
x_list.append(x)
y_list.append(f_current)
# 可视化学习过程
plt.scatter(x_list, y_list)
plt.title("$y = cos(x)$")
plt.show()
print('initial x =', x_init) # 打印初始值
print('arg min f(x) of x =', x) # 打印使f(x)最小的x的值
print('f(x) =', f(x)) # 打印f(x)的最小值
基于梯度的优化方法–牛顿迭代法
梯度下降法只利用一阶导数信息,收敛速度慢。通常,利用二阶导数信息可以加快收敛速度,典型代表是:牛顿法、拟牛顿法。
牛顿法在每个迭代点处将目标函数近似为二次函数,然后通过求解梯度为 0 \boldsymbol{0} 0的方程得到迭代方向。
牛顿法在每次迭代时需计算梯度向量与目标函数的黑塞矩阵的逆矩阵,并解一个线性方程组,计算量大且面临何塞矩阵不可逆的问题。拟牛顿法是对它的改进,算法构造出一个正定矩阵作为黑塞矩阵或其逆矩阵的近似。
牛顿法:
牛顿法:利用求解目标函数的极小值的必要条件:
?
f
(
x
)
=
0
\nabla f(\boldsymbol{x})=0
?f(x)=0 ,转化成求使目标函数的梯度(一阶导)为0的参数值。
迭代的公式如下:
KaTeX parse error: No such environment: split at position 8: \begin{?s?p?l?i?t?}? \boldsymbol{x}…
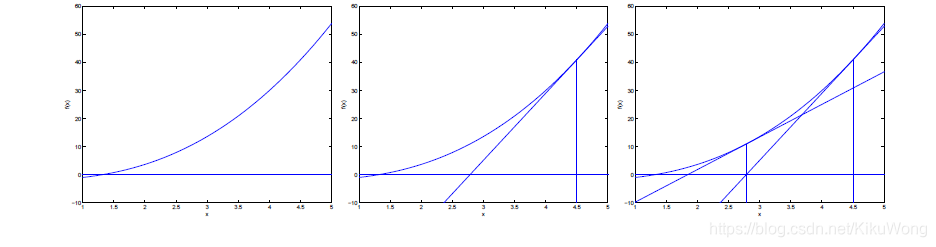
其迭代过程是在当前位置
x
0
x_0
x0?求该函数的切线,该切线和x轴的交点
x
1
x_1
x1?,作为新的
x
0
x_0
x0?,重复这个过程,直到交点和函数的零点重合。此时的参数值就是使得目标函数取得极值的参数值。
其迭代过程如下:
牛顿法算法过程:
输入:目标函数 f ( x ) f(\boldsymbol{x}) f(x),梯度函数 g ( x ) = ? f ( x ) g(\boldsymbol{x})=\nabla f(\boldsymbol{x}) g(x)=?f(x),黑塞矩阵 H ( x ) H(\boldsymbol{x}) H(x) ,计算精度 ε \varepsilon ε
输出: f ( x ) f(\boldsymbol{x}) f(x)的极小值点 x ? \boldsymbol{x^*} x?及相应的极值
- 取初始值 x 0 ∈ R n \boldsymbol{x_0} \in \mathbf{R}^{n} x0?∈Rn, k = 0 k=0 k=0
- 计算梯度 g k = g ( x k ) g_k=g(\boldsymbol{x_k}) gk?=g(xk?)
- 若 ∣ ∣ g k ∣ ∣ < ε ||g_k||<\varepsilon ∣∣gk?∣∣<ε时,则停止计算,得近似解 x ? = x k \boldsymbol{x^*}=\boldsymbol{x_k} x?=xk?
- 计算 H k = H ( x k ) H_k = H(\boldsymbol{x}_{k}) Hk?=H(xk?) ,并求负牛顿方向 p k = ? H k ? 1 g k p_k=-{H_k}^{-1} g_k pk?=?Hk??1gk? # 求 p k p_k pk?较复杂,故有其他改进方法
- x k + 1 = x k + λ k p k \boldsymbol{x_{k+1}} = \boldsymbol{x_k} + \lambda_k p_k xk+1?=xk?+λk?pk?
- 取 k = k + 1 k=k+1 k=k+1,转步骤2
牛顿法和梯度下降法的比较
牛顿法:是通过求解目标函数的一阶导数为0时的参数,进而求出目标函数最小值时的参数。
收敛速度很快。
海森矩阵的逆在迭代过程中不断减小,可以起到逐步减小步长的效果。
缺点:海森矩阵的逆计算复杂,代价比较大,因此有了拟牛顿法。
梯度下降法:是通过梯度方向和步长,直接求解目标函数的最小值时的参数。
越接近最优值时,步长应该不断减小,否则会在最优值附近来回震荡。
线性代数
线性代数中涉及到的基本内容如下:
向量空间、向量及其内积、范数、矩阵及矩阵的秩(数乘、乘法、行列式、余子式、伴随矩阵、可逆矩阵、正交矩阵)、矩阵范数
矩阵的秩 齐次线性方程组及其解空间、特征值与特征向量及矩阵的迹、二次型、合同、正定二次型与Hesse矩阵(黑赛矩阵)
概率论与数理统计
随机事件与概率、条件概率、事件独立性、全概率公式与贝叶斯公式
常见的离散及连续概率分布/概率密度函数/数学期望/方差/协方差
蒙特卡洛随机模拟
极大似然估计、贝叶斯估计
【注】:时间和水平有限,线代及概率知识随后整理。
参考:雷明 《机器学习的数学》
