[人工智能]机器学习笔记 3 —— 朴素贝叶斯

1. naive Bayes

概率估计

朴素贝叶斯法是典型的生成学习方法，生成方法由训练数据学习联合概率分布 $P(X,Y)$，然后求得后验概率分布 $P(Y|X)$。具体来说，利用训练数据学习条件概率 $P(X|Y)$ 和 先验概率 $P(Y)$，得到联合概率分布：

$$P(X,Y)＝P(Y)P(X|Y)$$

概率估计方法可以是极大似然估计或贝叶斯估计，贝叶斯估计 是在 极大似然估计 上加上一个参数 $\lambda$，如 $\lambda =1$：

$$P(Y=c_k)=\frac{\sum _{i=1}^{N}I(y_i=c_k)+\lambda }{N+K\lambda }$$

$$P(X^{(j)}=a_{jl}|Y=c_k)=\frac{\sum _{i=1}^{N}I(x_i^{(j)}=a_{jl},y_i=c_k)+\lambda }{\sum _{i=1}^{N}I(y_i=c_k)+S_j\lambda }$$

其中，$S_j$ 为输入的第 j 个特征的所有取值可能性，$K$ 为类的总数，这样可以避免概率为零的情况。

基本假设

朴素贝叶斯法的基本假设是 条件独立性：

$$\begin{array}{rl}P(X& =x|Y=c_k)=P\left(X^{(1)}=x^{(1)},?,X^{(n)}=x^{(n)}|Y=c_k\right)\\ & =\prod _{j=1}^{n}P\left(X^{(j)}=x^{(j)}|Y=c_k\right)\end{array}$$

这是一个较强的假设，这也是称为朴素的原因。由于这一假设，模型包含的条件概率的数量大为减少，因而朴素贝叶斯法高效，且易于实现，缺点是分类的性能不一定很高。

策略 —— 后验概率最大化

朴素贝叶斯法利用贝叶斯定理与学到的联合概率模型进行分类预测。

$$P(Y|X)=\frac{P(X,Y)}{P(X)}=\frac{P(Y)P(X|Y)}{{\sum }_{Y}P(Y)P(X|Y)}$$

将输入 $x$ 分到后验概率最大的类 $y$ ：

$$y=\arg \underset{c_k}{\max }P\left(Y=c_k\right)\prod _{j=1}^{n}P\left(X_j=x^{(j)}|Y=c_k\right)$$

后验概率最大等价于0-1损失函数时的期望风险最小化。

模型

模型：高斯模型、多项式模型、伯努利模型

当特征值的取值情况有限时，可以计算特征值的所有可能取值的概率；但当特征的取值是 连续 的情况下，需要计算分类到不同类时，每一个特征取值的概率密度函数，常把特征的取值假设为 高斯概率密度函数 PDF

2. GaussianNB 高斯朴素贝叶斯

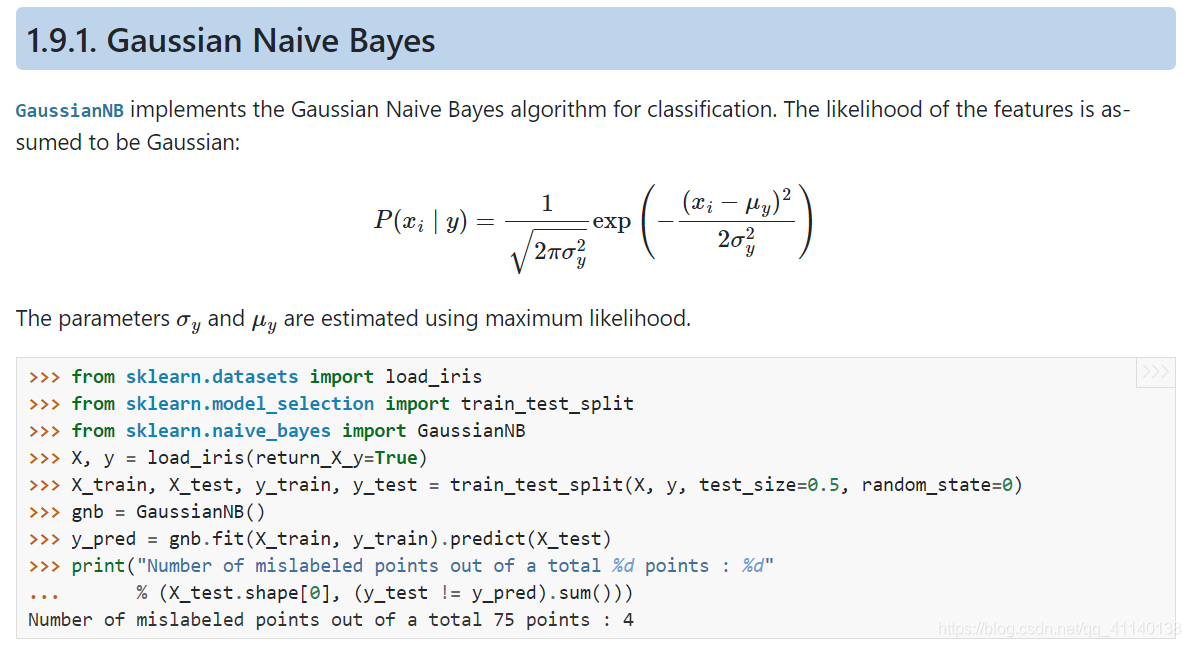
GaussianNB 高斯朴素贝叶斯假特征的取值的可能性为高斯概率密度函数：

$$P(x_i\mid y)=\frac{1}{\sqrt{2\pi {\sigma }_y^2}}\exp \left(?\frac{(x_i?{\mu }_y{)}^2}{2{\sigma }_y^2}\right)$$

其中，$x_i$为独立特征向量 $x_1,x_2,...,x_n$ 中的第 $i$ 个特征，${\sigma }_y$ 代表 $x$ 被分类到 $y$ 类时，$x_i$ 的方差，${\mu }_y$ 代表$x_i$ 的均值，两个参数均为最大似然估计计算得到的。

2.1 数据集预处理

使用 iris 鸢尾花数据集，20% 的数据用于测试：

import math
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split

def create_data():
	iris = load_iris()
	df = pd.DataFrame(data=iris.data, columns=iris.feature_names)
	df['label'] = iris.target
	df.columns = ['sepal length', 'sepal width', 'petal length', 'petal width', 'label']
	data = np.array(df.iloc[:100, :])
	return data[:, :-1], data[:, -1]

X, y = create_data()
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2)

2.2 构建 NaiveBayes 模型

使用 naive bayes 分类的步骤如下：

1. 根据 label 标签对数据集分组，label 有多少种取值就把数据分为多少组
2. 对于 label 相同的所有数据，计算每一个特征的均值和方差，用于计算对于的特征取值的概率密度函数（如下图所示）
   
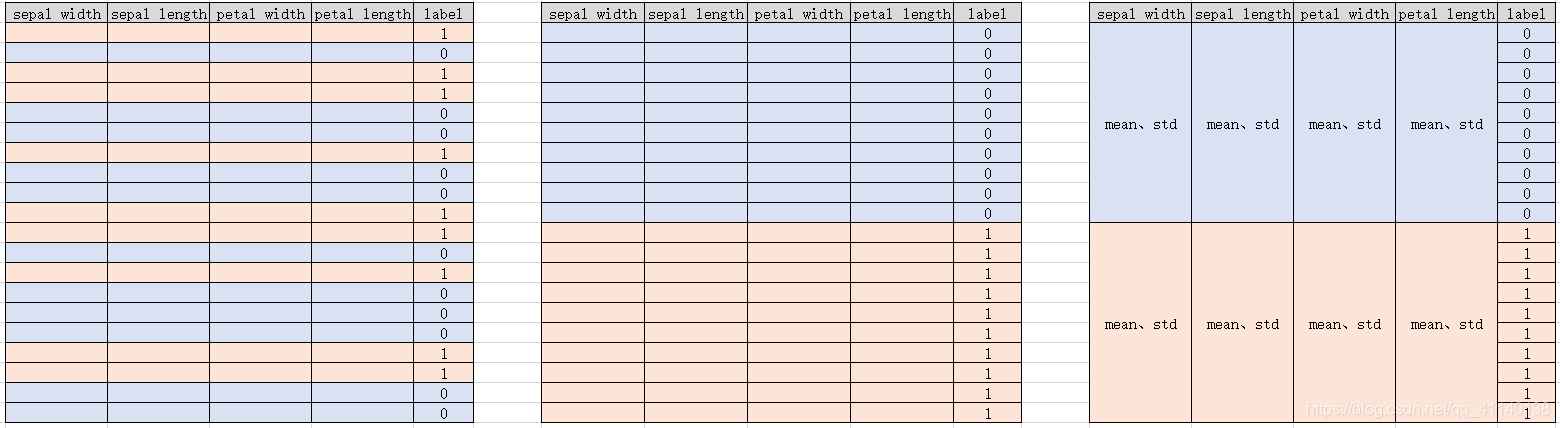
3. 根据输入的特征向量，计算分类到每一类对于的概率
4. 选择概率最大的类作为目标结果

Python 程序如下：

class NaiveBayes:
	def __init__(self):
		self.model = None

	# Gaussian probability density function
	def gaussian_pdf(self, x, mean, std):
		exp_part = math.exp(-(math.pow(x-mean, 2))/(2*math.pow(std, 2)))
		return 1/(math.sqrt(2*math.pi*std)) * exp_part

	# caculate mean and std for each feature of each label
	def summarize(self, train_data):
		summeries = [(np.mean(i), np.std(i)) for i in zip(*train_data)]
		return summeries

	def fit(self, X, y):
		# classify features by labels
		labels = list(set(y))
		data = {label: [] for label in labels}
		for features, label in zip(X, y):
			data[label].append(features)

		# conditional probability
		self.model = {
			label: self.summarize(features)
			for label, features in data.items()
		}
		return 'gaussian naive Bayes train done!'

	def caculate_probabilities(self, input_data):
		probabilities = {}
		for label, value in self.model.items():
			probabilities[label] = 1
			for i in range(len(value)):
				mean, std = value[i]
				probabilities[label] *= self.gaussian_pdf(
					input_data[i], mean, std)
		return probabilities

	def predict(self, X_test):
		label = sorted(
			self.caculate_probabilities(X_test).items(),
			key=lambda x: x[-1])[-1][0]
		return label
	
		def score(self, X_test, y_test):
		right = 0
		for X, y in zip(X_test, y_test):
			if y == self.predict(X):
				right += 1
		return right / float(len(X_test))

其中，self.model 存储了划分到每一类的所有特征值的均值方差，相当于存储了每一个特征取值的条件概率（选择的类为条件）；

程序中有 zip() 函数，它可以合并两个列表，*运算符可以拆开列表：

print(*[1, 2, 3])   # 1 2 3

a = zip([0, 1, 2], [3, 4, 5])
print(list(a))      # [(0, 3), (1, 4), (2, 5)]

a = [[0, 1], [2, 3], [4, 5]]
print(list(zip(*a)))    # [(0, 2, 4), (1, 3, 5)]

2.3 训练与预测

# train
model = NaiveBayes()
model.fit(X_train, y_train)
# predict
print(model.score(X_test, y_test))

得到的结果为 1.0，准确率 100% 🍻

3. scikit - learn 实例

scikit-learn 中定义了 Gaussian Naive bayes:

from sklearn.datasets import load_iris
from sklearn.naive_bayes import GaussianNB
from sklearn.model_selection import train_test_split

X, y = load_iris(return_X_y=True)
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2)

clf = GaussianNB()
clf.fit(X_train, y_train)
print(clf.score(X_test, y_test))    # 0.933
print(clf.predict([X_test[0]]))     # [1]

其中 sklearn.datasets.load_iris 的参数 return_X_y 为 True 表示返回 (data, target) 而不是一个对象，此时训练集和数据集包含了 3 类鸢尾花，此时的预测成功率为 93.3%

完结 🍻

REFERENCE

• 李航统计学习方法
• lihang-machine-learning-code
• scikit learn