How to Build a Graph-Based Deep Learning Architecture in Traffic Domain: A Survey

1. 文章概述

1.1 本文主要内容

我们首先给出基于图的交通问题的公式，并从各种交通数据集构建图。
分解这些基于图的架构，讨论它们使用的深度学习技术，阐明每种技术在流量任务中的应用
总结了一些常见的流量挑战以及相应的基于图的深度学习解决方案
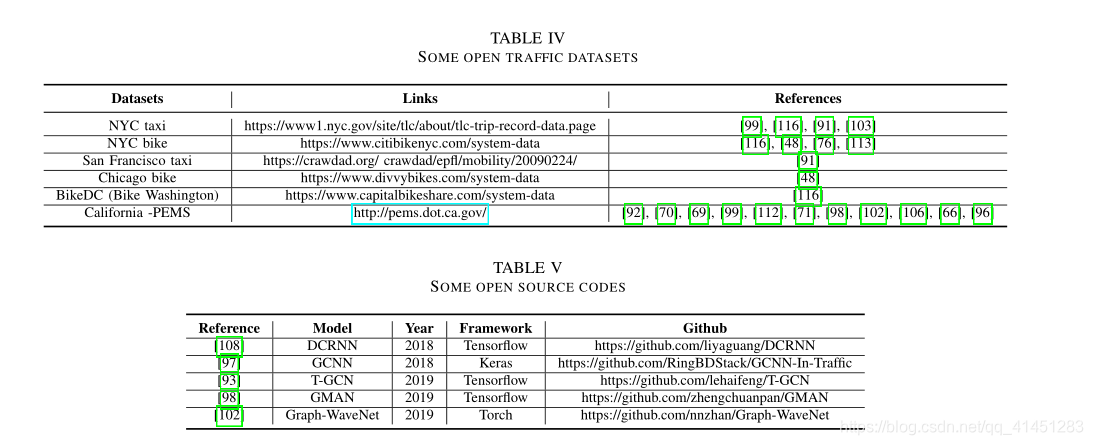
提供了基准数据集、开源代码和未来的研究方向

1.2 在流量预测领域的一些方法

基于统计学的方法：统计学方法基于对数据是线性平稳的假设，该假设不符合实际，使以效果不佳
基于传统机器学习：传统机器学习方法浅层的结果和分离学习的方法在特征捕捉方面效果不佳，且需要手工处理数据在大数据环境下不太适用。
基于深度学习方法：主要是CNN+RNN，使用CNN捕捉空间依赖，使用RNN捕捉时间依赖。但是由于交通网络在时间情况下通常是图结构的，所以使用CNN捕捉不是最佳的。
基于图神经网络：许多现有的工作将GNNs结合到深度学习架构中，以捕捉空间依赖性，且表现出更好的

1.3 挑战和技术回顾

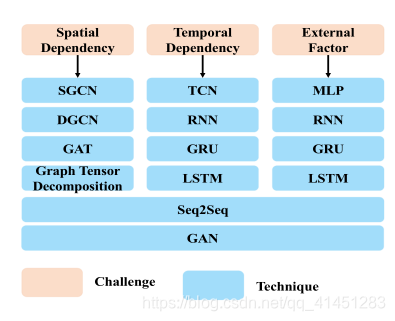
在这里插入图片描述

主要挑战：时间和空间依赖性的捕捉和外部因素

时空依赖性：在预测一个地区的交通状况时需要考虑周围地区的交通状况和起一个时间段的交通状况

额外的因素：如节假日、天气等因素也会对交通预测产生影响

2. 图的构建

2.1 节点及节点特征的构建

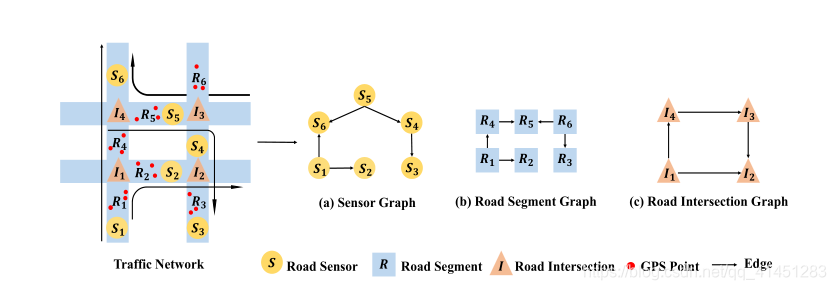
在这里插入图片描述

（1）节点和节点特征构造：

Sensors Datasets：该类型数据库分为两种
- A sensor graph：传感器代表一个节点，该节点的特征是由其对应的传感器收集的流量测量值
- **A road segment graph **：一个路段代表一个节点，该节点的特征是对应路段所有传感器的平均交通测量值
GPS Datasets：全球定位系统轨迹数据集通常是由一个城市某段时间内的出租车数量生成的。
- A road segment graph：其中路段代表一个节点，该节点的特征是由其对应路段上的所有GPS点记录的平均交通测量值
- A road intersection graph：其中道路交叉口代表一个节点，该节点的特征是通过它的交通测量的总和
Rail-hailing Datasets ：这些数据集记录了各个城市一段时间内的汽车/出租车/自行车需求订单。该类型数据将城市讽刺大小相等的网格，每个网格代表一个点，每个点的特征是给定时间间隔内相应区域中的订单数量
Transactions Datasets：这些数据集由部署在公共交通网络(如地铁网络和公交网络)中的自动售检票系统收集。每个车站被视为一个节点，车站的特征通常包含离开的乘客数量。

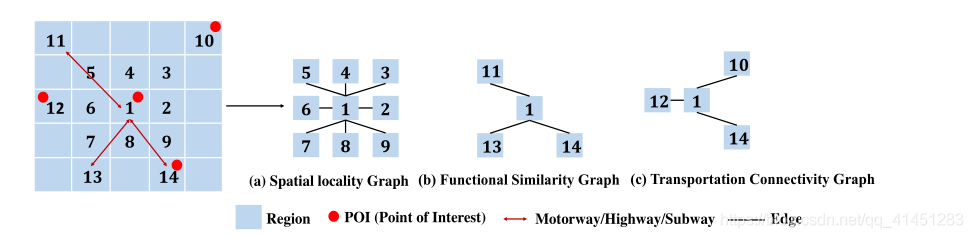
在这里插入图片描述

（2）邻接矩阵构造

Fixed Matrix：许多工作假设节点之间的相关性是固定的，不会随着时间而改变。因此，设计了一个固定的矩阵，并且在整个实验过程中保持不变。

Distance matrix：根据几何距离测量节点之间的接近度。有些工作使用阈值高斯核来定义邻接矩阵，其中d_ij为两点间距离，

$\mathbf{a}_{i j}=\left\{\begin{array}{l} \exp \left(-\frac{\mathbf{d}_{i j}^{2}}{\sigma^{2}}\right), i \neq j \text { and } \mathbf{d}_{i j} \geq \epsilon \\ 0, i=j \text { or } \mathbf{d}_{i j}<\epsilon \end{array}\right.$

Functional similarity matrix ：衡量两个节点在功能上是否相似，共享相似功能的地区可能有相似的需求模式，所以在具有相同兴趣点的区域之间建立边(此处论文中给定的图应该是给反了)
Transportation connectivity matrix:距离遥远但是交通方便的两点之间（如通高速）应该建边

Dynamic Matrix：由于有缺陷的先验知识或不完整的数据，预定义矩阵不一定反映节点之间的真正依赖关系。在一些实验中已经证明该矩阵能更好的捕捉隐藏的空间特征。这种自适应矩阵通过数据进行学习。

Evolving Matrix：在某些情况下，图形结构会随着时间的推移而演变。进化的拓扑结构被结合到模型中以捕捉这种动态空间变化。

3. 深度学习技术回顾

3.1 GNN:

在交通预测领域主要使用的是ConvGNNs，ConvGNNs主要有两种卷积方法一种是基于谱理论的图卷积，一种是基于空间的图卷积。基于空间的图卷积中最近的主要方法是使用扩散卷积。spectral graph convolution (SGC)只能用于无向图的， diffusion graph convolution (DGC) 既可以用于有向图也可以用于无向图。

3.1.1 spectral-based convolutions

三种常用拉普拉斯矩阵：（1）$ L=D-A$ （2） $L=D^{-1/2}LD^{-1/2}=I-D^{-1/2}AD^{-1/2}$ (3) $L=D^{-1}L$

为什么使用拉普拉斯矩阵：（1）拉普拉斯矩阵是对称矩阵可以进行特征分解（2）由于卷积在傅里叶域计算相对简单，为了在graph上做傅里叶变换需要找到连续的正交基对应于傅里叶变换的基，因此要使用拉普拉斯矩阵的特征向量

由卷积定理：函数卷积的傅里叶变换是函数傅立叶变换的乘积，所以对图的特征f和卷积核g可以表示为 $f*g=U((U^Tg)(U^Tf))$ 如果将 $U^Tg$ 看成一个整体 $\theta$ 可以写成 $f*g=U{\Theta}U^Tf$ 。这就是基于谱理论的卷积操作，但是这种操作的时间复杂度为 $O(N^2)$ 太过耗时。

在之后的改进中Defferrard et al通过将 $\Theta$ 限制为 $\Theta=\sum_{i=1}^{K-1}\theta_k\Lambda^K$ ，则卷积表达式可以表示为 $\sum_{k=0}^{K-1}\theta_kU\Lambda U^Tx=\sum_{k=0}^{K-1}\theta_kL^kx$ ，并通过Chebyshev多项式 $T_k(x)$ 逼近 $L_k$ 最终卷积公式为： $\sum_{k=0}^{K-1}\theta_kT_k(\tilde{L})x$ ，其中 $\tilde{L}=\frac{2}{\lambda_{max}}L-I_N$ (这里是为了满足Chebyshev多项式的输入要在[ ? 1 , 1 ] 之间)，通过这种方法可以将时间复杂度降为 $O (K ∣ E ∣)$ 。

3.1.2 spatial-based convolutions

扩散卷积神经网络（DCNN）[25]将图形卷积视为扩散过程。它假设信息以一定的转移概率从一个节点传输到其相邻节点之一，以便信息分布在几轮之后达到平衡。卷积层定义如下：
$\begin{aligned} Y_{j} &=\boldsymbol{\rho}\left(\sum_{k=0}^{\mathrm{K}-1} \sum_{i=1}^{\mathbf{F}_{\mathbf{I}}}\left(\theta_{k, 1, i, j}\left(\mathbf{D}_{\mathbf{O}}^{-1} \mathbf{A}\right)^{k}+\theta_{k, 2, i, j}\left(\mathbf{D}_{\mathbf{I}}^{-1} \mathbf{A}^{T}\right)^{k}\right) X_{i}\right) \\ Y &=\boldsymbol{\rho}\left(\sum^{\mathbf{K}-1}\left(\mathbf{D}_{\mathrm{O}}^{-1} \mathbf{A}\right)^{k} X W_{k 1}+\left(\mathbf{D}_{\mathbf{I}}^{-1} \mathbf{A}^{T}\right)^{k} X W_{k 2}\right) \end{aligned}$
其中 $D_o$ 为出度矩阵 $D_I$ 为入度矩阵。状态迁移矩阵定义为 $D^{-1}A$

3.1.3 图卷积在交通领域的应用

Guo et al.重新定义了的注意机制，以自适应地捕捉交通网络中的动态相关性；
Y u .等人通过扫描图上的K阶邻居和时间轴上的Kt邻居，在没有填充的情况下，在空间和时间维度上推广了SGC

3.2 RNN

3.2.1 LSTM

为了克服梯度消失问题，LSTM引入门控机制
$\begin{aligned} i_{t} &=\sigma\left(\left[\mathbf{H}_{t-1}, \mathbf{X}_{t}\right] \cdot W_{i}+b_{i}\right) \\ o_{t} &=\sigma\left(\left[\mathbf{H}_{t-1}, \mathbf{X}_{t}\right] \cdot W_{o}+b_{o}\right) \\ f_{t} &=\sigma\left(\left[\mathbf{H}_{t-1}, \mathbf{X}_{t}\right] \cdot W_{f}+b_{f}\right) \\ \mathbf{C}_{t} &=f_{t} \odot \mathbf{C}_{t-1}+i_{t} \odot \tanh \left(\left[\mathbf{H}_{t-1}, \mathbf{X}_{t}\right] \cdot W_{c}+b_{c}\right) \\ \mathbf{H}_{t} &=o_{t} \odot \tanh \left(\mathbf{C}_{t}\right) \end{aligned}$

3.2.2 GRU

GRU是LSTM的变种，LSTM有输入门，输出门，遗忘门而GRU只有两个门，减少了参数，从而缩短训练时间
$\begin{aligned} r_{t} &=\boldsymbol{\sigma}\left(\left[\mathbf{H}_{t-1}, \mathbf{X}_{t}\right] \cdot W_{r}+b_{r}\right) \\ u_{t} &=\boldsymbol{\sigma}\left(\left[\mathbf{H}_{t-1}, \mathbf{X}_{t}\right] \cdot W_{u}+b_{u}\right) \\ \tilde{\mathbf{H}}_{t} &=\tanh \left(r_{t} \odot\left[\mathbf{H}_{t-1}, \mathbf{X}_{t}\right] \cdot W_{h}+b_{h}\right) \\ \mathbf{H}_{t} &=u_{t} \odot \mathbf{H}_{t-1}+\left(1-u_{t}\right) \odot \tilde{\mathbf{H}}_{t} \end{aligned}$

3.2.3 RNN在交通领域的应用

Spa-tiotemporal multi-graph convolution network for ride-hailing demand forecasting：将上下文信息，即包含相关区域信息的SGCN输出，合并到注意力操作中，以对不同时间戳处的观测值之间的相关性建模
Gated residual recurrent graph neural networks for traffic prediction：通过在输入中嵌入外部属性来考虑外部因素，并且通过残差路径将先前的隐藏状态添加到下一个隐藏状态，这能使GRU对对交通历史观测中的突然变化更加敏感和鲁棒
Y u .等人[105]通过改变隐藏状态将一个扩张的跳跃连接插入GRU，由 $H_t=GRU([H_{t-1},X_t])$ 变为 $H_t=GRU([H_{t-s},X_t])$
用谱图卷积(SGC)或扩散图卷积(DGC)来代替RNNs隐藏层中的矩阵乘法，以联合捕获时空相关性

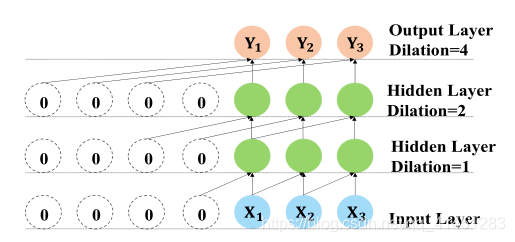
3.3 TCN

3.3.1 Sequence Modeling and 1-D TCN

TCN的论文链接

TCN是结合因果卷积、膨胀卷积的结合操作：
$\mathbf{y}_{t}=\Theta *_{\mathcal{T}^{\mathbf{d}}} \mathbf{x}_{t}=\sum_{k=0}^{\mathbf{K}-1} w_{k} \mathbf{x}_{t-\mathbf{d} k}$
$_{\mathcal{T}^{\mathbf{d}}}$ 是扩张率为d的dilated causal操作，在大部分工作中TCN能有比LSTM更好的效果。

在这里插入图片描述

4. 交通领域的四大挑战

4.1 空间依赖的捕捉

Spatial Locality：空间局部性是指相邻区域通常彼此高度相关。
Multiple Relationships: 位置属性侧重于空间邻近性，但目标区域可以通过各种非欧几里德关系(如功能相似性、交通连通性、语义邻居)与远处区域相关联
Global Connectivity：指不同地区的交通状况在整个网络规模上相互影响。捕捉全局连通性的一种流行方法是将交通网络中不断变化的交通状况建模为发生在网络规模上的扩散过程，该扩散过程由转移矩阵的幂级数表示。

4.2 时间依赖

Multi-timescale：一些从多时间尺度的角度提取时间相关性。时间依赖被分解成最近的，每天的，和每周的依赖。Attention based spatial-temporal graph convolutional networks for traffic flow forecasting设置三个具有相同结构的并行组件来分别建模这三个时间属性。
Different Weights：一些著作认为，历史观测和未来观测之间的相关性在不同的时间片上是不同的。