最近简单看了下图卷积,由于图卷积需要用到傅里叶变换,拉普拉斯矩阵等数据知识,但是之前没有学过,因此没有深入地从严谨数学推导角度出发看一遍图卷积,而是看了白话的图卷积操作的理解,具体可以看这篇文章。之后结合pyg的官网和网上的介绍实现了一下ENZYMES这个数据集的图卷积预测。ENZYMES数据集包含着600张图,每张图有一个label,label共有6种可能的属性,分别是0-5,用540张图做训练集训练,预测最后60张图的label,使用的网络是根据官网的那个简单的网络修改的。
下面的代码主要包括这些部分:
- ENZYMES数据集介绍分析和可视化;
- GNN网络构建;
- 模型的训练及预测;
训练使用的是dataloader这个class,每次喂batch个图进去,训练epoch轮,然后去预测。
import torch
import torch.nn.functional as F
from torch_geometric.nn import GCNConv
from torch_geometric.datasets import Planetoid
from torch_geometric.datasets import TUDataset
import networkx as nx
import torch_geometric
import matplotlib.pyplot as plt
from torch_geometric.data import DataLoader
import torch_geometric.nn as pyg_nn
import numpy as np
1.加载数据并理解数据集
# 加载Cora数据集.(自动帮你下载)
dataset = TUDataset(root='C:/Users/MI/Desktop/GCN/', name='ENZYMES')
dataset
Downloading https://www.chrsmrrs.com/graphkerneldatasets/ENZYMES.zip
Extracting C:\Users\MI\Desktop\GCN\ENZYMES\ENZYMES.zip
Processing...
Done!
ENZYMES(600)
dataset.num_features
3
dataset.num_classes
6
print(len(dataset))
data = dataset[0]
data
# edge_index代表的是边矩阵,是2行,74564列。x是特征矩阵,19580行,3列,说明有19580个node,y是标签。
600
Data(edge_index=[2, 168], x=[37, 3], y=[1])
# Node feature matrix with shape [num_nodes, num_node_features]
print(data.x)
print(data.x.shape)
tensor([[1., 0., 0.],
[1., 0., 0.],
[1., 0., 0.],
[1., 0., 0.],
[1., 0., 0.],
[1., 0., 0.],
[1., 0., 0.],
[1., 0., 0.],
[1., 0., 0.],
[1., 0., 0.],
[1., 0., 0.],
[1., 0., 0.],
[1., 0., 0.],
[1., 0., 0.],
[1., 0., 0.],
[1., 0., 0.],
[1., 0., 0.],
[1., 0., 0.],
[1., 0., 0.],
[1., 0., 0.],
[1., 0., 0.],
[1., 0., 0.],
[1., 0., 0.],
[1., 0., 0.],
[0., 1., 0.],
[0., 1., 0.],
[0., 1., 0.],
[0., 1., 0.],
[0., 1., 0.],
[0., 1., 0.],
[0., 1., 0.],
[0., 1., 0.],
[0., 1., 0.],
[0., 1., 0.],
[0., 1., 0.],
[0., 1., 0.],
[0., 1., 0.]])
torch.Size([37, 3])
# Graph connectivity in COO format with shape [2, num_edges] and type torch.long
data.edge_index
tensor([[ 0, 0, 0, 1, 1, 1, 1, 1, 2, 2, 2, 2, 2, 3, 3, 3, 3, 3,
3, 4, 4, 4, 4, 5, 5, 5, 5, 5, 6, 6, 6, 6, 7, 7, 7, 7,
7, 8, 8, 8, 9, 9, 9, 9, 9, 10, 10, 10, 10, 11, 11, 11, 11, 12,
12, 12, 12, 12, 13, 13, 13, 13, 14, 14, 14, 14, 15, 15, 15, 15, 16, 16,
16, 16, 17, 17, 17, 17, 18, 18, 18, 19, 19, 19, 20, 20, 20, 20, 20, 20,
21, 21, 21, 21, 21, 22, 22, 22, 22, 23, 23, 23, 23, 24, 24, 24, 24, 25,
25, 25, 25, 25, 26, 26, 26, 26, 26, 27, 27, 27, 27, 27, 28, 28, 28, 28,
28, 28, 29, 29, 29, 29, 29, 29, 29, 30, 30, 30, 30, 30, 31, 31, 31, 32,
32, 32, 32, 33, 33, 33, 33, 33, 33, 34, 34, 34, 34, 34, 34, 35, 35, 35,
35, 35, 36, 36, 36, 36],
[ 1, 2, 3, 0, 2, 3, 24, 27, 0, 1, 3, 27, 28, 0, 1, 2, 4, 5,
28, 3, 5, 6, 29, 3, 4, 6, 7, 29, 4, 5, 7, 8, 5, 6, 8, 9,
10, 6, 7, 9, 7, 8, 10, 11, 12, 7, 9, 11, 12, 9, 10, 12, 26, 9,
10, 11, 25, 26, 14, 15, 16, 25, 13, 15, 16, 25, 13, 14, 16, 17, 13, 14,
15, 17, 15, 16, 18, 19, 17, 19, 20, 17, 18, 20, 18, 19, 21, 22, 23, 30,
20, 22, 23, 30, 35, 20, 21, 23, 35, 20, 21, 22, 33, 1, 27, 28, 29, 12,
13, 14, 26, 29, 11, 12, 25, 28, 29, 1, 2, 24, 28, 29, 2, 3, 24, 26,
27, 29, 4, 5, 24, 25, 26, 27, 28, 20, 21, 33, 34, 35, 32, 34, 36, 31,
33, 34, 36, 23, 30, 32, 34, 35, 36, 30, 31, 32, 33, 35, 36, 21, 22, 30,
33, 34, 31, 32, 33, 34]])
# Edge feature matrix with shape [num_edges, num_edge_features]
# 这个是边的属性矩阵,类比点的属性矩阵
print(data.edge_attr)
None
# Target to train against (may have arbitrary shape),
# e.g., node-level targets of shape [num_nodes, *] or graph-level targets of shape [1, *]
print(data.y)
print(len(data.y))
tensor([5])
1
# Node position matrix with shape [num_nodes, num_dimensions]
print(data.pos)
None
None of these attributes is required. In fact, the Data object is not even restricted to these attributes. We can, e.g., extend it by data.face to save the connectivity of triangles from a 3D mesh in a tensor with shape [3, num_faces] and type torch.long.
edge,x,y = data # 得到edge,node矩阵和y即label
print(edge,x,y)
numpyx = x[1].numpy()
numpyy = y[1].numpy()
numpyedge = edge[1].numpy()
('edge_index', tensor([[ 0, 0, 0, 1, 1, 1, 1, 1, 2, 2, 2, 2, 2, 3, 3, 3, 3, 3,
3, 4, 4, 4, 4, 5, 5, 5, 5, 5, 6, 6, 6, 6, 7, 7, 7, 7,
7, 8, 8, 8, 9, 9, 9, 9, 9, 10, 10, 10, 10, 11, 11, 11, 11, 12,
12, 12, 12, 12, 13, 13, 13, 13, 14, 14, 14, 14, 15, 15, 15, 15, 16, 16,
16, 16, 17, 17, 17, 17, 18, 18, 18, 19, 19, 19, 20, 20, 20, 20, 20, 20,
21, 21, 21, 21, 21, 22, 22, 22, 22, 23, 23, 23, 23, 24, 24, 24, 24, 25,
25, 25, 25, 25, 26, 26, 26, 26, 26, 27, 27, 27, 27, 27, 28, 28, 28, 28,
28, 28, 29, 29, 29, 29, 29, 29, 29, 30, 30, 30, 30, 30, 31, 31, 31, 32,
32, 32, 32, 33, 33, 33, 33, 33, 33, 34, 34, 34, 34, 34, 34, 35, 35, 35,
35, 35, 36, 36, 36, 36],
[ 1, 2, 3, 0, 2, 3, 24, 27, 0, 1, 3, 27, 28, 0, 1, 2, 4, 5,
28, 3, 5, 6, 29, 3, 4, 6, 7, 29, 4, 5, 7, 8, 5, 6, 8, 9,
10, 6, 7, 9, 7, 8, 10, 11, 12, 7, 9, 11, 12, 9, 10, 12, 26, 9,
10, 11, 25, 26, 14, 15, 16, 25, 13, 15, 16, 25, 13, 14, 16, 17, 13, 14,
15, 17, 15, 16, 18, 19, 17, 19, 20, 17, 18, 20, 18, 19, 21, 22, 23, 30,
20, 22, 23, 30, 35, 20, 21, 23, 35, 20, 21, 22, 33, 1, 27, 28, 29, 12,
13, 14, 26, 29, 11, 12, 25, 28, 29, 1, 2, 24, 28, 29, 2, 3, 24, 26,
27, 29, 4, 5, 24, 25, 26, 27, 28, 20, 21, 33, 34, 35, 32, 34, 36, 31,
33, 34, 36, 23, 30, 32, 34, 35, 36, 30, 31, 32, 33, 35, 36, 21, 22, 30,
33, 34, 31, 32, 33, 34]])) ('x', tensor([[1., 0., 0.],
[1., 0., 0.],
[1., 0., 0.],
[1., 0., 0.],
[1., 0., 0.],
[1., 0., 0.],
[1., 0., 0.],
[1., 0., 0.],
[1., 0., 0.],
[1., 0., 0.],
[1., 0., 0.],
[1., 0., 0.],
[1., 0., 0.],
[1., 0., 0.],
[1., 0., 0.],
[1., 0., 0.],
[1., 0., 0.],
[1., 0., 0.],
[1., 0., 0.],
[1., 0., 0.],
[1., 0., 0.],
[1., 0., 0.],
[1., 0., 0.],
[1., 0., 0.],
[0., 1., 0.],
[0., 1., 0.],
[0., 1., 0.],
[0., 1., 0.],
[0., 1., 0.],
[0., 1., 0.],
[0., 1., 0.],
[0., 1., 0.],
[0., 1., 0.],
[0., 1., 0.],
[0., 1., 0.],
[0., 1., 0.],
[0., 1., 0.]])) ('y', tensor([5]))
# 将整个数据集可视化出来
g = nx.DiGraph() # 建一个空的有向图
name,edgeinfo = edge
src = edgeinfo[0].numpy()
dst = edgeinfo[1].numpy()
edgelist = zip(src,dst)
for i,j in edgelist:
g.add_edge(i,j)
plt.rcParams['figure.dpi'] = 300 #分辨率
fig , ax1 = plt.subplots(figsize=(10,10))
nx.draw_networkx(g , ax = ax1 , font_size=6 , node_size = 150)
plt.show()
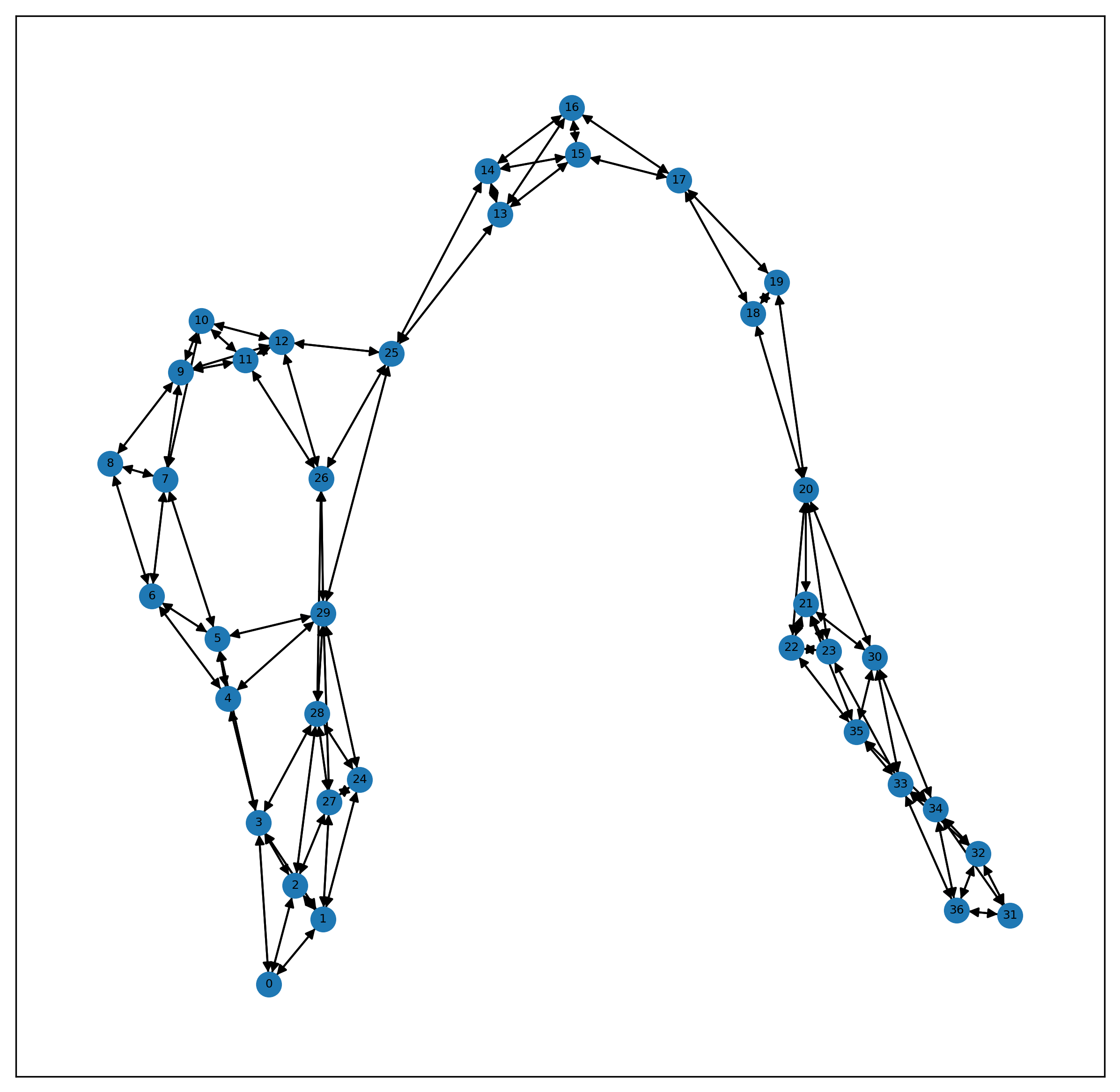
print(len(g.nodes))
g.nodes
37
NodeView((0, 1, 2, 3, 24, 27, 28, 4, 5, 6, 29, 7, 8, 9, 10, 11, 12, 26, 25, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 30, 35, 33, 34, 31, 32, 36))
2.构建GCN模型,以及训练和测试
dataset = dataset.shuffle()
train_dataset = dataset[:540]
test_dataset = dataset[540:]
len(train_dataset), len(test_dataset)
(540, 60)
class Net(torch.nn.Module):
def __init__(self):
super(Net, self).__init__()
self.conv1 = GCNConv(3, 16)
self.conv2 = GCNConv(16, 6)
def forward(self, data):
x, edge_index, batch = data.x, data.edge_index, data.batch
x = self.conv1(x, edge_index)
x = F.relu(x)
x = F.dropout(x, training=self.training)
x = self.conv2(x, edge_index)
# print(x.shape)
x = pyg_nn.global_max_pool(x, batch)
# print(x.shape)
return F.log_softmax(x, dim=1)
# 训练
def train():
model.train()
loss_all = 0
for data in train_loader:
data = data.to(device)
optimizer.zero_grad()
output = model(data)
# print(output.shape)
label = data.y.to(device)
loss = loss_f(output, label)
loss.backward()
loss_all += loss.item()
optimizer.step()
return (loss_all / len(train_dataset))
device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')
model = Net().to(device)
optimizer = torch.optim.Adam(model.parameters(), lr=0.005)
loss_f = torch.nn.CrossEntropyLoss()
train_loader = DataLoader(train_dataset, batch_size=10, shuffle=False)
for epoch in range(100):
tmp = train()
if epoch % 20 == 0:
print(tmp)
0.18143129525361237
0.1748289077370255
0.17250474073268748
0.1729406502511766
0.17272627706880922
# 测试
from sklearn.metrics import accuracy_score
def evaluate(loader):
model.eval()
with torch.no_grad():
for data in loader:
data = data.to(device)
pred = model(data).detach().numpy()
label = data.y.detach().numpy()
return pred , label
loader = DataLoader(test_dataset, batch_size=60, shuffle=False)
pred , label = evaluate(loader)
print(pred.shape , label.shape)
(60, 6) (60,)
preds = []
# list_a.index(max(list_a))
for i in range(pred.shape[0]):
tmp = pred[i].tolist()
preds.append(tmp.index(max(tmp)))
len(preds)
60
accuracy_score(label, preds)
0.2833333333333333
官网还有一种基本情况是所有数据是一张图,每个node是一个样本,然后用一些样本(node)去训练,然后预测剩余node的label,这个官网有直接的代码实现,之后也会看看。
由于我对图卷积理解尚浅,因此用的是最简单的两层图卷积,效果很差,之后再学习后可以试试搭一个复杂的GCN网络看看。
