本文作为自己学习李宏毅老师2021春机器学习课程所做笔记,记录自己身为入门阶段小白的学习理解,如果错漏、建议,还请各位博友不吝指教,感谢!!
概率生成模型
概率生成模型(Probabilistic Generative Model)简称生成模型,指一系列用于随机生成可观测数据的模型。
假设在一个连续或离散的高维空间 X \mathcal{X} X中,存在一个随机向量 X \mathnormal{X} X服从一个未知的数据分布 p r ( x ) , x ∈ X p_r(x), x \in \mathcal{X} pr?(x),x∈X。生成模型根据一些可观测的样本 x ( 1 ) , x ( 2 ) , ? ? , x ( N ) x^{(1)},x^{(2)}, \cdots ,x^{(N)} x(1),x(2),?,x(N)来学习一个参数化的模型 p θ ( x ) p_\theta(x) pθ?(x)来近似未知分布 p r ( x ) p_r(x) pr?(x),并可以用这个模型来生成一些样本,使得生成的样本和真实的样本尽可能地相似。
生成模型的两个基本功能:概率密度估计和生成样本(即采样)。
隐式密度模型
在生成模型的生成样本功能中,如果只是希望一个模型能生成符合数据分布 p r ( x ) p_r(x) pr?(x)的样本,可以不显示的估计出数据分布的密度函数。
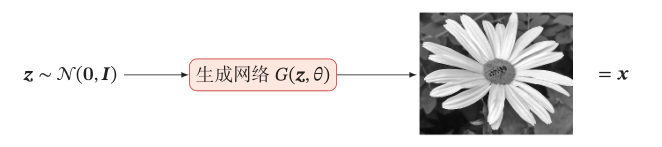
假设在低维空间 Z \mathcal{Z} Z中有一个简单容易采样的分布 p ( z ) p(z) p(z), p ( z ) p(z) p(z)通常为标准多元正态分布 N ( 0 , I ) \mathcal{N}(0,\mathnormal{I}) N(0,I),我们用神经网络构建一个映射函数 G : Z → X G : \mathcal{Z} \rightarrow \mathcal{X} G:Z→X,称为生成网络。利用神经网络强大的拟合能力,使得 G ( z ) G(z) G(z)服从数据分布 p r ( x ) p_r(x) pr?(x)。这种模型就称为隐式密度模型(Implicit Density Model)。
隐式密度模型生成样本的过程如下图所示:
生成对抗网络
生成对抗网络(Generative Adversarial Networks,GAN)是一种隐式密度模型,包括判别网络(Discriminator Network)和生成网络(Generator Network)两个部分,通过对抗训练的方式来使得生成网络产生的样本服从真实数据分布。
在生成对抗网络中:
- 判别网络:目标是尽量准确地判断一个样本是来自于真实数据还是由生成网络产生。
- 生成网络:目标是尽量生成判别网络无法区分来源的样本。
生成对抗网络的训练过程
在训练过程中,将判别网络和生成网络两个网络不断地进行交替训练。当最后收敛时,如果判别网络再也无法判断一个样本地来源,那么也就等价于生成网络可以生成符合真实数据分布的样本。生成对抗网络的流程图如下图所示:

以李宏毅老师所举的生成二次元头像的例子来看生成对抗网络的训练过程:
Step 1:固定生成网络,训练判别网络
在完成生成网络和判别网络参数的初始化之后,固定住生成网络,我们将从分布 p ( z ) p(z) p(z)中采样出来的向量输入到生成网络中,得到对应的输出(图片)。
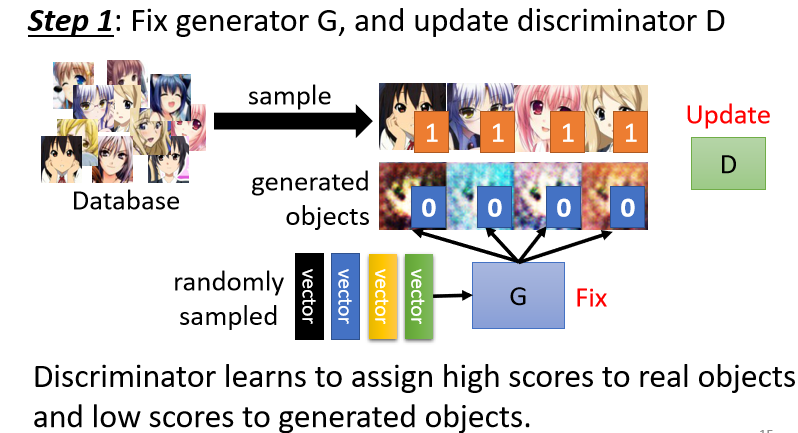
我们拿得到的输出结果与真正的二次元头像来训练判别网络,目标是让判别网络学习这两中图片之间的差异,从而可以将他们进行区分。具体来说,我们可以将真正的二次元头像图片标为1,生成网络的输出结果标为0。接下来,我们既可以将此看作一个分类问题,也可以看作一个回归问题:
- 分类问题:将真正的头像看作类别1,生成网络产生的图像看作类别2,然后利用这些图片训练一个分类器。
- 回归问题:训练判别网络看到真正的头像图片时输出1,看到生成网络生成的头像图片时输出0,来学习两者之间的差异。
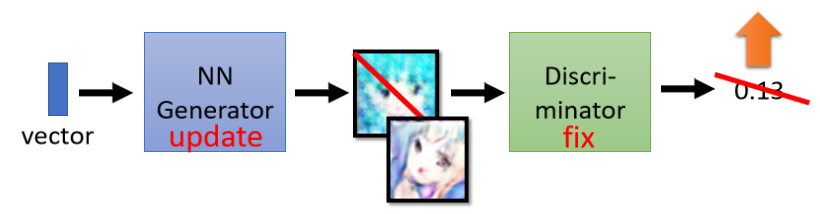
Step 2: 固定判别网络,训练生成网络
我们将生成网络输出的图片输入到判别网络中,最终训练的目标是是让判别网络的输出值越大越好。判别网络在训练的过程中就是看到好的图片就给它大的分数,如果生成网络调整参数后输出的图片在判别网络中得到高分,那意味着生成网络生成的图片是比较真实的。
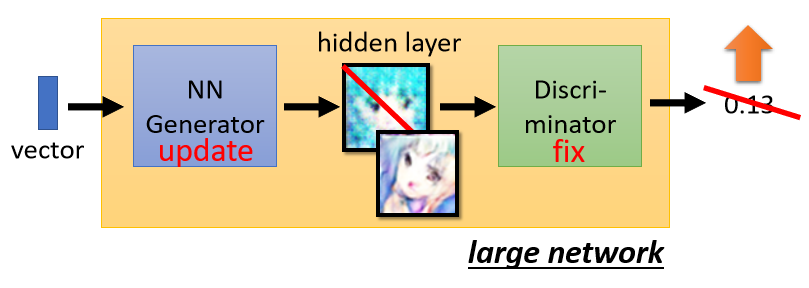
在这个训练过程中,可以看作将Generator和Discriminator拼接成一个更大的网络,在这个更大的网络中,我们固定住属于Discriminator的隐藏层的参数,只更新属于Generator的隐藏层的参数。Generator和Discriminator拼接的中间部分有一个很宽的中间层,在该层中,我们将Generator输出的结果整理成图片的形式输入到Discriminator中得到分类得分。
生成网络
我们在训练一个网络的时候,基本的思路是:
- 确定一个Loss Function
- 使用Gradient Descent 调节参数
- 然后最小化Loss Function就可以了
那在生成网络中,我们要Minimize或者Maximize的目标是什么呢?在该网络中,我们首先输入从Normal Distribution 中采样出来的向量,得到一个比较复杂的分布
p
θ
(
x
)
p_\theta(x)
pθ?(x),而真实的数据形成另一个分布
p
r
(
x
)
p_r(x)
pr?(x)。那么在生成网络中,我们的目标就是让
p
θ
(
x
)
p_\theta(x)
pθ?(x)和
p
r
(
x
)
p_r(x)
pr?(x)越接近越好,表达为如下公式:
G
?
=
a
r
g
min
?
G
D
i
v
(
p
θ
,
p
r
)
(1)
G^*=arg\min_{G}Div(p_\theta, p_r) \tag{1}
G?=argGmin?Div(pθ?,pr?)(1)
其中
D
i
v
Div
Div表示
p
θ
(
x
)
p_\theta(x)
pθ?(x)和
p
r
(
x
)
p_r(x)
pr?(x)两个分布之间的散度(Divergence)。散度是衡量两个分布之间相似度的标准,散度越大,表示两个分布越不像,散度越小,表示两个分布越像。但是,这个作用在连续的分布上的散度,我们是无法计算出来的,那突破这一计算限制的方法就是和判别网络交替训练完成优化。
判别网络
如果看作一个分类问题,在判别网络中,给定一个样本
(
x
,
y
)
(x,y)
(x,y),
y
=
{
1
,
0
}
y=\{1,0\}
y={1,0}表示样本来自真实分布
p
r
(
x
)
p_r(x)
pr?(x)还是生成模型
p
θ
(
x
)
p_\theta(x)
pθ?(x),则判别网络
D
(
x
;
?
)
D(x;\phi)
D(x;?)的输出为样本
x
x
x属于真实数据分布的概率:
p
(
y
=
1
∣
x
)
=
D
(
x
;
?
)
(2)
p(y=1|x)=D(x;\phi) \tag{2}
p(y=1∣x)=D(x;?)(2)
那样本来自生成模型的概率为:
p
(
y
=
0
∣
x
)
=
1
?
D
(
x
;
?
)
(3)
p(y=0|x)=1 - D(x;\phi) \tag{3}
p(y=0∣x)=1?D(x;?)(3)
所以,判别网络的目标函数为最小化交叉熵,即:
min
?
?
?
(
E
x
[
y
l
o
g
p
(
y
=
1
∣
x
)
+
(
1
?
y
)
l
o
g
p
(
y
=
0
∣
x
)
]
)
(4)
\min_{\phi}- (\mathbb{E}_x[ylog p(y=1|x)+(1-y)logp(y=0|x)]) \tag{4}
?min??(Ex?[ylogp(y=1∣x)+(1?y)logp(y=0∣x)])(4)
假设分布
p
(
x
)
p(x)
p(x)是由分布
p
r
(
x
)
p_r(x)
pr?(x)和分布
p
θ
(
x
)
p_\theta(x)
pθ?(x)等比例混合而成,即
p
(
x
)
=
1
2
(
p
r
(
x
)
+
p
θ
(
x
)
)
p(x)=\frac{1}{2}(p_r(x)+p_\theta(x))
p(x)=21?(pr?(x)+pθ?(x)),则上式等价于:
max
?
?
V
(
D
,
G
)
=
max
?
?
E
x
~
p
r
(
x
)
[
l
o
g
D
(
x
;
?
)
]
+
E
x
′
~
p
θ
(
x
′
)
[
l
o
g
(
1
?
D
(
x
′
;
?
)
)
]
=
max
?
?
E
x
~
p
r
(
x
)
[
l
o
g
D
(
x
;
?
)
]
+
E
z
~
p
(
z
)
[
l
o
g
(
1
?
D
(
G
(
z
;
θ
)
;
?
)
)
]
(5)
\begin{aligned} &\max_\phi V(D,G) \\ =&\max_{\phi} \mathbb{E}_{x \sim p_r(x)}[logD(x;\phi)]+\mathbb{E}_{x' \sim p_\theta(x')}[log(1-D(x';\phi))] \\ =& \max_{\phi}\mathbb{E_{x \sim p_r(x)}}[logD(x;\phi)] + \mathbb{E}_{z \sim p(z)}[log(1-D(G(z;\theta); \phi))] \end{aligned} \tag{5}
==??max?V(D,G)?max?Ex~pr?(x)?[logD(x;?)]+Ex′~pθ?(x′)?[log(1?D(x′;?))]?max?Ex~pr?(x)?[logD(x;?)]+Ez~p(z)?[log(1?D(G(z;θ);?))]?(5)
- E x ~ p r ( x ) \mathbb{E}_{x \sim p_r(x)} Ex~pr?(x)?:是将真实的图像数据输入到判别网络中,得到一个分数再取 l o g D ( x ; ? ) logD(x;\phi) logD(x;?),为了让公式(5)中的目标函数越大,该项的值越大越好。
- E z ~ p ( z ) \mathbb{E}_{z \sim p(z)} Ez~p(z)?:是将生成的图像数据输入到判别网络中,得到一个分数再取 l o g ( 1 ? D ( G ( z ; θ ) ; ? ) ) log(1-D(G(z;\theta); \phi)) log(1?D(G(z;θ);?)),为了让公式(5)中的目标函数越大,该项的值越小越好。
而根据GAN原始的Paper,这里的公式(5)得到的结果和公式(1)中的散度其实是相关的。如下图所示:
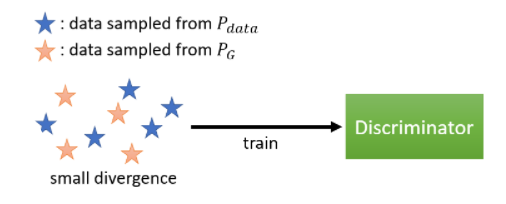
图中 P d a t a P_{data} Pdata?表示真实分布, P G P_G PG?表示生成器产生的分布。在该图中,直观的来说,两个分布的散度比较小,代表真实图像的蓝色星星和代表生成图像的红色星星混合在一起,我们使用判别网络很难将其分开,所以我们在解这个优化问题的时候,就没有办法让这个目标函数的值非常的大,最终得到的公式(5)的值就比较小。
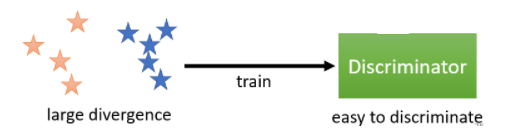
在该图中,两组数据很不像,他们的散度很大,而且我们使用判别网络可以轻易的将他们分开,此时的目标函数的值也就变的很大。综上所述,小的公式(5)的值对应小的散度,大的公式(5)的值对应大的散度。
既然公式(5)中的目标函数和衡量分布差异的散度相关,不妨做如下替换:
G
?
=
a
r
g
min
?
G
max
?
D
V
(
G
,
D
)
(6)
G^* = arg \min_{G}\max_{D}V(G,D) \tag{6}
G?=argGmin?Dmax?V(G,D)(6)
这个就是生成网络所要解的目标函数了,而求解过程则是生成网络和判别网络交替训练完成的。
参考资料:
《神经网络与深度学习》 邱锡鹏