[人工智能]2021-07-14 深度学习基础与实践（二）

一、分类及其性能度量

1.分类问题

• 分类问题是有监督学习的一个核心问题。分类解决的是要预测样本属于哪个或者哪些预定义的类别。此时输出变量通常取有限个离散值。

• 分类的机器学习的两大阶段：
  1）从训练数据中学习得到一个分类决策函数或分类模型，称为分类器(classifier)；
  2）利用学习得到的分类器对新的输入样本进行类别预测；

• 两类分类问题与多类分类问题
  1）两类分类问题：将标记分为两类
  2）多类分类问题：将标记分为多类
  多类分类问题也可以转化为两类分类问题解决，如采用一对其余(One-vs-Rest)的方法：将其中一个类标记为正类，然后将剩余的其它类都标记成负类。
  

2.分类性能度量

在解决了一个分类问题之后，对这一次分类的结果进行评判度量显然是不可或缺的，因为一次分类的过程中可能难免会产生一些错误，所以每一次的分类都应该有所谓相对的“较好的分类”和“较不好的分类之分”，那么我们可以从哪几个方面去对它的分类性能进行度量和评估呢？
可以尝试从以下几个方面去考虑：

(1)准确率

• 假设只有两类样本，即正例(positive)和负例(negative)。通常以关注的类为正类，其他类为负类。

• 分类准确率(accuracy)：分类器正确分类的样本数与总样本数之比：$$accuracy=\frac{TP+TN}{P+N}$$

(2)精确率和召回率

我们试着来思考一个问题：
既然前面已经给出准确率(accuracy)的度量指标了，准确率不是已经可以评判分类完成的好坏了吗，那为什么我们还要继续推出和介绍更多的度量指标呢？

其实准确率确实可以在一定程度上度量分类完成的好坏，但它在一定程度上过于片面，有所局限。我们来看一个通俗易懂的例子：

假设我们现在在一个池塘里打鱼，我们打了两次鱼，第一次渔网里仅仅包括了池塘里所有的鱼，第二次渔网里不仅包括了池塘里的所有鱼，还打捞上了许多水草和杂物。那么我们试着去评判以下这两次捕捞哪一次是更好的，虽然两次捕捞都实现了捞上所有鱼的目标，但答案显然是第一次的捕捞效果更好。所以一方面的评判标准（准确率）往往是不够的，我们需要从多个角度来度量。

• 精确率(precision)和召回率(recall)：是二类分类问题常用的评价指标。$$precision=\frac{TP}{TP+FP}$$ $$recall=\frac{TP}{P}$$

• 精确率反映了模型判定的正例中真正正例的比重。在垃圾短信分类器中，是指预测出的垃圾短信中真正垃圾短信的比例。

• 召回率反映了总正例中被模型正确判定正例的比重。医学领域也叫做灵敏度（sensitivity）。在垃圾短信分类器中，指所有真的垃圾短信被分类器正确找出来的比例。

(3)P-R曲线

• Area (Area Under Curve, 或者简称AUC)

• Area的定义（p-r曲线下的面积）如下: $$Area={\int }_0^{1}p(r)dr$$

• Area有助于弥补P、R的单点值局限性，可以反映全局性能（往往难以同时保证precision和recall都在一个比较高的水准）

• P-R曲线的绘制
  要得到P‐R曲线，需要一系列precision和recall的值。这些系列值是通过设定阈值来形成的。
  
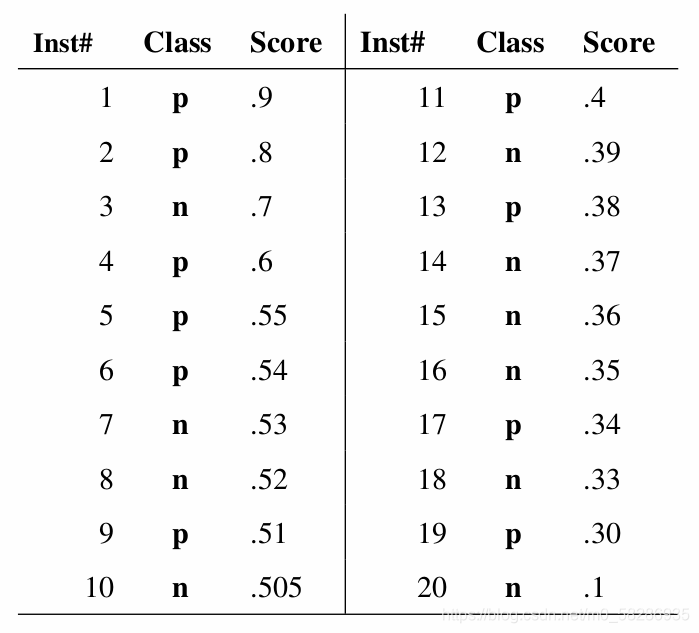
  例如上图中有20个样本，Inst#代表样本序号，Class代表ground truth真值标签，p代表该样本是positive（正例），n代表该样本是negative（负例），Score是我的分类器对于该样本属于正例的可能性的打分（概率值）。

  然后从高到低将Score值排序并依此作为阈值threshold，Score大于等于阈值的样本被标注为正例，Score小于阈值的样本被标注为负例。

  显然，如果我设置n个阈值，我就能得到n种标注结果，来评判我的模型好不好使。

  • 若阈值设置为0.9，只有第一个样本被我判断为正例，那么我的精确率$precision=\frac{TP}{TP+FP}=100\%$，但是召回率$recall=\frac{TP}{P}=10\%$。
    …
  • 若阈值设置为0.1，所有样本都被我判断为正例，精确率$precision=\frac{TP}{TP+FP}=50\%$，召回率$recall=\frac{TP}{P}=100\%$。

  最后就能得到若干对$precision$和$recall$值的二元组$(P,R):(1,0.1),...,(0.5,1)$，将这若干二元组看作坐标画在图上，再连接起来就是这个模型对应的P-R曲线了。

(4)F值

• F值$(F_{\beta }?score)$是精确率和召回率的调和平均: $$F_{\beta }?score=\frac{(1+{\beta }^2)?precision?recall}{{\beta }^2?precision+recall}$$

• $\beta$一般大于0。当 $\beta =1$ 时，退化为F1：$$F_1?score=\frac{2?precision?recall}{precision+recall}$$

• 比较常用的是F1 , 即表示precision和recall二者同等重要。

(5)ROC曲线

• 横轴：假正例率 $fprate=\frac{FP}{N}$

• 纵轴：真正例率 $tprate=\frac{TP}{P}$

• ROC (受试者工作特征曲线, receiver operating characteristic curve)描绘了分类器在$tprate$(真正正例占总正例的比率，反映命中概率，纵轴)和$fprate$ (错误的正例占反例的比率，反映误诊率、假阳性率、虚惊概率，横轴) 间的trade‐off。

• ROC曲线的绘制
  要得到一个曲线，需要一系列$fprate$和$tprate$的值。这些系列值是通过设定阈值来形成的。
  
  同样，还是以上面那张表格为例。

  然后从高到低将Score值排序并依此作为阈值threshold，Score大于等于阈值的样本被标注为正例，Score小于阈值的样本被标注为负例。

  显然，如果我设置n个阈值，我就能得到n种标注结果。

  • 若阈值设置为0.9，只有第一个样本被我判断为正例，那么真正例率（纵轴）$tprate=\frac{TP}{P}=10\%$，假正例率（横轴）$fprate=\frac{FP}{N}=0\%$。
    …
  • 若阈值设置为0.1，所有样本都被我判断为正例，那么真正例率（纵轴）$tprate=\frac{TP}{P}=100\%$，假正例率（横轴）$fprate=\frac{FP}{N}=100\%$。

  最后就能得到若干对$fprate$和$tprate$的二元组$(T,F):(0.1,0),...,(1,1)$，将这若干二元组看作坐标画在图上，再连接起来就是这个模型对应的ROC曲线了。

• ROC‐AUC计算
  ROC‐AUC（Area Under Curve）定义为ROC曲线下的面积。
  AUC值提供了分类器的一个整体数值。
  通常AUC越大，分类器更好。取值范围为[0,1]。

3.分类性能可视化

(1)混淆矩阵的可视化

• 如用热图（heatmap）直观地展现类别的混淆情况（每个类有多少样本被错误地预测成另一个类）
  

(2)分类报告

• 显示每个类的分类性能。包括每个类标签的精确率、召回率、F1值等。
  

二、回归问题及其性能评价

1.什么是回归

• 回归分析（regression analysis)是确定两种或两种以上变量间相互依赖的定量关系的一种统计分析方法。

• 和分类问题不同，回归通常输出为一个实数数值。而分类的输出通常为若干指定的类别标签。

2.回归性能度量方法

(1)平均绝对误差MAE

• MAE(Mean absolute error)是绝对误差损失(absolute error loss)的期望值。

• 如果${\hat{y}}_i$是第i个样本的预测值，$y_i$是相应的真实值，那么在$n_{samples}$个测试样本上的平均绝对误差（MAE）的定义如下：$$MAE(y,\hat{y})=\frac{1}{n_{samples}}\sum _{i=0}^{n_{samples}?1}|y_i?{\hat{y}}_i|$$

(2)均方差MSE

• MSE(Mean squared error)，该指标对应于平方误差损失 (squared error loss)的期望值。

• 如果${\hat{y}}_i$是第i个样本的预测值，$y_i$是相应的真实值，那么在$n_{samples}$个测试样本上的均方差的定义如下：$$MSE(y,\hat{y})=\frac{1}{n_{samples}}\sum _{i=0}^{n_{samples}?1}|y_i?{\hat{y}}_i{|}^2$$

• 均方根差RMSE: Root Mean Squared Error, RMSE,是MSE的平方根。

• 均方差MSE的应用举例
  

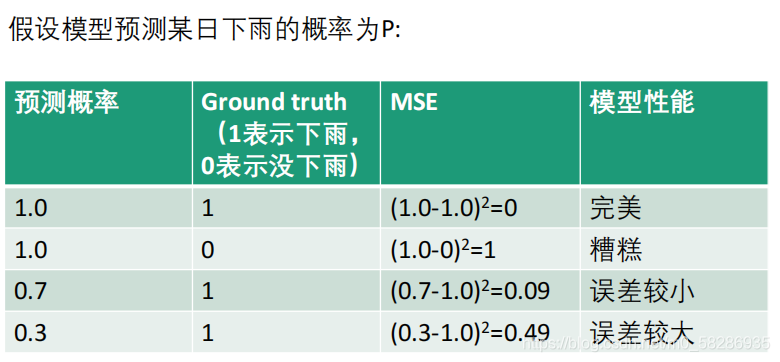
(3)logistic回归损失(二类)

• 简称Log loss，或交叉熵损失(cross‐entropy loss)
  常用于评价逻辑回归LR和神经网络

• 对于二类分类问题

  1. 假设某样本的真实标签为y(取值为0或1)，概率估计为$p=P(y=1)$
  2. 每个样本的log loss是对分类器给定真实标签的负log似然估计(negative log‐likelihood)：$$L_{log}(y,p)=?log(P(y|p))=?(ylog(p)+(1?y)log(1?p))$$

• 公式：$$L_{log}(y,p)=?log(P(y|p))=?(ylog(p)+(1?y)log(1?p))$$

(4)logistic回归损失(多类)

• 对于多类问题(multiclass problem)，可将样本的真实标签(true label)编码成1‐of‐K（K为类别总数）的二元指示矩阵Y。

• 举例：假设有三类

• 假设模型对测试样本的概率估计结果为P，则在测试集(假设测试样本总数为N)上的交叉熵损失表示如下：$$L_{log}(y,p)=?log(P(y|p))=?\frac{1}{N}\sum _{i=0}^{N?1}\sum _{k=0}^{K?1}{y}_{i,k}log{p}_{i,k}$$
  其中$y_{i,k}$表示第i个样本的第k个标签的真实值，注意由于表示为“1‐of‐K”模式，因此每个样本只有其中一个标签值为1，其余均为0。$p_{i,k}$表示模型对该样本的预测值。

• 举例：6个样本，三个类
  

三、一致性的评价方法

• 一致性评价
  一致性评价，是指对两个或多个相关的变量进行分析，从而衡量其相关性的密切程度。

• 假设一个场景：有两位评委要对5部电影进行评分，评分区间为[0,5]，结果如下：
  rater1 = [0.5, 1.6, 2.5, 2.5, 2.4]
  rater2 = [1.5, 2.6, 3.5, 3.5, 3.4]
  那么请问两者意见的一致性如何？

  下面介绍几种一致性的评价方法

1.皮尔森相关系数法

• 皮尔森相关系数(Pearson coefficient)的应用背景：
  用来衡量两个用户之间兴趣的一致性
  用来衡量预测值与真实值之间的相关性
  既适用于离散的、也适用于连续变量的相关分析

• X和Y之间的皮尔森相关系数计算公式：$${\rho }_{X,Y}=\frac{cov(X,Y)}{{\sigma }_X{\sigma }_Y}=\frac{E[(X?{\mu }_X)(Y?{\mu }_Y)]}{{\sigma }_X{\sigma }_Y}$$
  其中，$cov(X,Y)$表示X和Y之间的协方差（Covariance），$\sigma$是均方差，$\mu$是均值, $E$表示数学期望

• 取值区间为[‐1,1]。‐1:完全的负相关；+1:表示完全的正相关；0:没有线性相关

2.Cohen’s kappa相关系数

• Cohen‘s kappa相关系数也可用于衡量两个评价者之间的一致性。其特点在于：
  1. 与pearson相关系数的区别：Cohen‘s kappa相关系数通常用于离散的分类的一致性评价。
  2. 其通常被认为比两人之间的简单一致百分比更强壮，因为Cohen‘s kappa考虑到了二人之间的随机一致的可能性。
• 如果评价者多于2人时，可以考虑使用Fleiss’ kappa。
  （Cohen’s kappa与Fleiss’ kappa的计算方法不做过多介绍，感兴趣的朋友可以去自行了解）