01 应用

举例	English	输入	输出	思考
股票预测	stock market forecast	股票市场，新闻资讯（xx并购xx这种）	明天的道琼指数	非常nice，新闻资讯用nlp
自动驾驶	self-driving car	马路信息	方向盘角度	输出还应包含速度之类的
推荐系统	recommendation	使用者A，商品B	购买可能性	用户画像？商品也应该是多维度的数据，结构化输入？

当然，还有更实用的，预测宝可梦进化后的CP值（战斗力）！
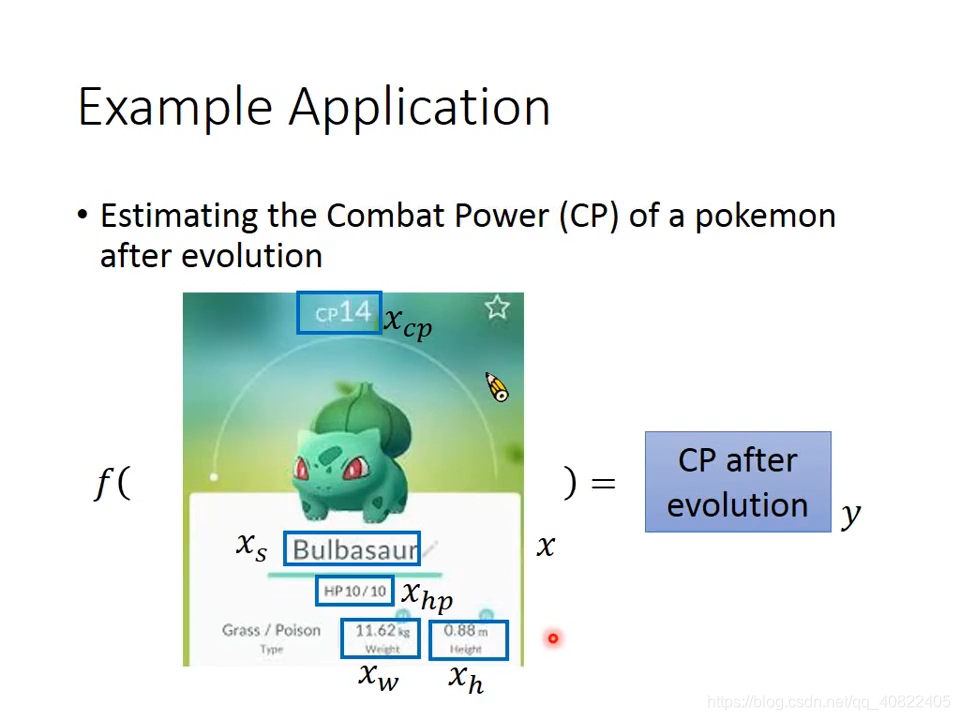
在这里插入图片描述
按照上一讲给出的机器学习流程，无非就是三个步骤，函数集，Goodness（适应度？），选出最好的函数。

02 Design Function

首先考虑只有一个变量的，进化前的CP值，以最简单的线性函数作为函数集。
在这里插入图片描述
将w称为权重（weight），b称为偏置（bias），输入的x称为特征（feature），下标i代表函数里的内容（区别于接下来的上标i代表样本i）。
在这个函数集里，如果w和b确定后，就能唯一确定一个函数，先不管是否最优，总是能根据进化前的CP值x输出进化后的CP值y。
这样一来，下一个问题，如何确定这个函数是不是最优的？一个可行的方法是衡量这个函数输出与真实值的差距。

03 Loss Function

机器学习里还有目标函数（goal function）和代价函数（cost function），它们的目的都是一样的，衡量函数输出与真实值的差距。
在这里插入图片描述
在这里用了简单的方差来衡量，为什么这么做，涉及到数学推导，不过马上就会看到一个好处。
将所有样本的真实值与函数输出的预测值的方差求和作为损失，损失越小说明效果越好。于是现在问题变成了，怎么让损失值变小？
很显然，这是w和b的函数，可以通过改变w和b来使损失变小。又回到了原点？
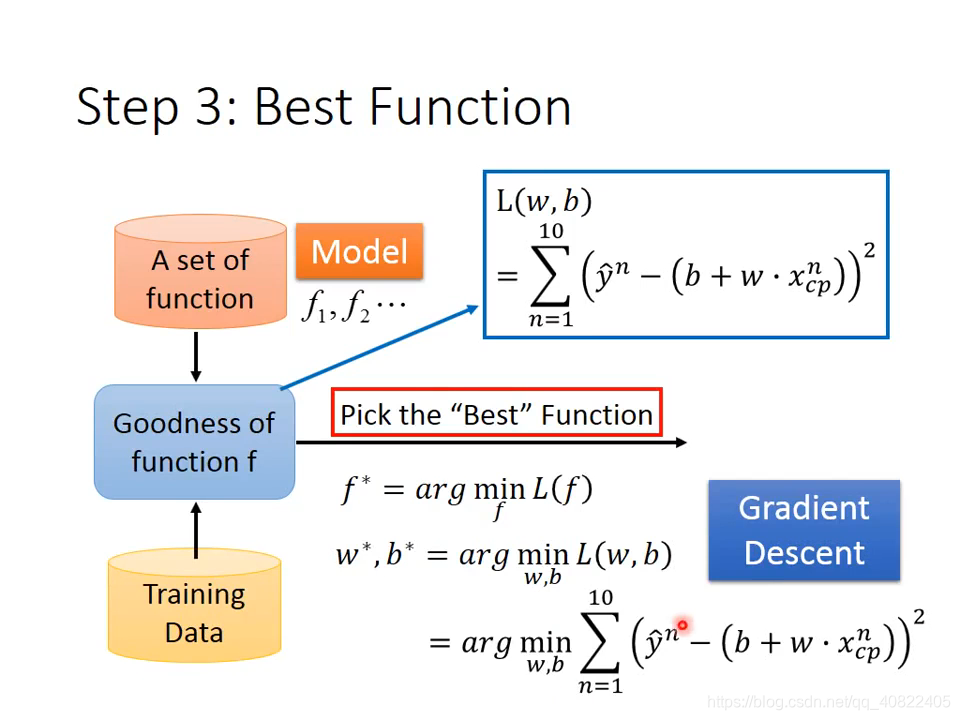
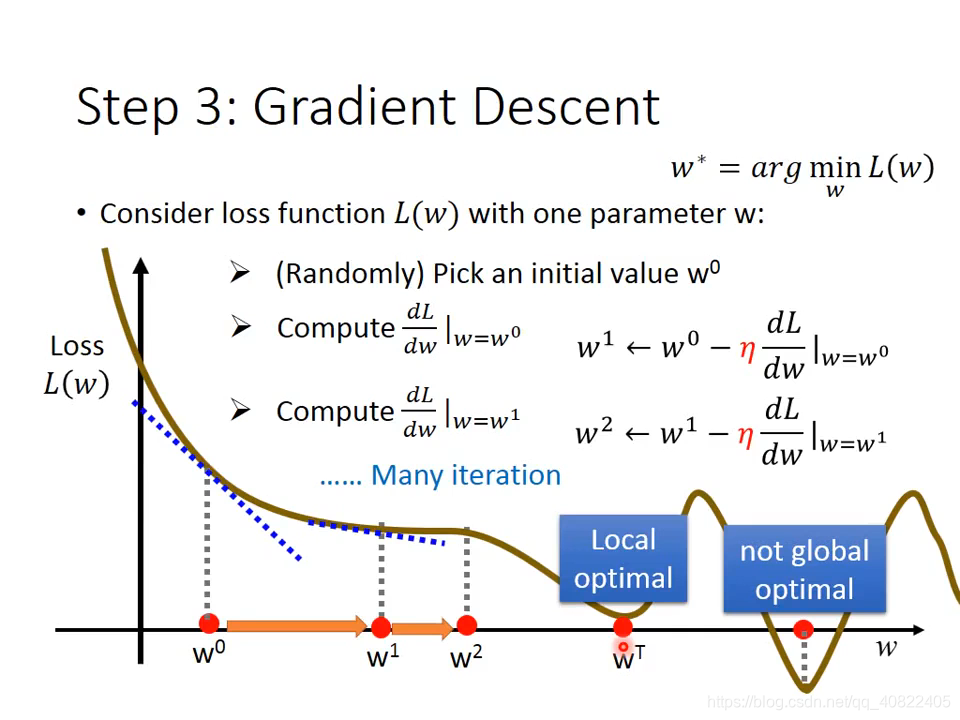
在这里插入图片描述