从之前的学习中，可以知道，回归 Regression 和 分类 Classification 是非常重要的两个概念
那么回归是什么呢？
Regression 就是找到一个函数 function ，通过输入特征 xx，输出一个数值 Scalar。
它的结果是一个数值；同时某种程度上它也是一种预测；
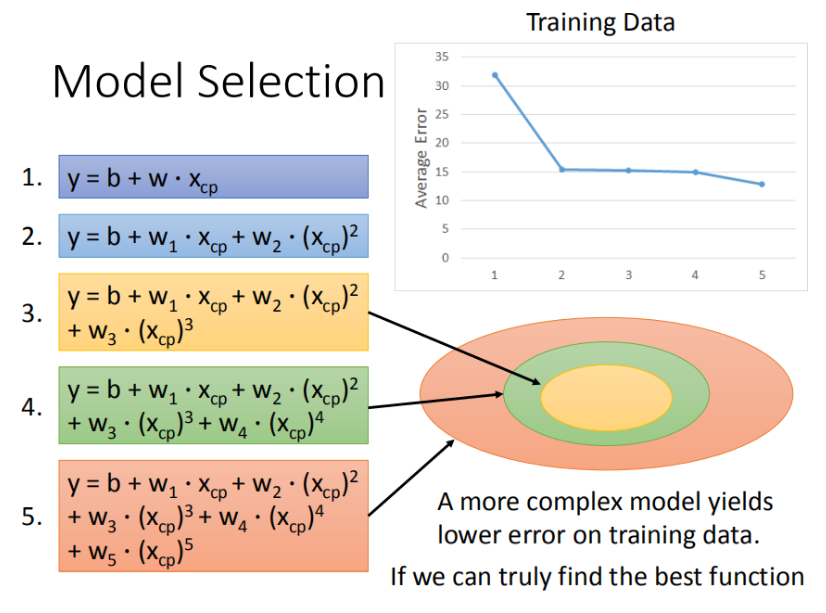
模型步骤
step1：模型假设，选择模型框架（线性模型）
可以类比为感知机吧，这里？
y = b + w ? x c p y = b + w·x_{cp} y=b+w?xcp? ； ω \omega ω为权重，b可以看作为结果值，
y=0 则为决策边界
抽象为多个特征（权重向量和特征向量）
w = ( w 1 w 2 ? w n ) , x = ( x 1 x 2 ? x n ) \boldsymbol{w}=\begin{pmatrix}w_1\\w_2\\\vdots\\w_n\end{pmatrix},\quad\boldsymbol{x}=\begin{pmatrix}x_1\\x_2\\\vdots\\x_n\end{pmatrix} w=??????w1?w2??wn????????,x=??????x1?x2??xn????????
那么可通过点积可得：
d ( x 1 , x 2 , ? ? , x n ) = w 1 x 1 + w 2 x 2 + ? + w n x n + b = w ? x + b \begin{aligned}d(x_1,x_2,\cdots,x_n)&=w_1x_1+w_2x_2+\cdots+w_nx_n+b\\&=\boldsymbol{w}\cdot\boldsymbol{x}+b\end{aligned} d(x1?,x2?,?,xn?)?=w1?x1?+w2?x2?+?+wn?xn?+b=w?x+b?
y = d ( x ) = w ? x + b y=d(\boldsymbol{x})=\boldsymbol{w}\cdot\boldsymbol{x}+b y=d(x)=w?x+b 将b看成偏移量。
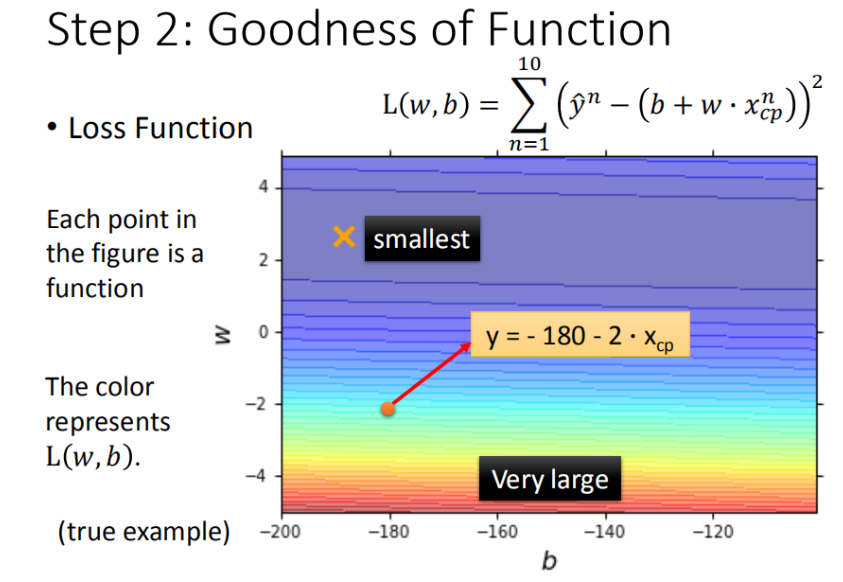
step2：模型评估，如何判断众多模型的好坏（损失函数）
loss function ：方差
x n x^n xn 是材料， y n = f ( x n ) y^n=f(x^n) yn=f(xn)是计算的结果， y ^ n \hat{y}^n y^?n是真正的结果，（ y ^ n \hat{y}^n y^?n所代表的是真实值）
L ( f ) = n = 1 ∑ 10 ( y n ? f ( x c p n ) ) 2 L(f)=n=1∑10(y^n?f(xcpn))2 L(f)=n=1∑10(yn?f(xcpn))2，将【 f ( x ) = y f(x)=y f(x)=y】,【 y = b + w ? x c p y=b+w?xcp y=b+w?xcp】代入 = ∑ 10 ( y n ? ( b + w ? x c p ) ) 2 =∑10(y^n?(b+w?xcp))2 =∑10(yn?(b+w?xcp))2$
]
最终定义 损失函数 Loss function： L ( w , b ) = ∑ n = 1 10 ( y ^ n ? ( b + w ? x c p ) ) 2 L(w,b)= \sum_{n=1}^{10}\left ( \hat{y}^n - (b + w·x_{cp}) \right )^2 L(w,b)=n=1∑10?(y^?n?(b+w?xcp?))2
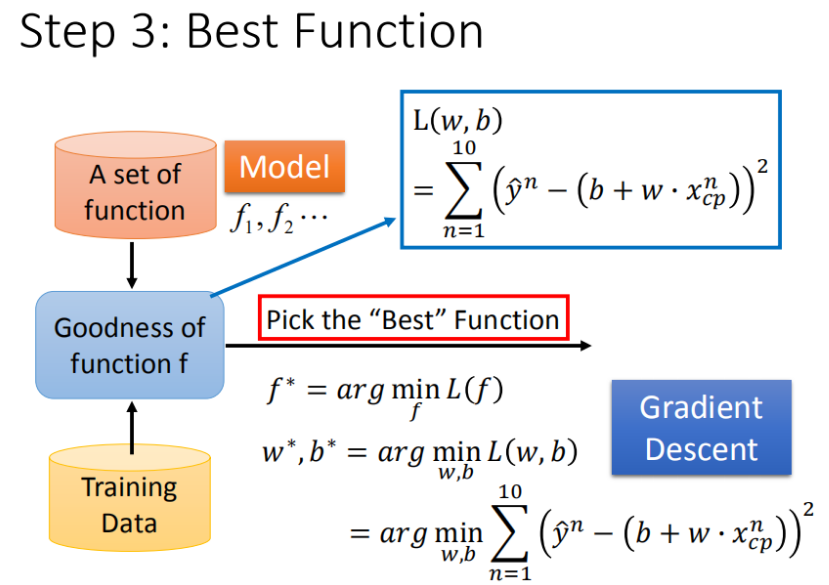
step3：模型优化，如何筛选最优的模型（梯度下降）
]
通过求极限斜率
!筛选最优的模型（参数w，b）
理想化当前场景为单个特征：已知损失函数是 L ( w , b ) = ∑ n = 1 10 ( y ^ n ? ( b + w ? x c p ) ) 2 L(w,b)= \sum_{n=1}^{10}\left ( \hat{y}^n - (b + w·x_{cp}) \right )^2 L(w,b)=∑n=110?(y^?n?(b+w?xcp?))2，需要找到一个令结果最小的 f ? f^* f?，在实际的场景中，我们遇到的参数肯定不止 w , b w, b w,b
先计算权重
ω
\omega
ω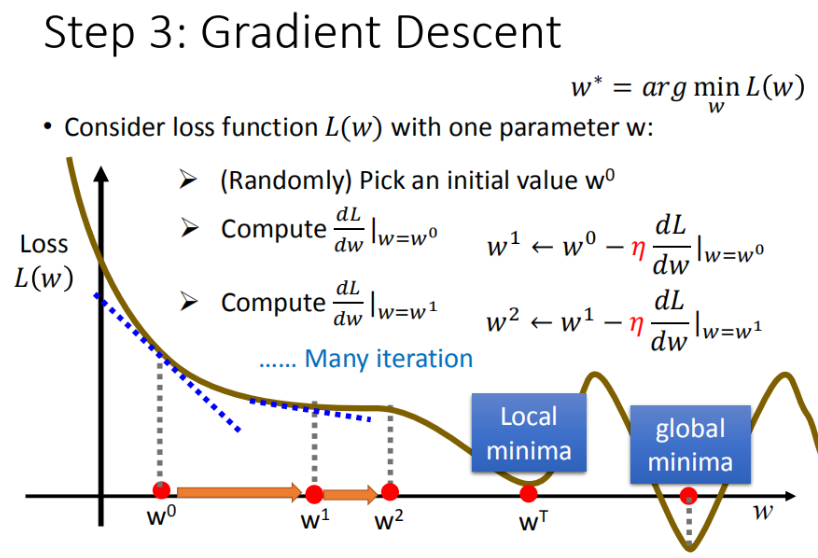
验证训练好的模型的好坏
训练集和测试集的平均误差来验证模型的好坏
线性系统模型：1元N次
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传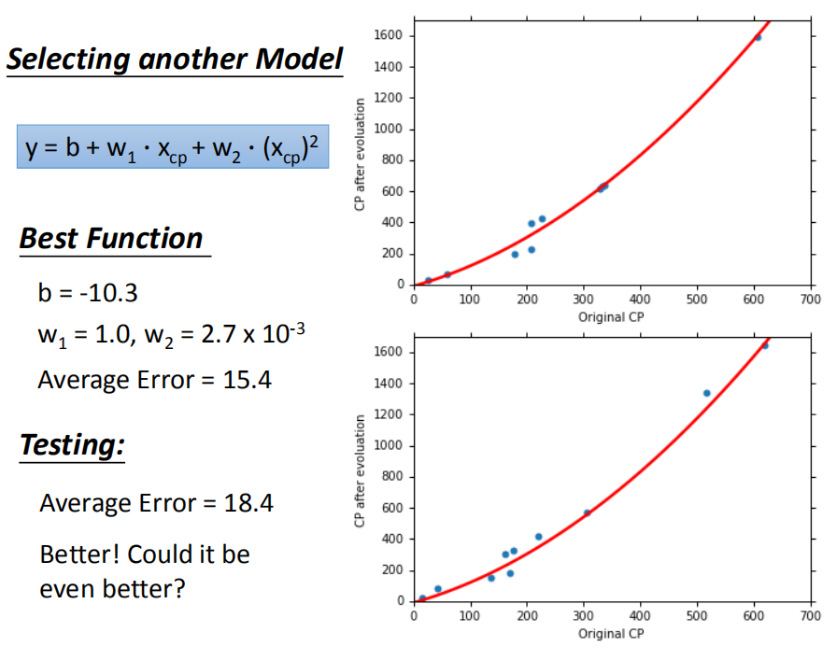
]训练集求得平均误差为15.4，测试集的平均误差为18.4
过拟合问题出现
本来在某些训练集非常符合的，却在某些情况下的测试结果变差了，和不可预测。
