[人工智能]改善深层神经网络：超参数调试、正则化以及优化(Improving Deep Neural Networks:Hyperparameter tuning Regularizatio)

1.1 训练、开发、测试集

train set训练集 Dev set验证集 test set 测试集

小规模数据：训练集：其他 = 7:3

大数据时代（超百万数据）：训练集占80%或者90%以上

验证集和测试集来自同一分布

如果只有训练集和验证集，那么验证集Dev set就是测试集test set

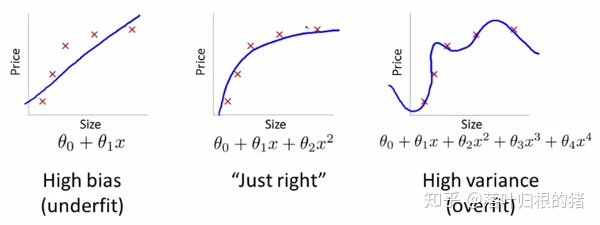
1.2 偏差、方差

1.3 机器学习基础

high bias(train data problem) ——big network

high variance(dev set problem)——more data/regularization

1.4 正则化

$$\begin{gathered} mi{n}_{w,b}J(w,b) \\ J(w,b)=\frac{1}{m}\sum _{i=1}^{m}L({\hat{y}}^{(i)},y^{(i)})+\frac{\lambda }{2m}||w|{|}^2+\frac{\lambda }{2m}{b}^2(omit) \\ L2regularization:||w|{|}^2=\sum _{j=1}^{nx}{w}_j^2=w^{T}w \\ L1regularization:\frac{\lambda }{2m}\sum _{j=1}^{nx}|w_j|=\frac{\lambda }{2m}\sum _{j=1}^{nx}||w|{|}_1 \end{gathered}$$

$$\begin{gathered} J(w^{[1]},b^{[1]},\dots \dots w^{[l]},b^{[l]})=\frac{1}{m}\sum _{i=1}^{m}L({\hat{y}}^{(i)},y^{(i)})+\frac{\lambda }{2m}||w^{[l]}|{|}_F^2 \\ \frac{\lambda }{2m}||w^{[l]}|{|}_F^2=\sum _{i=1}^{n^{[l?1]}}\sum _{j=1}^{n^{[l]}}(w_{ij}^{[l]}{)}^2 \\ Frobeniusnorm弗罗贝尼乌斯范数 \end{gathered}$$

1.5 为什么正则化可以减少过拟合？

1.6 dropout随机失活正则化

dropout：随机概率值作为每一层结点的存在概率，被删除的结点与之相关的进出路线全部删除，最后得到一个节点更少、规模更小的额网络。

#layer l = 3, keep-prob = 0.8
d3 = np.random.rand(a3.shape[0],a3.shape[1])<keep_prob
a3 = np.multiply(a3,d3)  #a3 *=d3
a3 /= keep-prob

inverted dropout 反向随机失活

随机失活应用于训练集train set，不适用于测试集test set，因为我们想要测试集的结果保持稳定。

1.7 理解dropout

如果你担心一些层比其它层更容易发生过拟合，那么你可以把这些层的keep-prob值设置地比其它层更低。缺点是为了参加交叉验证，你需要搜索更多的超级参数。

另一种方法是只在一些层用dropout，而在另一些层不用dropout。

dropout主要用在计算机视觉领域，因为没有足够多的数据，所以经常出现过拟合。

dropout的一大缺点在于代价函数J不再明确定义，每次迭代都会随机移除一些结点

1.8 其他正则化方法

增加训练集的简易方法（数据增强）：翻转图片、随意更改并剪切

early stopping：提早停止训练神经网络

1.9 归一化输入

数据的标准化：
$$\begin{gathered} x^{\prime }=\frac{x?\mu }{\sigma } \\ \mu =\frac{1}{m}\sum _{i=1}^m{x}^{(i)},\sigma =\frac{1}{m}\sum _{i=1}^m(x^{(i)}?\mu {)}^2 \end{gathered}$$

1.10 梯度消失和梯度爆炸

1.11 神经网络的权重初始化

1.12 梯度的数值逼近

$$\begin{gathered} g(\theta )\approx \frac{f(\theta +?)?f(\theta ??)}{2?}(双边公差)O({?}^2) \\ g(\theta )\approx \frac{f(\theta +?)?f(\theta ??)}{?}(单边公差)O(?) \end{gathered}$$

双边误差公式的结果比单边的更准确

1.13 梯度检验

$$\begin{gathered} foreachi: \\ d{\theta }_{approx}^{[i]}=\frac{J({\theta }_1,{\theta }_2,\dots \dots ,{\theta }_i+?,\dots \dots )?J({\theta }_1,{\theta }_2,\dots \dots ,{\theta }_i??,\dots \dots )}{2?} \\ \approx d{\theta }^{[i]}=\frac{?J}{?{\theta }_i} \\ check:\frac{||d{\theta }_{approx}?d\theta |{|}_2}{||d{\theta }_{approx}|{|}_2+||d\theta |{|}_2}\approx 10^{?7}great! \end{gathered}$$

1.14 关于梯度检验实现的注记

正则化 + 梯度检验

梯度检验和dropout不能同时使用

2.1 mini-batch 梯度下降法

5000000样本的训练集，分为1000个batch，每个batch有5000个样本。

每个epoch（代）都会遍历所有的样本一次（1000次batch），进行一次梯度下降，多次循环训练集需要多个epoch。

2.2 理解mini-batch 梯度下降法

if mini-batch size = m:batch gradient descent ( X { 1 } , Y { 1 } ) = ( X , Y ) (X^{\{1\}},Y^{\{1\}}) = (X,Y) (X{1},Y{1})=(X,Y)

训练一次的时间可能过长

if mini-batch size = 1:stochastic gradient descent ( X { 1 } , Y { 1 } ) = ( X ( 1 ) , Y ( 1 ) ) (X^{\{1\}},Y^{\{1\}}) = (X^{(1)},Y^{(1)}) (X{1},Y{1})=(X(1),Y(1))

但是效率过于低下

2.3 指数加权平均

$V_t=\beta V_{t?1}+(1?\beta ){\theta }_t$

2.4 理解指数加权平均

2.5 指数加权平均的偏差修正

$V_t=\frac{\beta V_{t?1}+(1?\beta ){\theta }_t}{1?{\beta }^t}$

主要是修正初期的误差

2.6 动量梯度下降法 gradient descent with momentum

问题：纵轴波动过大，横轴前进较小

目标：纵轴降低波动，横轴加速前进

类比：碗里面的小球获得加速度而加速前进

2.7 RMSprop

$$\begin{gathered} S_{dW}=\beta S_{dW}+(1?\beta )(dW{)}^2 \\ {S}_{db}=\beta S_{db}+(1?\beta )(db{)}^2 \\ W:=W?\alpha \frac{dW}{\sqrt{S_{dW}+?}} \\ b:=b?\alpha \frac{db}{\sqrt{S_{db}+?}} \\ W方向斜率较小，dW较小，S_{dW}较小，W的更新较大 \\ b方向斜率较大，db较大，S_{db}较大，b的更新较小 \end{gathered}$$

2.8 Adam优化算法（adaptive moment estimation）

Adam算法结合了momentum算法和RMSprop算法
$$\begin{gathered} V_{dW}=0,V_{db}=0,S_{dW}=0,S_{db}=0 \\ {V}_{dW}={\beta }_1{V}_{dW}+(1?{\beta }_1)dW \\ {V}_{db}={\beta }_1{V}_{db}+(1?{\beta }_1)dbmomentum \\ {S}_{dW}={\beta }_2{S}_{dW}+(1?{\beta }_2)(dW{)}^2 \\ {S}_{db}={\beta }_2{S}_{db}+(1?{\beta }_2)(db{)}^{2}RMS \\ {V}_{dW}^{correct}=\frac{V_{dW}}{1?{\beta }_1^t},V_{db}^{correct}=\frac{V_{db}}{1?{\beta }_1^t} \\ {S}_{dW}^{correct}=\frac{S_{dW}}{1?{\beta }_2^t},S_{db}^{correct}=\frac{S_{db}}{1?{\beta }_2^t} \\ W:=W?\alpha \frac{V_{dW}^{correct}}{\sqrt{S_{dW}^{correct}+?}} \\ b:=b?\alpha \frac{V_{db}^{correct}}{\sqrt{S_{db}^{correct}+?}} \end{gathered}$$

2.9 学习率衰减

1 epoch = 1 pass through data
$$\begin{gathered} \alpha =\frac{1}{1+deca{y}_{rate}?epoc{h}_{num}}?{\alpha }_0 \\ {\alpha }_0=0.2,deca{y}_{rate}=1 \end{gathered}$$

其他衰减方法
$$\begin{gathered} \alpha =0.95^{epoc{h}_{num}}{\alpha }_0 \\ \alpha =\frac{{\alpha }_0}{epoc{h}_{num}}?{\alpha }_{0}or\frac{k}{\sqrt{t}}?{\alpha }_0（t是mini?batch的批次） \\ 离散衰减学习率 \end{gathered}$$

2.10 局部最优的问题

高维度空间更可能存在的是鞍点，而不是局部最优。

平稳段（导数接近于0的区域）的学习率会很慢

3.1 调试处理（tuning process）

超参数调节：hyperparameters
$$\alpha ,\beta ,{\beta }_1,{\beta }_2,layers,hiddenu,learningdecayrate,mini?batchsize$$

3.2 为超参数选择合适的范围

$\beta$:从粗到细的取值方法、不均匀的取值方法（越接近1取值越多）

3.3 超参数运用的实践（pandas vs caviar)

3.4 正则化网络的激活函数

使隐藏单元的均值和方差标准化

3.5 将batch norm拟合进神经网络

3.6 batch norm为什么奏效？

首先在于归一化（均值为0，方差为1）在做类似的工作

其次可以使权重比你的网络更滞后或更深层

covariate shift：使你的数据改变分布

batch norm限制了在前层的参数更新会影响数值分布的程度（均值和方差是可控的），减少了输入值改变的问题，减弱了前层参数的作用与后层参数的作用之间的联系。使得不同层之间稍稍独立于其它层，这有助于加速整个网络的学习。

batch norm还有轻微的正则化效果，类似于dropout，因为给隐藏单元添加了噪音，这迫使后部单元不过分依赖任何一个隐藏单元。因为噪音很小，所以是轻微的正则化效果，可以将batch norm和dropout两者共同使用。

通过应用较大的mini batch size，减少了噪音，因此减少了正则化效果。

3.7 测试时的batch norm

在训练时，$\mu$和$\sigma$是在整个mini-batch上计算出来的，多个mini-batch自然会有多个$\mu$和$\sigma$。

测试时，需要逐一处理样本,只需要一个$\mu$和$\sigma$，此时选择指数加权平均等方法估算

使用batch归一化，能够训练更深的网络，让你的算法运行速度更快。

3.8 softmax回归

softmax回归：logistic回归的一般形式，多分类识别，将logistic回归的两类拓展到多类
$$\begin{gathered} z^{[l]}=w^{[l]}{a}^{[l?1]}+b^{[l]} \\ activationfunction:t=e^{z^{[l]}} \\ {a}_i^{[l]}=\frac{t_i}{{\sum }_i{t}_i} \end{gathered}$$
最后输出的向量和为1，代表不同输出结果的概率大小。

softmax分类器在没有隐藏层的情况下，有类似线性的决策边界，但可以有超过两个分类

3.9 训练一个softmax分类器

$$\begin{gathered} z^{[l]}=?\begin{array}{c}5\\ 2\\ ?1\\ 3\end{array}?,t=?\begin{array}{c}{e}^5\\ e^2\\ e^{?1}\\ e^3\end{array}? \\ {g}^{[l]}(z^{[l]})=?\begin{array}{c}\frac{e^5}{e^5+e^2+e^{?1}+e^3}\\ \frac{e^2}{e^5+e^2+e^{?1}+e^3}\\ \frac{e^{?1}}{e^5+e^2+e^{?1}+e^3}\\ \frac{e^3}{e^5+e^2+e^{?1}+e^3}\end{array}?=?\begin{array}{c}0.842\\ 0.042\\ 0.002\\ 0.114\end{array}? \end{gathered}$$

hard max:[1 0 0 0] (z最大的元素输出为1，其他元素输出为0)

3.10 深度学习框架

寻找合适的深度学习框架：易于编程、运行速度快、开源且良好的管理

3.11 tensorflow

import numpy as np
import tensorflow as tf

coefficients = np.array([[1],[-20],[25]])

w = tf.Variable([0],dtrpe = tf.float32)
x = tf.placeholder(tf.float32,[3,1])
cost = x[0][0]*w**2 + x[1][0]*w + x[2][0]
train = tf.train.GradientDescentOptimizer(0.01).minimize(cost)
init = tf.global_variables_initializer()
session = tf.Session()  #with tf.Session() as session:
session.run(init)			#session.run(init)
print(session.run(w))		#print(session.run(w))

for i in range(1000):
    session.run(train,feed_dict={x:coefficients})
print(session.run(w))