回归定义和应用例子
回归定义
Regression 就是找到一个函数 f u n c t i o n function function ,通过输入特征 x x x,输出一个数值 S c a l a r Scalar Scalar。
应用举例
- 股市预测(Stock market forecast)
- 输入:过去10年股票的变动、新闻咨询、公司并购咨询等
- 输出:预测股市明天的平均值
- 自动驾驶(Self-driving Car)
- 输入:无人车上的各个sensor的数据,例如路况、测出的车距等
- 输出:方向盘的角度
- 商品推荐(Recommendation)
- 输入:商品A的特性,商品B的特性
- 输出:购买商品B的可能性
- Pokemon精灵攻击力预测(Combat Power of a pokemon):
- 输入:进化前的CP值、物种(Bulbasaur)、血量(HP)、重量(Weight)、高度(Height)
- 输出:进化后的CP值
模型步骤
- step1:模型假设,选择模型框架(线性模型)
- step2:模型评估,如何判断众多模型的好坏(损失函数)
- step3:模型优化,如何筛选最优的模型(梯度下降)
Step 1:模型假设 - 线性模型
一元线性模型(单个特征)
以一个特征
x
c
p
x_{cp}
xcp? 为例,线性模型假设
y
=
b
+
w
?
x
c
p
y = b + w·x_{cp}
y=b+w?xcp? ,所以
w
w
w 和
b
b
b 可以猜测很多模型:
f
1
:
y
=
10.0
+
9.0
?
x
c
p
f
2
:
y
=
9.8
+
9.2
?
x
c
p
f
3
:
y
=
?
0.8
?
1.2
?
x
c
p
?
?
?
f_1: y = 10.0 + 9.0·x_{cp} \\ f_2: y = 9.8 + 9.2·x_{cp} \\ f_3: y = - 0.8 - 1.2·x_{cp} \\ ···
f1?:y=10.0+9.0?xcp?f2?:y=9.8+9.2?xcp?f3?:y=?0.8?1.2?xcp????
虽然可以做出很多假设,但在这个例子中,显然 f 3 : y = ? 0.8 ? 1.2 ? x c p f_3: y = - 0.8 - 1.2·x_{cp} f3?:y=?0.8?1.2?xcp? 的假设是不合理的,不能进化后CP值是个负值吧~~
多元线性模型(多个特征)
在实际应用中,输入特征肯定不止 x c p x_{cp} xcp? 这一个。例如,进化前的CP值、物种(Bulbasaur)、血量(HP)、重量(Weight)、高度(Height)等,特征会有很多。
所以我们假设 线性模型 Linear model: y = b + ∑ w i x i y = b + \sum w_ix_i y=b+∑wi?xi?
- x i x_i xi?:就是各种特征(fetrure) x c p , x h p , x w , x h , ? ? ? x_{cp},x_{hp},x_w,x_h,··· xcp?,xhp?,xw?,xh?,???
- w i w_i wi?:各个特征的权重 w c p , w h p , w w , w h , ? ? w_{cp},w_{hp},w_w,w_h,·· wcp?,whp?,ww?,wh?,??
- b b b:偏移量
注意:接下来的内容需要看清楚是【单个特征】还是【多个特征】的示例
Step 2:模型评估 - 损失函数
【单个特征】: x c p x_{cp} xcp?
收集和查看训练数据
这里定义 x 1 x^1 x1 是进化前的CP值, y ^ 1 \hat{y}^1 y^?1 进化后的CP值, ^ \hat{} ^ 所代表的是真实值
将10组原始数据在二维图中展示,图中的每一个点 ( x c p n , y ^ n ) (x_{cp}^n,\hat{y}^n) (xcpn?,y^?n) 对应着 进化前的CP值 和 进化后的CP值。
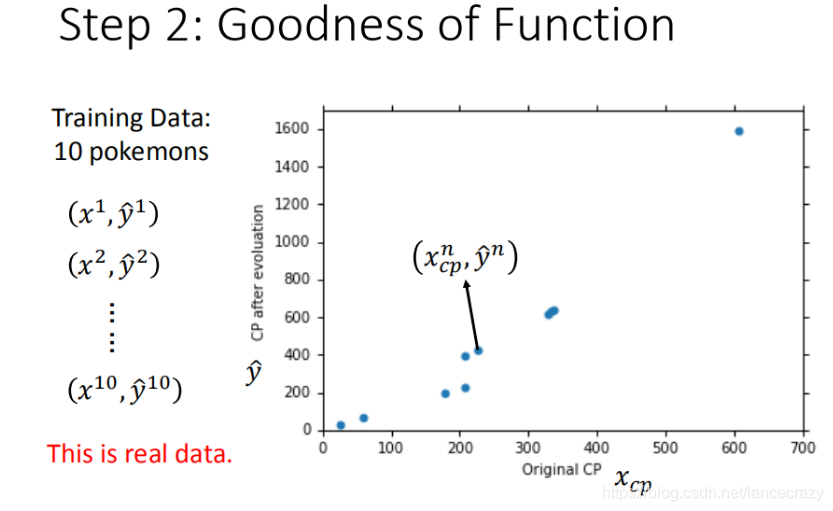
如何判断众多模型的好坏
直接看公式推导的过程:
L ( f ) = ∑ n = 1 10 ( y ^ n ? f ( x c p n ) ) 2 , 将 【 f ( x ) = y 】 , 【 y = b + w ? x c p 】 代 入 = ∑ n = 1 10 ( y ^ n ? ( b + w ? x c p ) ) 2 \begin{aligned} L(f) & = \sum_{n=1}^{10}\left ( \hat{y}^n - f(x_{cp}^n) \right )^2,将【f(x) = y】, 【y= b + w·x_{cp}】代入 \\ & = \sum_{n=1}^{10}\left ( \hat{y}^n - (b + w·x_{cp}) \right )^2\\ \end{aligned} L(f)?=n=1∑10?(y^?n?f(xcpn?))2,将【f(x)=y】,【y=b+w?xcp?】代入=n=1∑10?(y^?n?(b+w?xcp?))2?
最终定义 损失函数 Loss function: L ( w , b ) = ∑ n = 1 10 ( y ^ n ? ( b + w ? x c p ) ) 2 L(w,b)= \sum_{n=1}^{10}\left ( \hat{y}^n - (b + w·x_{cp}) \right )^2 L(w,b)=∑n=110?(y^?n?(b+w?xcp?))2
Step 3:最佳模型 - 梯度下降
【单个特征】: x c p x_{cp} xcp?
如何筛选最优的模型(参数w,b)
已知损失函数是 L ( w , b ) = ∑ n = 1 10 ( y ^ n ? ( b + w ? x c p ) ) 2 L(w,b)= \sum_{n=1}^{10}\left ( \hat{y}^n - (b + w·x_{cp}) \right )^2 L(w,b)=∑n=110?(y^?n?(b+w?xcp?))2 ,需要找到一个令结果最小的 f ? f^* f?,在实际的场景中,我们遇到的参数肯定不止 w w w, b b b。
先从最简单的只有一个参数 w w w入手,定义 w ? = a r g ? min ? ? x L ( w ) w^* = arg\ \underset{x}{\operatorname{\min}} L(w) w?=arg?xmin?L(w)
首先在这里引入一个概念 学习率 :移动的步长,如图7中 η \eta η
- 步骤1:随机选取一个 w 0 w^0 w0
- 步骤2:计算微分,也就是当前的斜率,根据斜率来判定移动的方向
- 大于0向右移动(增加 w w w)
- 小于0向左移动(减少 w w w)
- 步骤3:根据学习率移动
- 重复步骤2和步骤3,直到找到最低点
步骤1中,我们随机选取一个 w 0 w^0 w0,如图8所示,我们有可能会找到当前的最小值,并不是全局的最小值,这里我们保留这个疑问,后面解决。
解释完单个模型参数
w
w
w,引入2个模型参数
w
w
w 和
b
b
b , 其实过程是类似的,需要做的是偏微分,过程如图9所示,偏微分的求解结果文章后面会有解释,详细的求解过程自行Google。

梯度下降推演最优模型的过程
如果把 w w w 和 b b b 在图形中展示:
- 每一条线围成的圈就是等高线,代表损失函数的值,颜色约深的区域代表的损失函数越小
- 红色的箭头代表等高线的法线方向
梯度下降算法在现实世界中面临的挑战
其实还会有其他的问题:
- 问题1:当前最优(Stuck at local minima)
- 问题2:等于0(Stuck at saddle point)
- 问题3:趋近于0(Very slow at the plateau)
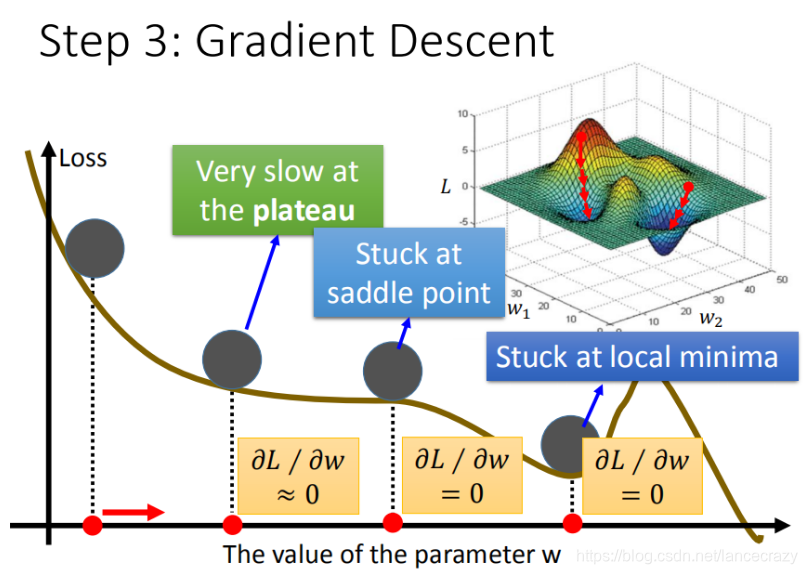
注意:其实在线性模型里面都是一个碗的形状(山谷形状),梯度下降基本上都能找到最优点,但是再其他更复杂的模型里面,就会遇到 问题2 和 问题3 了
如何验证训练好的模型的好坏
使用训练集和测试集的平均误差来验证模型的好坏
过拟合问题出现
在模型上,我们再可以进一部优化,使用更高次方的模型,如图所示
在训练集上面表现更为优秀的模型,为什么在测试集上效果反而变差了?这就是模型在训练集上过拟合的问题。
如图所示,每一个模型结果都是一个集合,
5
次
模
型
包
?
4
次
模
型
?
3
次
模
型
5次模型包 \supseteq 4次模型 \supseteq 3次模型
5次模型包?4次模型?3次模型
所以在4次模型里面找到的最佳模型,肯定不会比5次模型里面找到更差
将错误率结果图形化展示,发现3次方以上的模型,已经出现了过拟合的现象:
步骤优化
输入更多Pokemons数据,相同的起始CP值,但进化后的CP差距竟然是2倍。如图21,其实将Pokemons种类通过颜色区分,就会发现Pokemons种类是隐藏得比较深得特征,不同Pokemons种类影响了进化后的CP值的结果。
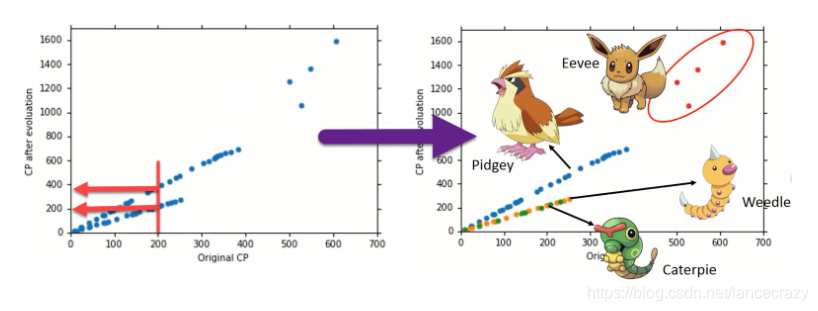
Step1优化:2个input的四个线性模型是合并到一个线性模型中
通过对 Pokemons种类 判断,将 4个线性模型 合并到一个线性模型中
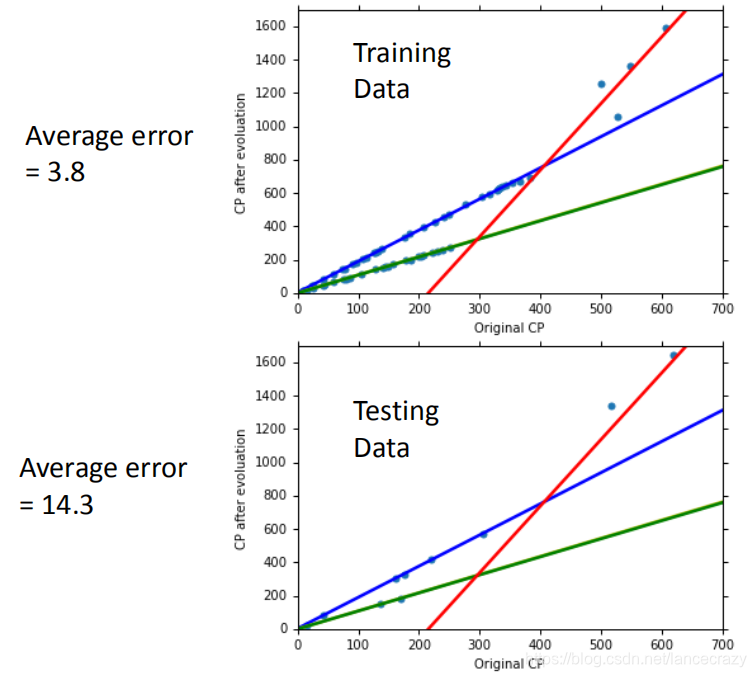
Step2优化:如果希望模型更强大表现更好(更多参数,更多input)
在最开始我们有很多特征,图形化分析特征,将血量(HP)、重量(Weight)、高度(Height)也加入到模型中
Step3优化:加入正则化
更多特征,但是权重
w
w
w 可能会使某些特征权值过高,仍旧导致overfitting,所以加入正则化

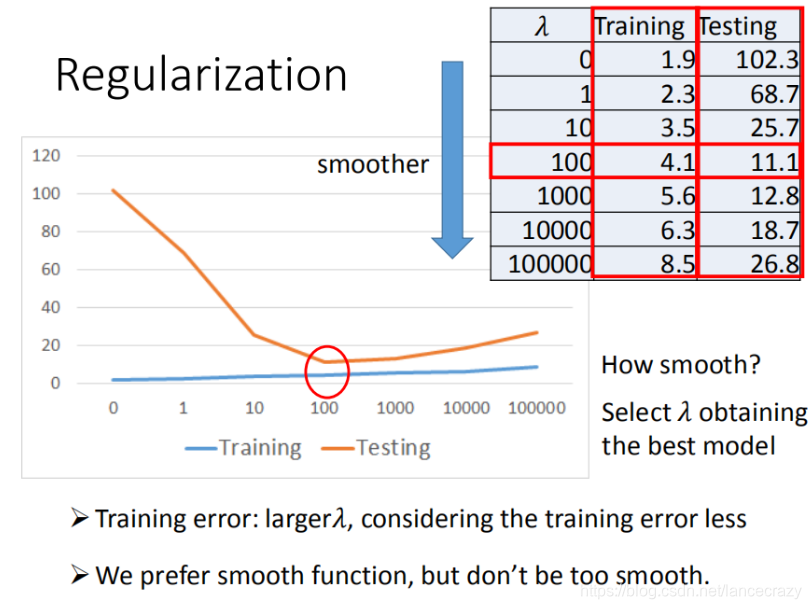
- w w w 越小,表示 f u n c t i o n function function 较平滑的, f u n c t i o n function function输出值与输入值相差不大
- 在很多应用场景中,并不是 w w w 越小模型越平滑越好,但是经验值告诉我们 w w w 越小大部分情况下都是好的。
- b b b 的值接近于0 ,对曲线平滑是没有影响
总结
- Pokemon:原始的CP值极大程度的决定了进化后的CP值,但可能还有其他的一些因素。
- Gradient descent:梯度下降的做法;后面会讲到它的理论依据和要点。
- Overfitting和Regularization:过拟合和正则化,主要介绍了表象;后面会讲到更多这方面的理论
实验
import numpy as np
import matplotlib.pyplot as plt
from pylab import mpl
# matplotlib没有中文字体,动态解决
plt.rcParams['font.family'] = 'Arial Unicode MS'
plt.rcParams['font.sans-serif'] = ['MicroSoft YaHei']
x_data = [338., 333., 328., 207., 226., 25., 179., 60., 208., 606.]
y_data = [640., 633., 619., 393., 428., 27., 193., 66., 226., 1591.]
x_d = np.asarray(x_data)
y_d = np.asarray(y_data)
x = np.arange(-200, -100, 1)
y = np.arange(-5, 5, 0.1)
Z = np.zeros((len(x), len(y)))
X, Y = np.meshgrid(x, y)
# loss
for i in range(len(x)):
for j in range(len(y)):
b = x[i]
w = y[j]
Z[j][i] = 0 # meshgrid吐出结果:y为行,x为列
for n in range(len(x_data)):
Z[j][i] += (y_data[n] - b - w * x_data[n]) ** 2
Z[j][i] /= len(x_data)
# linear regression
b = -140
w = -2
# b=-2
# w=0.01
lr = 0.00001
iteration = 500000
b_history = [b]
w_history = [w]
loss_history = []
import time
start = time.time()
for i in range(iteration):
m = float(len(x_d))
y_hat = w * x_d +b
loss = np.dot(y_d - y_hat, y_d - y_hat) / m
grad_b = -2.0 * np.sum(y_d - y_hat) / m
grad_w = -2.0 * np.dot(y_d - y_hat, x_d) / m
# update param
b -= lr * grad_b
w -= lr * grad_w
b_history.append(b)
w_history.append(w)
loss_history.append(loss)
if i % 10000 == 0:
print("Step %i, w: %0.4f, b: %.4f, Loss: %.4f" % (i, w, b, loss))
end = time.time()
print("大约需要时间:",end-start)
Step 0, w: 5.9135, b: -139.9775, Loss: 1803371.0000
Step 10000, w: 2.5378, b: -142.6135, Loss: 10778.7443
Step 20000, w: 2.5449, b: -145.0974, Loss: 10717.0300
Step 30000, w: 2.5517, b: -147.4467, Loss: 10661.8255
Step 40000, w: 2.5581, b: -149.6685, Loss: 10612.4440
Step 50000, w: 2.5641, b: -151.7700, Loss: 10568.2713
Step 60000, w: 2.5698, b: -153.7575, Loss: 10528.7581
Step 70000, w: 2.5752, b: -155.6373, Loss: 10493.4127
Step 80000, w: 2.5803, b: -157.4151, Loss: 10461.7957
Step 90000, w: 2.5851, b: -159.0966, Loss: 10433.5137
Step 100000, w: 2.5897, b: -160.6870, Loss: 10408.2149
Step 110000, w: 2.5940, b: -162.1911, Loss: 10385.5846
Step 120000, w: 2.5981, b: -163.6137, Loss: 10365.3415
Step 130000, w: 2.6020, b: -164.9592, Loss: 10347.2336
Step 140000, w: 2.6057, b: -166.2317, Loss: 10331.0358
Step 150000, w: 2.6091, b: -167.4352, Loss: 10316.5465
Step 160000, w: 2.6124, b: -168.5736, Loss: 10303.5856
Step 170000, w: 2.6155, b: -169.6501, Loss: 10291.9919
Step 180000, w: 2.6184, b: -170.6684, Loss: 10281.6210
Step 190000, w: 2.6212, b: -171.6314, Loss: 10272.3441
Step 200000, w: 2.6238, b: -172.5422, Loss: 10264.0458
Step 210000, w: 2.6263, b: -173.4037, Loss: 10256.6227
Step 220000, w: 2.6286, b: -174.2184, Loss: 10249.9827
Step 230000, w: 2.6308, b: -174.9890, Loss: 10244.0430
Step 240000, w: 2.6329, b: -175.7178, Loss: 10238.7299
Step 250000, w: 2.6349, b: -176.4071, Loss: 10233.9772
Step 260000, w: 2.6368, b: -177.0591, Loss: 10229.7259
Step 270000, w: 2.6385, b: -177.6757, Loss: 10225.9230
Step 280000, w: 2.6402, b: -178.2588, Loss: 10222.5212
Step 290000, w: 2.6418, b: -178.8104, Loss: 10219.4782
Step 300000, w: 2.6433, b: -179.3320, Loss: 10216.7563
Step 310000, w: 2.6447, b: -179.8254, Loss: 10214.3214
Step 320000, w: 2.6461, b: -180.2921, Loss: 10212.1434
Step 330000, w: 2.6473, b: -180.7334, Loss: 10210.1951
Step 340000, w: 2.6485, b: -181.1508, Loss: 10208.4523
Step 350000, w: 2.6497, b: -181.5456, Loss: 10206.8934
Step 360000, w: 2.6507, b: -181.9190, Loss: 10205.4988
Step 370000, w: 2.6517, b: -182.2721, Loss: 10204.2514
Step 380000, w: 2.6527, b: -182.6061, Loss: 10203.1356
Step 390000, w: 2.6536, b: -182.9220, Loss: 10202.1375
Step 400000, w: 2.6545, b: -183.2207, Loss: 10201.2446
Step 410000, w: 2.6553, b: -183.5033, Loss: 10200.4460
Step 420000, w: 2.6561, b: -183.7706, Loss: 10199.7315
Step 430000, w: 2.6568, b: -184.0233, Loss: 10199.0925
Step 440000, w: 2.6575, b: -184.2624, Loss: 10198.5208
Step 450000, w: 2.6581, b: -184.4885, Loss: 10198.0095
Step 460000, w: 2.6587, b: -184.7023, Loss: 10197.5520
Step 470000, w: 2.6593, b: -184.9046, Loss: 10197.1429
Step 480000, w: 2.6599, b: -185.0959, Loss: 10196.7769
Step 490000, w: 2.6604, b: -185.2768, Loss: 10196.4495
大约需要时间: 12.86750602722168
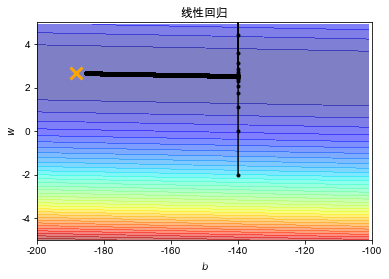
# plot the figure
plt.contourf(x, y, Z, 50, alpha=0.5, cmap=plt.get_cmap('jet')) # 填充等高线
plt.plot([-188.4], [2.67], 'x', ms=12, mew=3, color="orange")
plt.plot(b_history, w_history, 'o-', ms=3, lw=1.5, color='black')
plt.xlim(-200, -100)
plt.ylim(-5, 5)
plt.xlabel(r'$b$')
plt.ylabel(r'$w$')
plt.title("线性回归")
plt.show()
? 
?
# linear regression
b = -120
w = -10
lr = 1
iteration = 100000
b_history = [b]
w_history = [w]
lr_b=0
lr_w=0
import time
start = time.time()
for i in range(iteration):
b_grad=0.0
w_grad=0.0
for n in range(len(x_data)):
b_grad= b_grad-2.0*(y_data[n]-n-w*x_data[n])*1.0
w_grad= w_grad-2.0*(y_data[n]-n-w*x_data[n])*x_data[n]
lr_b=lr_b+b_grad**2
lr_w=lr_w+w_grad**2
# update param
b -= lr/np.sqrt(lr_b) * b_grad
w -= lr /np.sqrt(lr_w) * w_grad
b_history.append(b)
w_history.append(w)
# plot the figure
plt.contourf(x, y, Z, 50, alpha=0.5, cmap=plt.get_cmap('jet')) # 填充等高线
plt.plot([-188.4], [2.67], 'x', ms=12, mew=3, color="orange")
plt.plot(b_history, w_history, 'o-', ms=3, lw=1.5, color='black')
plt.xlim(-200, -100)
plt.ylim(-5, 5)
plt.xlabel(r'$b$')
plt.ylabel(r'$w$')
plt.title("线性回归")
plt.show()
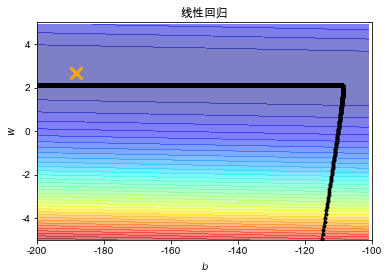
?