[人工智能]机器学习（五） 神经网络

机器学习（五） 神经网络

1.单隐层神经网络

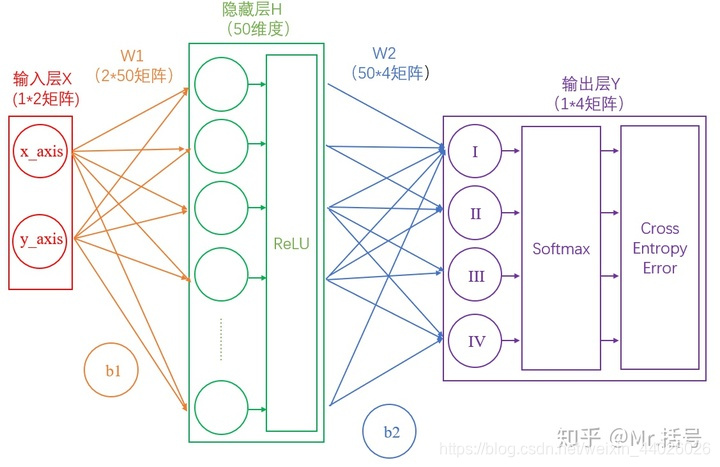
1.1 从输入层到隐藏层

连接输入层和隐藏层的是W1和b1。由X计算得到H十分简单，就是矩阵运算：
$$H=X?W1+b1$$

1.2 从隐藏层到输出层

连接隐藏层和输出层的是W2和b2。同样是通过矩阵运算进行的：
$$Y=H?W2+b2$$
通过上述两个线性方程的计算，我们就能得到最终的输出Y了，但是如果你还对线性代数的计算有印象的话，应该会知道：一系列线性方程的运算最终都可以用一个线性方程表示。也就是说，上述两个式子联立后可以用一个线性方程表达。对于两次神经网络是这样，就算网络深度加到100层，也依然是这样。这样的话神经网络就失去了意义。所以这里要对网络注入灵魂：激活层。

1.3 激活层

简而言之，激活层是为矩阵运算的结果添加非线性的。常用的激活函数有三种，分别是阶跃函数、Sigmoid和ReLU：

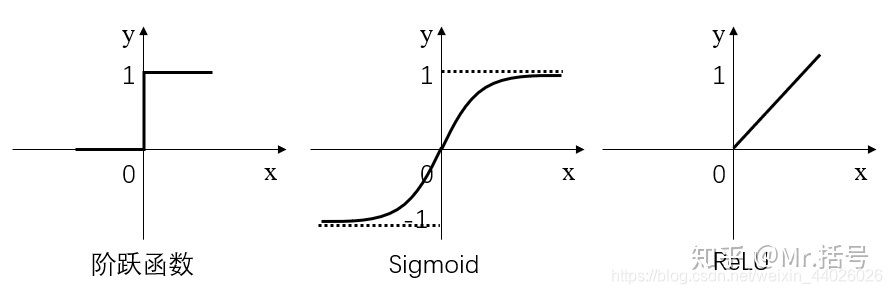
• 阶跃函数：当输入小于等于0时，输出0；当输入大于0时，输出1。
• Sigmoid：当输入趋近于正无穷/负无穷时，输出无限接近于1/0。
• ReLU：当输入小于0时，输出0；当输入大于0时，输出等于输入。

其中，阶跃函数输出值是跳变的，且只有二值，较少使用；
Sigmoid函数在当x的绝对值较大时，曲线的斜率变化很小（梯度消失），并且计算较复杂；
ReLU是当前较为常用的激活函数。
激活函数具体是怎么计算的呢？假如经过公式H=X*W1+b1计算得到的H值为：(1,-2,3,-4,7…)，那么经过阶跃函数激活层后就会变为(1,0,1,0,1…)，经过ReLU激活层之后会变为(1,0,3,0,7…)。需要注意的是，每个隐藏层计算（矩阵线性运算）之后，都需要加一层激活层，要不然该层线性计算是没有意义的。

1.4 输出的正规化

由上面分析可知，输出Y的值可能会是(3,1,0.1,0.5)这样的矩阵，诚然我们可以找到里边的最大值“3”，从而找到对应的分类为I，但是这并不直观。我们想让最终的输出为概率，也就是说可以生成像(90%,5%,2%,3%)这样的结果，这样做不仅可以找到最大概率的分类，而且可以知道各个分类计算的概率值。我们将使用这个计算公式做输出结果正规化处理的层叫做“Softmax”层。
计算公式如下：
$$S_j=\frac{e^{a_j}}{{\sum }_{k=1}^N{e}^{a_k}}$$
他能够保证：
所有的值都是 [0, 1] 之间的（因为概率必须是 [0, 1]）所有的值加起来等于 1
从概率的角度解释 softmax 的话，就是：
$$S_j=P\left(y=j|a\right)$$
简单来说分三步进行：
（1）以e为底对所有元素求指数幂；
（2）将所有指数幂求和；
（3）分别将这些指数幂与该和做商。
这样求出的结果中，所有元素的和一定为1，而每个元素可以代表概率值。

1.5 如何衡量输出的好坏

通过Softmax层之后，我们得到了I，II，III和IV这四个类别分别对应的概率，但是要注意，这是神经网络计算得到的概率值结果，而非真实的情况。
比如，Softmax输出的结果是(90%,5%,3%,2%)，真实的结果是(100%,0,0,0)。虽然输出的结果可以正确分类，但是与真实结果之间是有差距的，一个优秀的网络对结果的预测要无限接近于100%，为此，我们需要将Softmax输出结果的好坏程度做一个“量化”。一种直观的解决方法，是用1减去Softmax输出的概率，比如1-90%=0.1。
不过更为常用且巧妙的方法是，求对数的负数。还是用90%举例，对数的负数就是：-log0.9=0.046可以想见，概率越接近100%，该计算结果值越接近于0，说明结果越准确，该输出叫做“交叉熵损失（Cross Entropy Error）”。我们训练神经网络的目的，就是尽可能地减少这个“交叉熵损失”。

1.6 反向传播与参数优化

上面讲述了神经网络的正向传播过程。一句话总结一下：神经网络的传播都是形如Y=WX+b的矩阵运算；为了给矩阵运算加入非线性，需要在隐藏层中加入激活层；输出层结果需要经过Softmax层处理为概率值，并通过交叉熵损失来量化当前网络的优劣。算出交叉熵损失后，就要开始反向传播了。其实反向传播就是一个参数优化的过程，优化对象就是网络中的所有W和b（因为其他所有参数都是确定的）。神经网络的神奇之处，就在于它可以自动做W和b的优化，在深度学习中，参数的数量有时会上亿，不过其优化的原理和我们这个两层神经网络是一样的。

反向传播就是计算偏微分，信息会从神经网络的高层向底层反向传播，并在这个过程中根据输出来调整权重。反向传播的思路是拿到损失函数给出的值，从结果开始，顺藤摸瓜，逐步求导，偏微分逐步地发现每一个参数应该往哪个方向调整才能减小损失。