简单概括:所谓回归,即找到一个function(函数),对其输入特征(自变量),再输出一个预测值(因变量)
下文拿预测Pokemon精灵的攻击力作为例子讲解回归的步骤哈哈哈哈哈哈
机器学习(×)
神奇宝贝(√)
我们希望的是:
输入:进化前的CP值,物种,血量,重量,高度
输出:进化后的CP值
做回归一般经历如下三个步骤:
● step1:模型假设,选择模型
●step2:引入损失函数评估模型好坏
●step3:梯度下降筛选最优模型
Step1:模型假设,选择模型
1.一元线性模型(单变量输入)
考虑方程:
y
=
b
+
w
x
c
p
y=b+wx_{cp}
y=b+wxcp?
当精灵进化时,cp值只增不减,所以可以排除w<0的所有情况。
这其实就是简单的一次函数,当给定当前cp值,代入方程便可求得一个y,即升级后的cp值
接下来我们更复杂的情况
2.多元线性模型(多变量输入)
精灵进化后cp值的确定,当然不能仅依靠现有的cp值,还可能与精灵的血量,物种,重量,高度等特征有关,所以我们引入多元线性模型:
y
=
b
+
∑
w
i
x
i
y=b+\sum{w_ix_i}
y=b+∑wi?xi?
其中b表示偏移量,w表示各个特征的权重,x表示特征数值。
Step2:引入损失函数评估模型好坏
所谓损失函数(loss function),就是用来评估选择的模型的好坏程度的方程,用损失函数可以衡量模型预测值与真实值之间的差异大小。
● 一元线性模型的损失函数
对于简单的一元线性模型,我们定义其模型函数如下:
f
(
x
c
p
)
=
b
+
w
x
c
p
f\left( x_{cp} \right) =b+wx_{cp}
f(xcp?)=b+wxcp?
以我们最朴素的直觉,想验证这些预测的进化后的cp值准不准,需要拿真实情况下进化后的cp值来作比较。我们假设抓到了10只精灵,并记录了他们进化前后的cp值,表示如下:
(
x
1
,
y
^
1
)
,
(
x
2
,
y
^
2
)
,
(
x
3
,
y
^
3
)
.
.
.
.
.
.
(
x
10
,
y
^
10
)
\left( x_1,\hat{y}_1 \right) ,\left( x_2,\hat{y}_2 \right) ,\left( x_3,\hat{y}_3 \right) ......\left( x_{10},\hat{y}_{10} \right)
(x1?,y^?1?),(x2?,y^?2?),(x3?,y^?3?)......(x10?,y^?10?)
其中x项表示进化前的cp值,y项表示进化后的cp值,注意这些都是真实数据,是人为记录下来的。
根据上面的直觉,我们可以考虑用距离,来衡量预测值与真实值之间的差异,从而引入损失函数:
L
(
f
)
=
∑
n
=
1
10
(
y
^
n
?
f
(
x
n
)
)
2
L\left( f \right) =\sum_{n=1}^{10}{\left( \hat{y}_n-f\left( x_n \right) \right) ^2}
L(f)=n=1∑10?(y^?n??f(xn?))2
进一步展开,即:
L
(
w
,
b
)
=
∑
n
=
1
10
(
y
^
n
?
f
(
x
n
)
)
2
=
∑
n
=
1
10
(
y
^
n
?
(
b
+
w
x
n
)
)
2
L\left( w,b\right) =\sum_{n=1}^{10}{\left( \hat{y}_n-f\left( x_n \right) \right) ^2}=\sum_{n=1}^{10}{\left( \hat{y}_n-\left( b+wx_n \right) \right) ^2}
L(w,b)=n=1∑10?(y^?n??f(xn?))2=n=1∑10?(y^?n??(b+wxn?))2
这个方程看似复杂,但其实也是符合直觉的,简单来说,就是将真实值与预测值作差,平方后,再求和,至于平方,是为了避免真实值小于预测值从而出现负数这种情况,因为出现负数会导致最终损失函数的值偏小,从而影响客观判断。
Step3:梯度下降筛选最优模型
我们依然考虑一元线性模型
我们现在假设,在上述损失函数中,w,b我们仍未确定,也就是说,我们需要确定具体的w,b的值,使得损失函数最小,这是我们不变的目标。即:
w
?
,
b
?
=
a
r
g
?
min
?
w
,
b
∑
n
=
1
10
(
y
^
n
?
(
b
+
w
x
n
)
)
2
w^*,b^*=arg\ \underset{w,b}{\min}\sum_{n=1}^{10}{\left( \hat{y}_n-\left( b+wx_n \right) \right) ^2}
w?,b?=arg?w,bmin?n=1∑10?(y^?n??(b+wxn?))2
$$
$$
怎么实现这一过程呢,我们用到的技巧就是Gradient Descent,即梯度下降。
我们先假设考虑w一个参数,假设要求一个w使得上述损失函数最小,我们可以这样干:
步骤1:随机选取一个w0
步骤2:对该点求微分:
? 若微分>0:则使w0减少,得到w1
? 若微分<0:则使w0增加,得到w1
步骤3:根据学习率移动,并重复2,3步,直到loss function取值最低。
如果你觉得抽象,不要担心,来,上图:
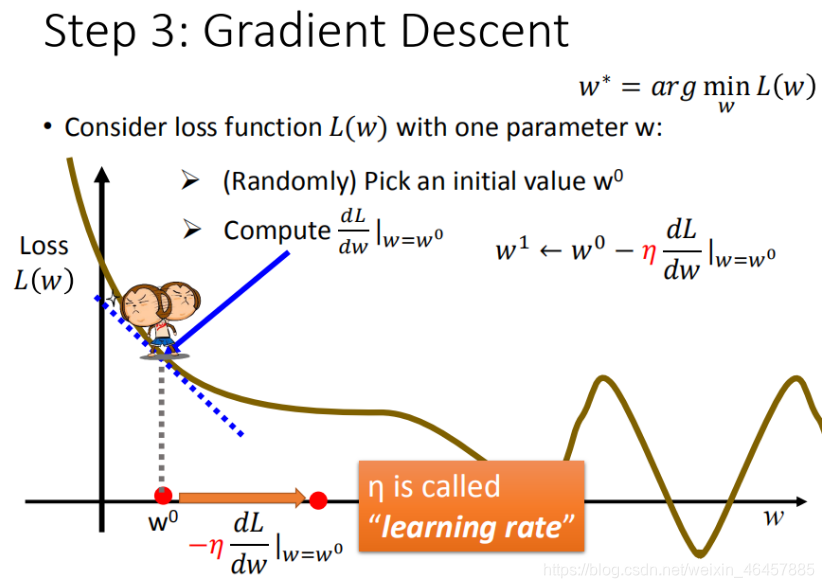
根据上述步骤,我们可以将每一次w的求法量化如下:
w
1
=
w
0
?
η
d
L
d
w
∣
w
=
w
0
w_1=w_0-\eta \frac{dL}{dw}\mid_{w=w_0}^{}
w1?=w0??ηdwdL?∣w=w0??
w 2 = w 1 ? η d L d w ∣ w = w 1 w_2=w_1-\eta \frac{dL}{dw}\mid_{w=w_1}^{} w2?=w1??ηdwdL?∣w=w1??
以此类推,把每一次求得的新的w代入损失函数,直到损失函数最小。
上面的式子中引入了一个常量
η
\eta
η
我们称之为学习率。
从上述式子可以直观感受到,每一个新的w都是在上一个w的基础上移动得到的,而反应这个移动的“步长”,也就是到底移动多少步,我们就可以用这个学习率来描述。
举个例子说,假设我们现在求得某点处的微分>0,则说明该点在loss function的上升段,我们希望找到loss function的最小值,则w一定是最小值点,所以我们希望下一个参与迭代的w要“往后退”,不要再继续往上爬了,于是我们要使该w减少。
同理,如果我们求得该点处微分<0,说明该点处在loss function的下降处,我们希望找到最小值点,当然要让下一个w继续往前走,所以我们让w增加。以上解释也能说明,为什么学习率的系数是负的。
**如果对于w,b都不确定的情况呢?**处理方法也是一样的,无非求的就是偏微分。

比如上图所示。
这里我们会面临一个问题,就是当我们找到最小值时,这个最小值不一定是全局最小,而可能是局部最小,这里我们后面说明。
将上图的偏微分操作整理成一个更简洁的形式,即:
?
L
=
[
?
L
?
w
?
L
?
b
]
g
r
a
d
i
e
n
t
\nabla L=\left[ \begin{array}{c} \frac{\partial L}{\partial w}\\ \frac{\partial L}{\partial b}\\ \end{array} \right] _{gradient}
?L=[?w?L??b?L??]gradient?
上述梯度下降的直观可视化如下:
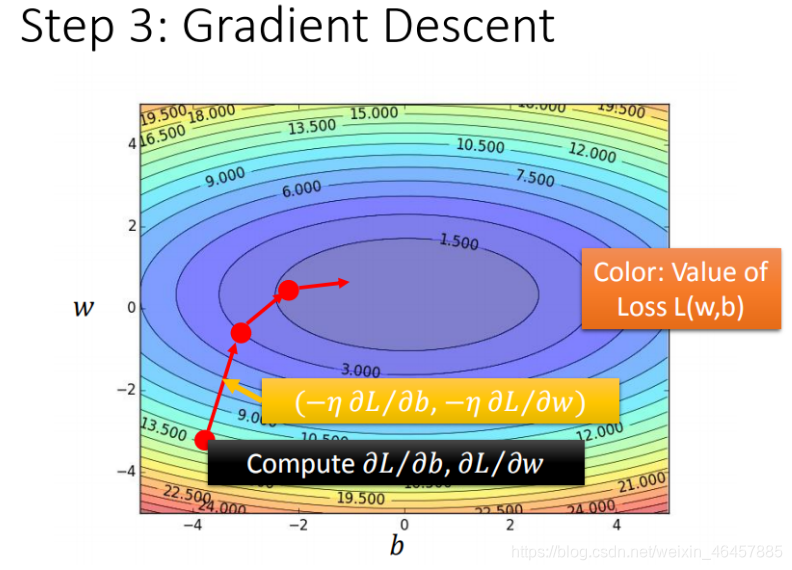
每一圈的线相当于地理学中的等高线,代表损失函数的值,颜色越深,损失函数越小
其中红色箭头的方向,就是每一条等高线在该点处的法线方向,我们在求偏微分时,实际上就是在确定这个方向,沿着法线方向迭代找到最低(高)点,一定是最快的。
梯度下降算法在现实世界中的问题:
● 陷入当前最优
● 等于0
● 趋近于0
验证已训练模型的好坏程度
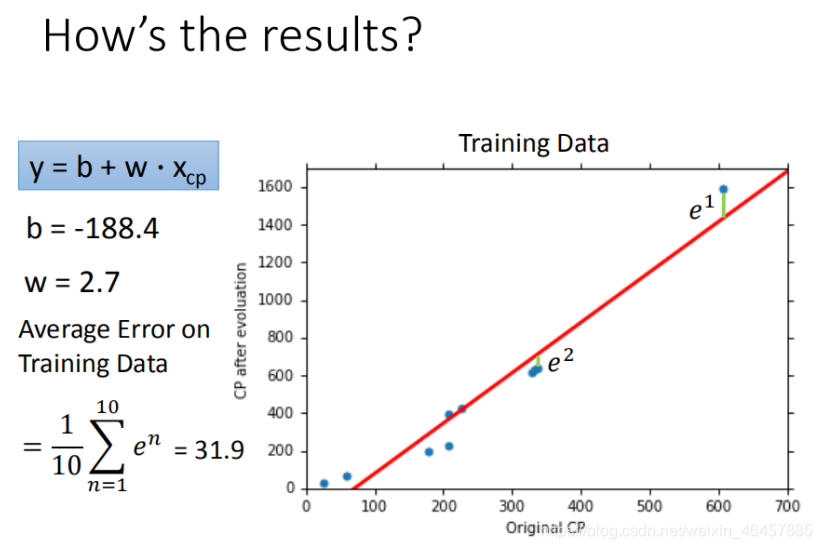
一元高次线性模型
上面我提到的都是一元一次的线性模型,在拟合程度上,局部差距会比较明显,于是我们考虑引入高次方项,即:
y
=
b
+
w
1
x
c
p
+
w
2
x
c
p
2
+
?
+
w
n
x
c
p
n
y=b+w_1x_{cp}+w_2x_{cp}^2+\cdots +w_nx_{cp}^n
y=b+w1?xcp?+w2?xcp2?+?+wn?xcpn?
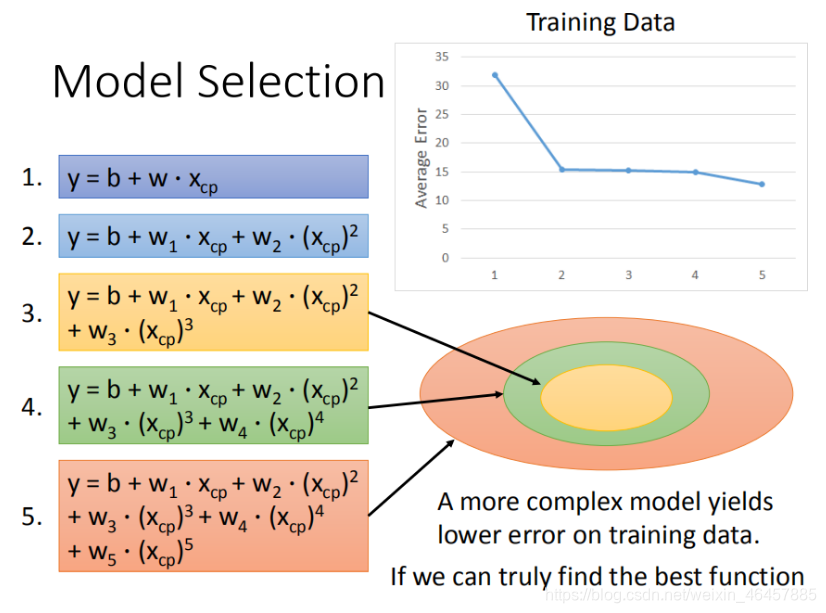
理论上来说,随着最高次方数的增加,平均误差Average Error也会下降,但并不意味着次方数越高模型就越好,还需谨慎过拟合现象,如下图所示:

可以看出,从3次方之后开始,就已经出现了过拟合现象,因此选择模型应该根据实际需求与精度来确定。
优化:多特征模型
● 引入多物种
上述模型中,我们只考虑了精灵现阶段下的CP值,据此预测进化后的CP值。在实际问题中,这样处理欠妥,CP值的确定有可能由多个特征所决定,比如物种。
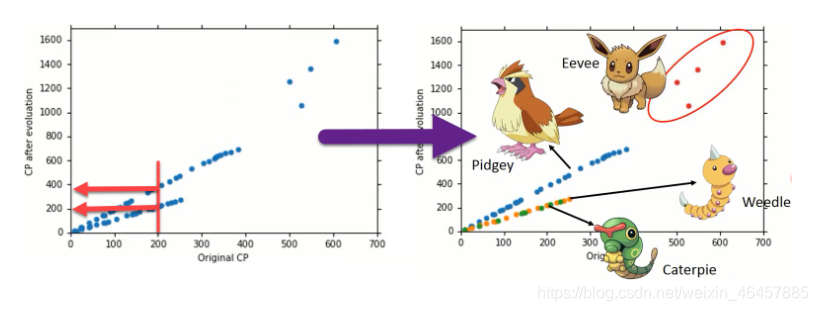
上图显示了四个宝可梦物种的CP值预测模型,可以看出不同物种的回归方程是不同的,我们接下来考虑将上述4个模型,统一到一个模型中去。
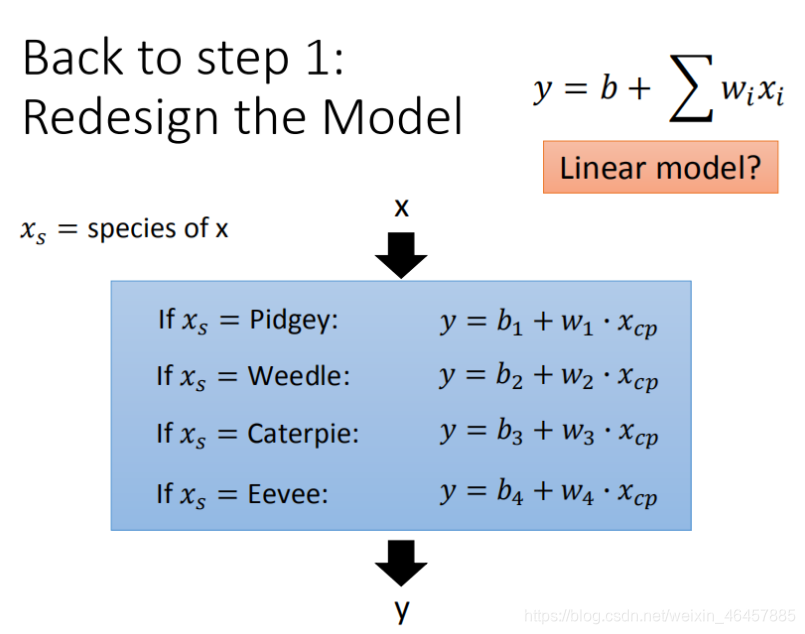
比如像这样:
y
=
δ
1
(
b
1
+
w
1
x
1
)
+
δ
2
(
b
2
+
w
2
x
2
)
+
δ
3
(
b
3
+
w
3
x
3
)
+
δ
4
(
b
4
+
w
4
x
4
)
y=\delta _1\left( b_1+w_1x_1 \right) +\delta _2\left( b_2+w_2x_2 \right) +\delta _3\left( b_3+w_3x_3 \right) +\delta _4\left( b_4+w_4x_4 \right)
y=δ1?(b1?+w1?x1?)+δ2?(b2?+w2?x2?)+δ3?(b3?+w3?x3?)+δ4?(b4?+w4?x4?)
其中我们定义:
δ
1
=
{
1
物种是
P
i
d
g
e
y
0
其他
\delta _1=\begin{cases} 1& \text{物种是}Pidgey\\ 0& \text{其他}\\ \end{cases}
δ1?={10?物种是Pidgey其他?
其他几个常数同理。
● 引入更多参数
比如这样:
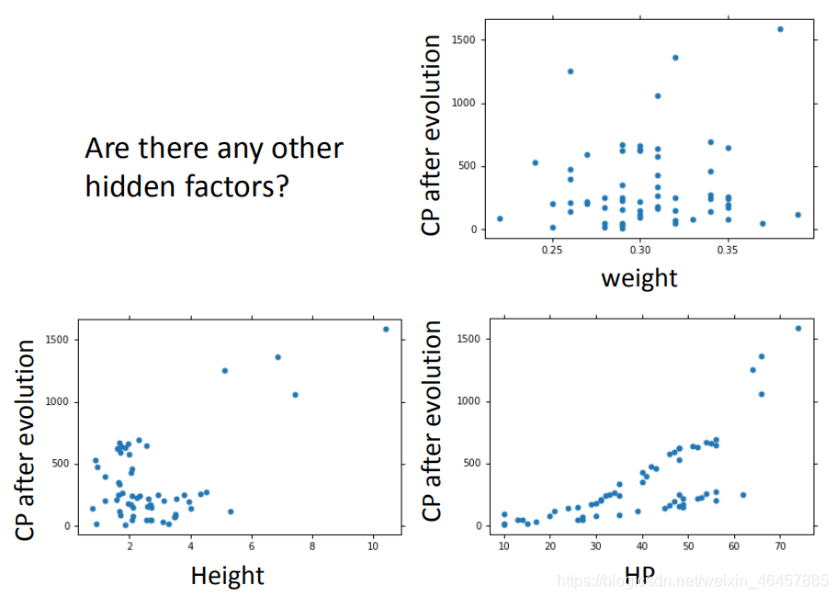
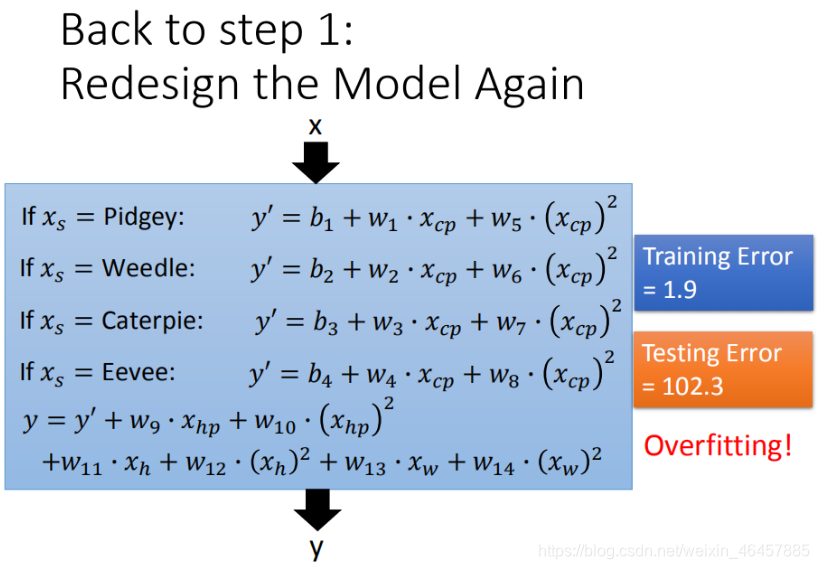
● 引入正则化(Regularization)
所谓引入正则化,即在损失函数中引入某些项,来防止最终求得的模型过拟合的一种手段。
我们回到之前的loss function,在后面更新一项:
L
=
∑
n
(
y
^
n
?
(
b
+
w
i
x
i
)
)
2
+
λ
∑
w
i
2
L=\sum_n^{}{\left( \hat{y}_n-\left( b+w_ix_i \right) \right) ^2}+\lambda \sum{w_i^2}
L=n∑?(y^?n??(b+wi?xi?))2+λ∑wi2?
我们的目的是人工控制那个入的取值,使得最终的w越小越好,这样所求得的模型函数越平滑,平滑即意味着对一些误差的改变不敏感。
如下图所示:
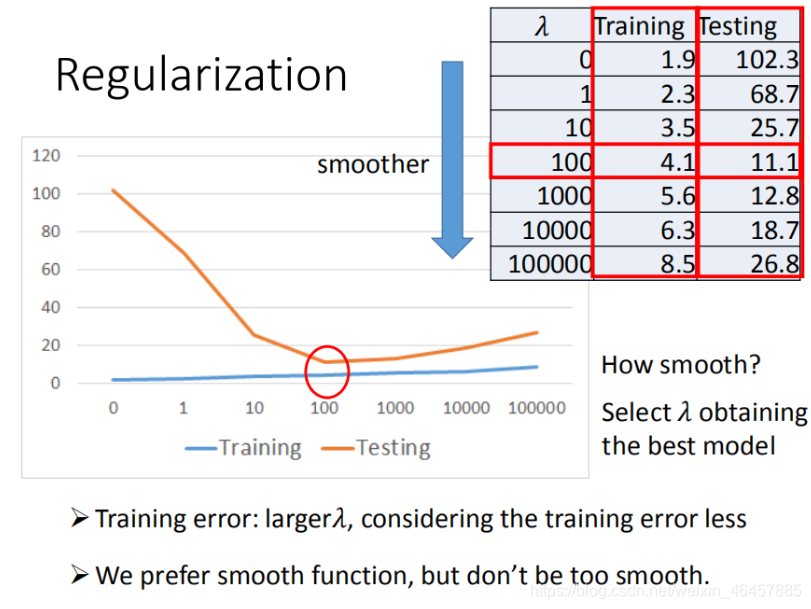
但请注意并非越平滑越好,适当的才是最好的。。。
关于正则化的具体解析日后有机会定会再出一篇来详细讲解,这次先泛泛而谈一下啦~~