回归
回归的应用:
- 股票市场预测——预测明天的道琼斯工业指数
- 自动驾驶汽车——input:censor看到的
? output:方向盘的角度(scalar)
- 推荐系统——找一个function
input:使用者A? 商品B
output:使用者A购买商品B的可能性???
预测宝可梦的CP值(战斗力)
找一个function :
输入是某一只宝可梦相关的信息? 输出就是宝可梦的进化后CP值
输入信息包括:种类、生命值、进化前cp值、重量、高度
Step 1:model
公式:y=b+w·Xcp?? (w 和 b是可以取不同值的参数)
xi是输入的特征值,叫做feature
b:bias?? w:weight
Step 2: goodness of function
收集10只宝可梦的数据
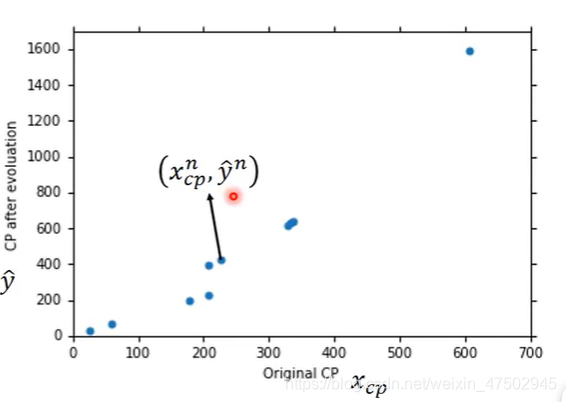
上图中的点表示
横坐标:第n只(上标表示)宝可梦的进化前的cp值
纵坐标:第n只宝可梦进化后的cp值
?
有训练集后就可以定义function的好坏
需要定义一个loss function 记作L
Input:function? output:function有多不好
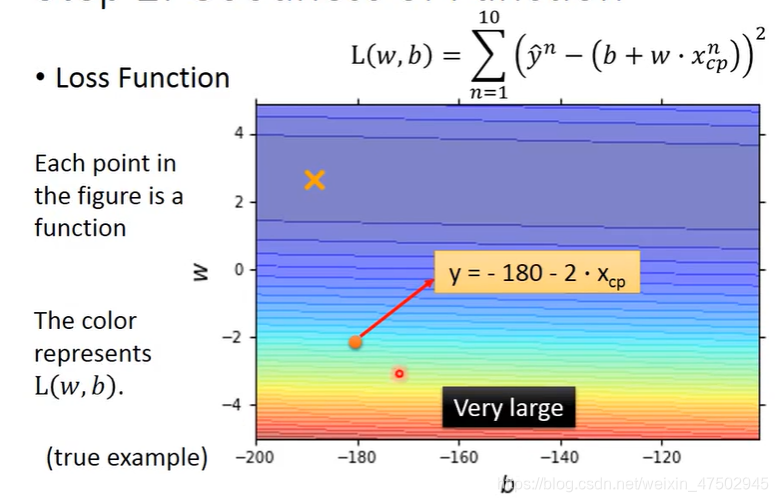
L(f)=L(w,b)在衡量一组参数w b的好坏

真正的数值yhat 减掉用这组参数(w,b)预测出来的预测值y
对这个差值取平方,并计算这10只宝可梦的数据误差合起来
就得到这个function的误差
 ?
?
越偏红色 function越不好
越偏蓝色 function越好?
Step 3 :best function
穷举所有的w和b使loss function 最小

上述方程可以用线代知识来解或使用梯度下降的方法
Gradient descent(梯度下降):
只要L是可微分,都可以用Gradient descent来处理function
具体步骤:
假设当loss function? L(w)中只要一个参数w
找一个w使L最小,可使用暴力穷举的办法
Gradient descent的做法:
1、先随机选取初始的点w0
2、在初始的w0的位置,计算参数w对L的微分,
???? 得出微分为负,增加w的值
???? 得出微分为正,减少w的值
???? 据此调整下一步w的值
3、调整w的幅度大小由上一步的微分值和学习率(learning rate)η有关
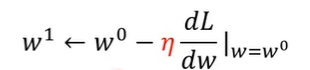
微分结果是负的据上述论证要增加w的值,是正的就要减少w的值
因此增加/减少的值前面有个负号
4、经过t次更新,微分值是0,就没办法继续,此时得到一个局部最小值
但有可能局部最小值不是全局最小值

由于在线性回归中是没有局部最小值的,不会出现上述情况
由一个参数推广到两个参数
1、随机选取初始值w0和b0
分别求w在w0和b在b0对函数L的偏微分
2、分别更新两个参数,并将上述步骤反复
?
最后能找个一个loss比较小的L(w,b)
两个参数的时候是否也会遇到局部最小不是整体最小的问题呢
?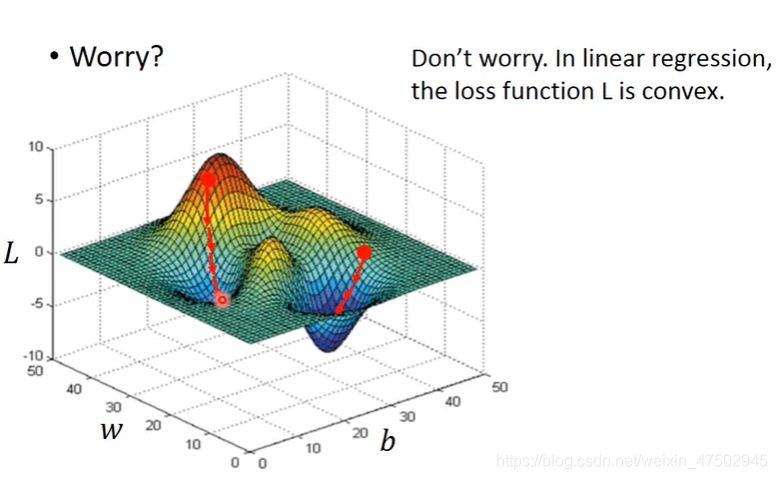
不会:因为线性回归loss function的图像是凸的
(等高线是一圈一圈的)
改进:
重新选取更复杂的模型,
选取二次函数模型、三次函数模型、四次函数模型、五次函数模型
?
模型选取:
模型变得复杂,在训练集上的效果会好,但在测试集上的效果会变差
五次模型可以包含2、3、4次模型
function越复杂,理论上来说可以找到一个function使 error 变低
在testing data上,模型越复杂,不一定能给出好结果,可能会出现overfitting
所以要选择最适合的模型,平衡在训练集和测试集上的错误率
?
重新设计模型:
针对不同的物种,使用不同的function
也能写成函数形式,使用δ函数,能使上述设计用线性函数表达出来
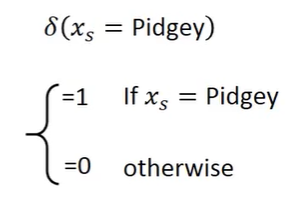
检验下来,在训练集还有测试集都有较好的结果
Regularization 正则化
原来的loss function只考虑了error
现让loss function加上 λ*所有的wi^2的和
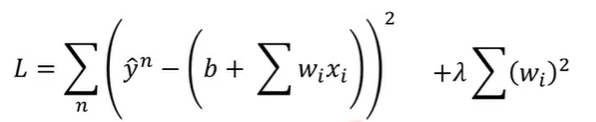
?
期待参数值w越接近0
有更小w的function更好,因为这种function比较平滑,即output对input的变化不敏感,平滑的function对杂项比较不敏感因此受杂项的影响也比较小
在loss function中 λ值越大,考虑error越少,反而越关注w本来的值,找到的function越平滑
我们喜欢比较平滑的function,但也不用太平滑的function,水平的function无意义。
因此就需要调整λ,来使testing error最小
参数b与function的平滑程度无关,因此不用考虑参数b
总结:
1、宝可梦自身的属性包括进化前的cp值等信息对于预测进化后的cp值有重要作用
2、Gradient descent?? 原理和操作步骤
3、过拟合与正则化
4、案例最终得到的testing error平均值约为11.1,在实际情况中是高于/低于预测的平均值?可能会得到更高的error
下节课validation的观念来回答这一问题
视频P4实现代码
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
x_data=[338.,333.,328.,207.,226.,25.,179.,60.,208.,606.]
y_data=[640.,633.,619.,393.,428.,27.,193.,66.,226.,1591.]
#ydata=b+w*xdata
x=np.arange(-200,-100,1)#bias
y=np.arange(-5,5,0.1)#weight
z=np.zeros((len(x),len(y)))
X,Y=np.meshgrid(x,y)
for i in range(len(x)):
??? for j in range(len(y)):
??????? b=x[i]
??????? w=y[j]
??????? z[i][j]=0
??????? for n in range(len(x_data)):
??????????? z[i][j]=z[i][j]+(y_data[n]-b-w*x_data[n])**2
??????? z[i][j]=z[i][j]/len(x_data)
b=-120 #initial b
w=-4? #initial w
lr=1? #learning rate
iteration=100000
#store initial value for plotting
b_history=[b]
w_history=[w]
#give b and w specific learning rate
lr_b=0
lr_w=0
#iteration
for i in range(iteration):
??? b_grad=0.0
??? w_grad=0.0
??? for n in range(len(x_data)):
??????? b_grad=b_grad-2.0*(y_data[n]-b-w*x_data[n])*1.0
??????? w_grad=w_grad-2.0*(y_data[n]-b-w*x_data[n])*x_data[n]
???
??? lr_b=lr_b + b_grad**2
??? lr_w=lr_w + w_grad**2
???
???
??? #updata parameters.
??? b=b-lr/np.sqrt(lr_b)*b_grad
??? w=w-lr/np.sqrt(lr_w)*w_grad
???
??? #store parameters for? plotting
??? b_history.append(b)
??? w_history.append(w)
???
#plot the figure
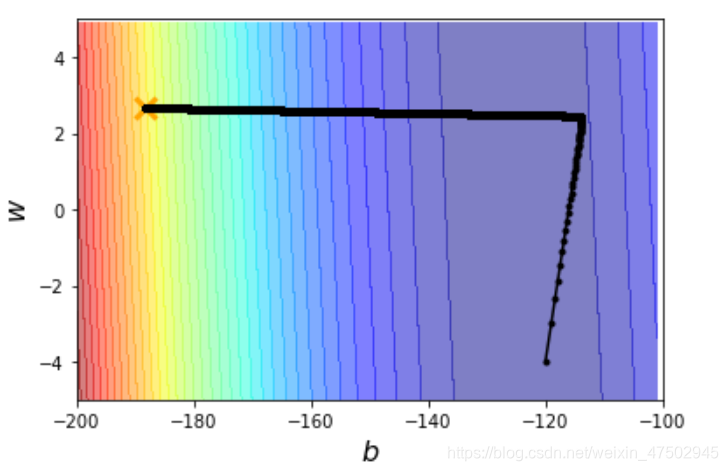
plt.contourf(x,y,z,50,alpha=0.5,cmap=plt.get_cmap('jet'))
plt.plot([-188.4],[2.67],'x',ms=12,markeredgewidth=3,color='orange')
plt.plot(b_history,w_history,'o-',ms=3,lw=1.5,color='black')
plt.xlim(-200,-100)
plt.ylim(-5,5)
plt.xlabel(r'$b$',fontsize=16)
plt.ylabel(r'$w$',fontsize=16)
plt.show()
?
?
图和代码来自李宏毅《机器学习》
https://www.bilibili.com/video/BV1Ht411g7Ef?p=5&spm_id_from=pageDriver
?
?
?
?
?