[人工智能]机器学习基础模型回顾

1 导论

1.1 什么是机器学习？

? 机器学习的一个重要目标就是利用数学模型来理解数据，发现数据中的规律，用作数据分析和预测。

1.1.1 数据？

? 数据通常由一组向量组成，这组向量中的每一个向量都是一个样本，我们用$x_i$来表示一个样本，其中$i=1,2,3...N$，共$N$个样本。每个样本$x_i=\left(x_{i1},x_{i2}...x_{ip},y_i\right)$共$p+1$个维度，$ x_{i1},x_{i2}…x_{ip} $称为特征，$y_{i}$称为因变量或者响应变量。特征用来描述影响因变量$y_{i}$的因素。例如，我们要探寻身高是否会影响体重的关系的时候，身高就是一个特征，体重就是因变量。

? 通常在一个数据表$dataframe$里面，一行表示一个样本$x_i$，一列表示一个特征。

? 对数据形式的约定：

• 第$i$个样本：$x_i={\left(x_{i1},x_{i2}，...，x_{ip},y_i\right)}^T$，$i=1,2,3...N$
• 因变量$y={\left(y_1,y_2，...，y_N\right)}^T$
• 第$k$个特征：$x^{\left(k\right)}={\left(x_{1k},x_{2k},...,x_{Nk}\right)}^T$
• 特征矩阵$X={\left(x_1,x_2，...，x_N\right)}^T$

1.1.2 有监督学习和无监督学习

? 根据数据是否有因变量，机器学习的任务可分为：有监督学习和无监督学习。

• 有监督学习：给定某些特征去估计因变量，即因变量存在的时候，我们称这个机器学习任务为有监督学习。例如，我们用房间面积、房屋所在地区、环境等级等因素去预测某个地区的房价。

  根据因变量是否连续，有监督学习分为回归和分类。

  回归

  分类

  有监督学习

  因变量y是连续型变量 如房价体重

  因变量y是离散型变量 如西瓜是好瓜还是坏瓜

• 无监督学习：给定某些特征，但不给定因变量。建模的目的是学习数据本身的结构和关系。例如，我们给定某电商用户的基本信息和消费记录，通过观察数据中的哪些类型的用户 彼此间的行为和属性类似，形成一个客群。注意，我们本身并不知道哪个用户属于哪个客群，即没有给定因变量。

2 使用sklearn构建完成的机器学习项目流程

? 一般来说，一个完整的机器学习项目分为以下步骤：

? （1）明确项目任务：回归/分类

? （2） 收集数据集并选择合适的特征

? （3） 选择度量模型性能的指标

? （4） 选择具体的模型并进行训练以优化模型

? （5）评估模型的性能并调参

2.1 使用sklearn构建完整的回归项目

（1） 回归问题

（2） 收集数据集并选择合适的特征：

? 我们使用Boston房价数据集的原因：

（3） 选择度量模型性能的指标：

? MSE均方误差：$MSE\left(y,\hat{y}\right)=\frac{1}{n_{samples}}{\sum }_{i=0}^{n_{samples?1}}{\left(y_i?\widehat{y_i}\right)}^2$
? MAE平均绝对误差：$MAE\left(y,\hat{y}\right)=\frac{1}{n_{samples}}{\sum }_{i=0}^{n_{samples?1}}\left|y_i?\widehat{y_i}\right|$

? $R^2$决定系数：$R^2\left(y,\hat{y}\right)=1?\frac{{\sum }_{i=1}^n{\left(y_i?\widehat{y_i}\right)}^2}{{\sum }_{i=1}^n{\left(y_i?\bar{y}\right)}^2}$

? 解释方差得分： E x p l a i n e d V a r i a n c e ( y , y ^ ) = 1 ? V a r { y ? y ^ } V a r { y } ExplainedVariance\left ( y,\hat{y} \right ) = 1 - \frac{Var\left \{ y-\hat{y} \right \}}{Var\left \{ y \right \}} ExplainedVariance(y,y^?)=1?Var{y}Var{y?y^?}?

（4）选择具体的模型并进行训练

? 回归分析时一种预测性的建模技术，它研究的是因变量(目标)和自变量(特征)之间的关系。这种技术通常用于预测分析，时间序列模型以及发现变量之间的因果关系。通常使用曲线/线来拟合数据点，目标是使曲线到数据点的距离差异最小。

线性回归模型：

? 线性回归是回归问题的一种，线性回归假设目标值与特征之间线性相关，即满足一个多元一次方程。通过构建损失函数，来求解损失函数最小时的参数w。

数据集：

D = { ( x 1 , y 1 ) , . . . , ( x N , y N ) } , x i ? R p , y i ? R , i = 1 , 2 , . . . , N D = \left \{ \left ( x_{1},y_{1} \right ),..., \left ( x_{N},y_{N} \right ) \right \} , x_{i}\epsilon R^{p}, y_{i} \epsilon R,i = 1,2,...,N D={(x1?,y1?),...,(xN?,yN?)},xi??Rp,yi??R,i=1,2,...,N

$X={\left(x_1,x_2,...,x_N\right)}^T$

$Y={\left(y_1,y_2,...,y_N\right)}^T$

? 假设X和Y之间存在线性关系，模型的具体形式为：$\hat{y}=f\left(w\right)=w^{T}x$，行向量x列向量=值，所以预测值y往往是一个数字。

最小二乘估计：

? 我们需要衡量真实值$y_i$与线性回归模型的预测值$w^{T}x$之间的差距，在这里我们使用二范数的平方和L(w)来描述这种差距：

$L(w)={\sum }_i^N{\Vert w^T{x}_i?y_i\Vert }_2^2$
$={\sum }_i^N{\left(w^T{x}_i?y_i\right)}^2$
$=\left(w^T{X}^T?Y^T\right){\left(w^T{X}^T?Y^T\right)}^T$
$=w^T{X}^{T}Xw?2w^T{X}^{T}Y+Y{Y}^T$

Tips：为什么平方和不用绝对值？因为绝对值没法求导。

因此，我们需要找到$L(w)$最小时对应的参数$w$，即：$\hat{w}=argminL(w)$，即转化为求解最小化$L(w)$的问题。

求导

令：$\frac{?L(w)}{?w}$$=2X^{T}Xw?2X^{T}Y$$=0$

因此：$\hat{w}={\left(X^{T}X\right)}^{?1}{X}^{T}Y$

几何解释：

? 向量a和向量b互相垂直，则$?a,b?=a^{T}b=0$

? 平面X的法向量$Y?Xw$与平面$X$互相垂直，因此$X^T(Y?Xw)=0$，即：$\hat{w}={\left(X^{T}X\right)}^{?1}{X}^{T}Y$

? [外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-bkeY4lgo-1626358562996)(C:\Users\DELL-PC\AppData\Roaming\Typora\typora-user-images\image-20210715204737292.png)]

概率视角：

3 作业

3.1 请详细阐述线性回归模型的最小二乘法表达。

最小二乘估计：

? 我们需要衡量真实值$y_i$与线性回归模型的预测值$w^{T}x$之间的差距，在这里我们使用二范数的平方和L(w)来描述这种差距：

$L(w)={\sum }_i^N{\Vert w^T{x}_i?y_i\Vert }_2^2$
$={\sum }_i^N{\left(w^T{x}_i?y_i\right)}^2$
$=\left(w^T{X}^T?Y^T\right){\left(w^T{X}^T?Y^T\right)}^T$
$=w^T{X}^{T}Xw?2w^T{X}^{T}Y+Y{Y}^T$

Tips：为什么平方和不用绝对值？因为绝对值没法求导。

因此，我们需要找到$L(w)$最小时对应的参数$w$，即：$\hat{w}=argminL(w)$，即转化为求解最小化$L(w)$的问题。

求导

令：$\frac{?L(w)}{?w}$$=2X^{T}Xw?2X^{T}Y$$=0$

因此：$\hat{w}={\left(X^{T}X\right)}^{?1}{X}^{T}Y$

3.2 在线性回归模型中，极大似然估计与最小二乘估计有什么联系和区别？

(12条消息) 最大似然估计和最小二乘估计的区别与联系_梦想腾飞-CSDN博客_极大似然估计和最小二乘估计的区别

(12条消息) 最大似然估计(MLE)与最小二乘估计(LSE)的区别_你若盛开，清风自来-CSDN博客

3.3 为什么多项式回归在实际问题中的表现经常不是很好？

? 当阶数越高，多项式的曲线越光滑，在数据点较少的边界波动较大，边界数据的预测精确度较低。

3.4 决策树模型与线性模型之间的联系与区别？

3.5 什么是KKT条件？

KKT(最优解的一阶必要条件)

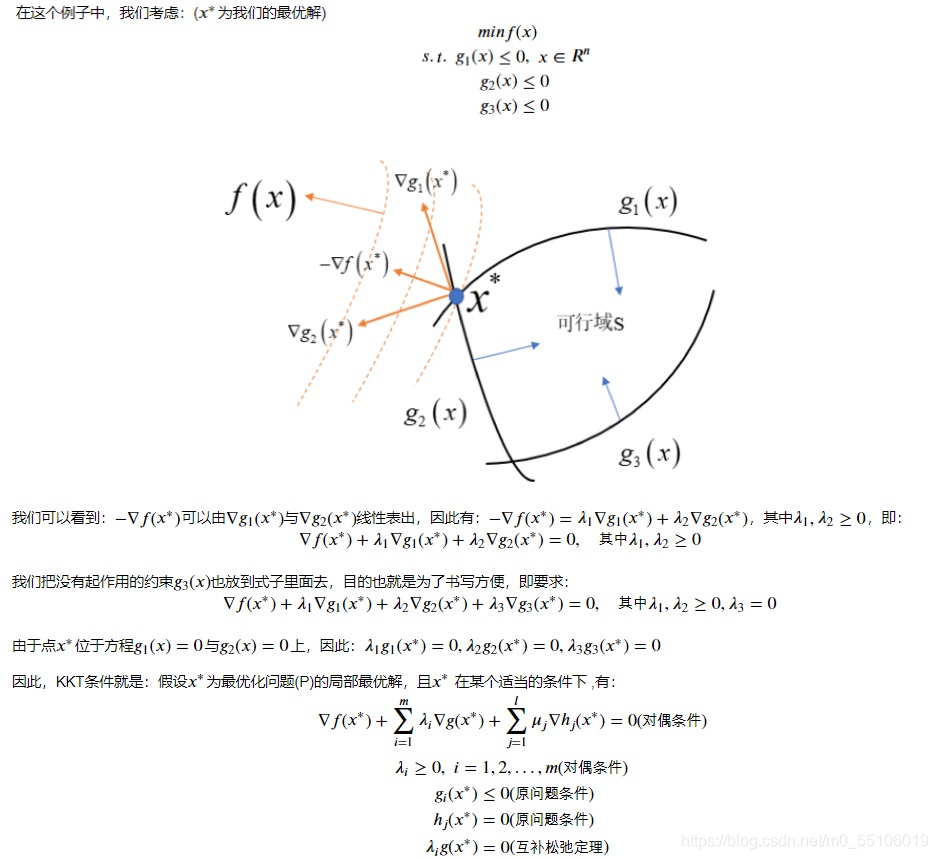
3.6 为什么要引入原问题的对偶问题？

? 因为原问题与对偶问题就像是一个问题两个角度去看，如利润最大与成本最低等。有时侯原问题上难以解决，但是在对偶问题上就会变得很简单。再者，任何一个原问题在变成对偶问题后都会变成一个凸优化的问题，

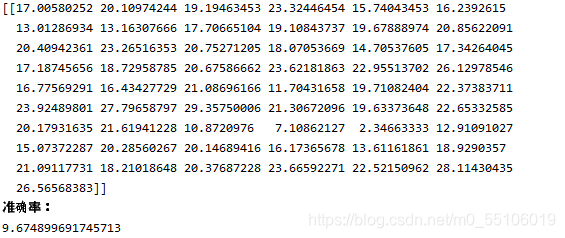
3.7 使用CH1机器学习数学基础所学的内容，找到一个具体的数据集，使用线性回归模型拟合模型，要求不能使用sklearn，只能使用python和numpy。

波士顿房价预测

def openFileAndSplit():
    # 打开并且分割字符

    with open(r"F:\housing_data.txt", 'r') as f:

        for line in f.readlines():
            b = []
            for x in line.split():
                b.append(float(x))
            a.append(b)
            
def duoyuanxianxinghuigui():
    # 多元线性回归模型
    b = []
    # 分离最后一列
    for l in a:
        b.append([l.pop()])
        l.append(1)
    a1 = np.mat(a[0:449])
    a2 = np.mat(a[450:505])
    b1 = np.mat(b[0:449])
    b2 = np.mat(b[450:505])
    k = np.matmul(a1.transpose(1, 0), a1).I
    k = np.matmul(np.matmul(k, a1.transpose(1, 0)), b1)
    ans = np.matmul(a2, k).transpose(1, 0)
    # 均方差计算准确率
    accuRate = np.array(ans - b2.transpose(1, 0))[0]
    print(ans)
    print("准确率：")
    print(sum(accuRate * accuRate) / len(accuRate))


def main():
    openFileAndSplit()
    duoyuanxianxinghuigui()


main()