机器学习基本概念简介:
- 机器学习模型中的两类参数:
- 模型参数(Parameter):
- 需要从数据中学习和估计得到,称为模型参数(Parameter)—即模型本身的参数。比如,线性回归直线的加权系数(斜率)及其偏差项(截距)都是模型参数.
- 超参数(hyperparameter):
- 机器学习算法中的调优参数(tuning parameters),需要人为设定,称为超参数(Hyperparameter)。比如,正则化系数λ,决策树模型中树的深度,梯度下降法中的学习速率α,迭代次数epoch,批量大小batch-size,k近邻法中的k(最相近的点的个数),决策树模型中树的深度,等等
- 模型参数(Parameter):
机器学习寻找函数的过程:
-
写出一个带有未知参数的函数:
- 比如,可以先写出 y=f(x)或是y=b+wx1
- model:y=b+wx1
- weight:w
- bias:b
-
定义一个loss:
- Loss: L=1/n(e1+e2+…+en)
- mean absolute error(MAE) e=|y-y’|
- mean square error(MSE) e=(y-y’)^2
- question:为什么loss的值会是负的:
- answer:loss是自己设定的,所以有可能会变成复数,比如设置为loss=|y-y‘|-100
-
Optimization:
- 找出使得L最小的一组w和b,记为w ,b**
- 随机选择一个初始的点w0
- 计算L关于w的导数、微分
- 使用梯度下降算法等更新w的值
- 要设置learning rate学习率
- hyperparameters:
- 做机器学习时需要自己设定的东西(参数)
- 找出使得L最小的一组w和b,记为w ,b**
深度学习基本概念简介:
激活函数(Activation Function):
-
Sigmoid:
-
ReLU(Rectified Linear Unit):
- c max(0,b+wx)
- 2个ReLU可以合出一个hard Sigmoid
-
这些Sigmoid或者ReLU叫做Neuron(神经元),很多的Neuron就叫做Neural Network,每一排Neuron叫做Layer(Hidden Layer),很多的Hidden Layer就叫做Deep,这一整套技术就叫做Deep Learning
当training data上的loss函数太大时,可能会有两个原因:
- Model Bias 太小
- Optimization Issue(没有选好优化方式)
当training data上的loss函数太小时:
- 如果testing data上的loss函数也很小就刚好符合要求
- 如果testing data上的loss函数比较大,就可能是发生了overfitting
当optimization时loss一直降不下去的时候:
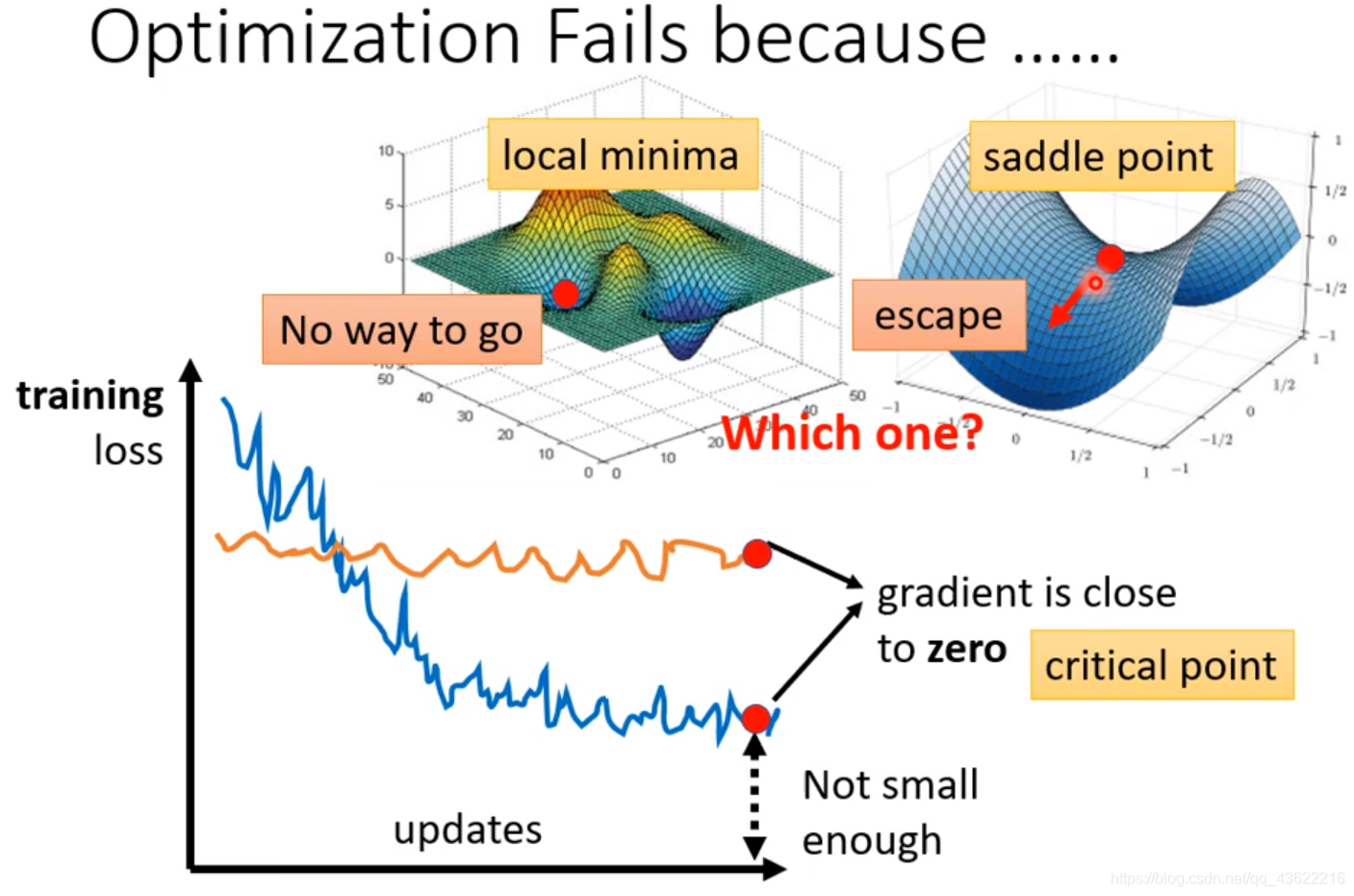
- 可能陷入了local minima
- 可能陷入了 saddle point
- 可能陷入了local maxima
- 这些点的梯度gradient都是0,统称为critical point
那该怎么区分此时是在哪一点呢?
假设此时函数参数位于
θ
\theta
θ,由泰勒级数,我们可以近似地表示出当参数位于
θ
\theta
θ附近的
θ
′
\theta'
θ′时函数的值:
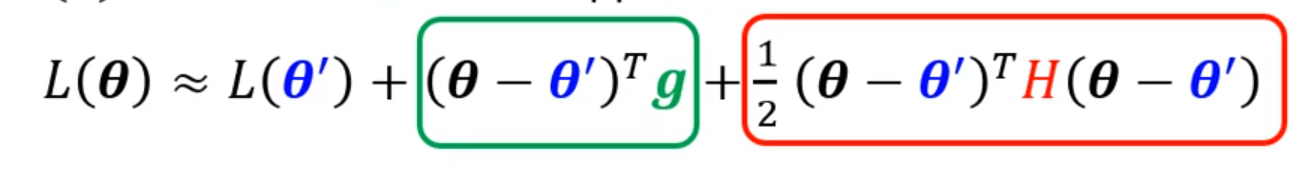
里面的g是函数L在
θ
′
\theta'
θ′处的梯度,是一个向量;里面的H表示一个Hessian Matrix,可以将其理解为在点
θ
′
\theta'
θ′处的二阶导数: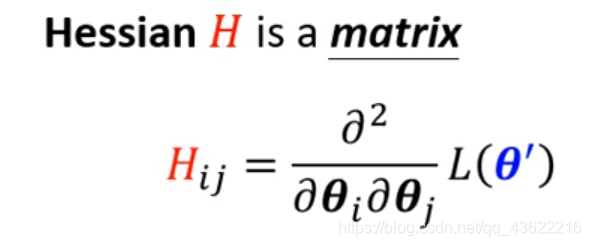
由于函数陷入的一点梯度为0,所以我们可以只关注后面的一项,式子可以表示为:
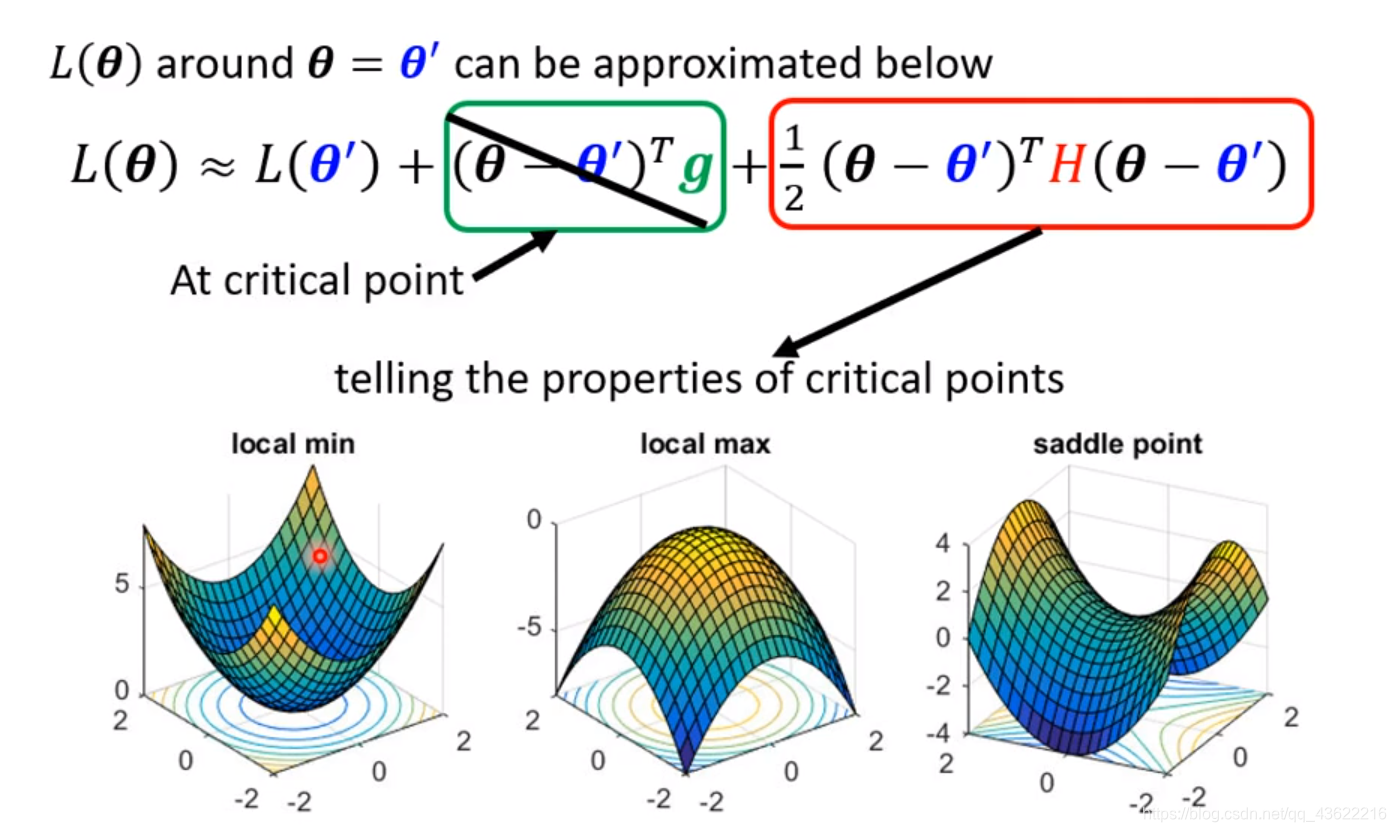
此时,我们将
(
θ
?
θ
′
)
(\theta-\theta')
(θ?θ′)表示为v,可以得到下图这三种情况:
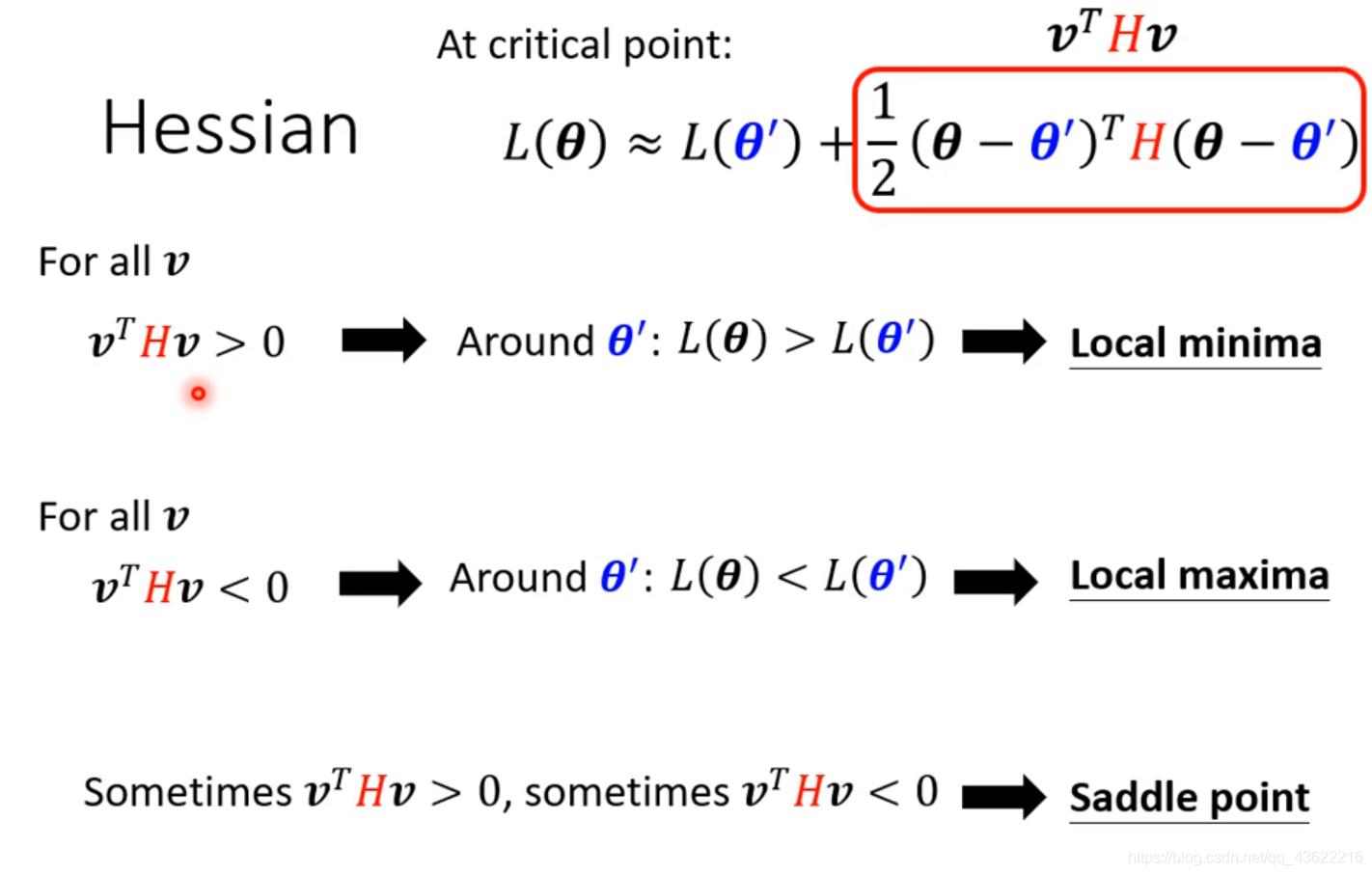
- 对于 θ ′ \theta' θ′附近的所有 θ \theta θ,都有 v T H v > 0 v^THv>0 vTHv>0,也即矩阵H是一个正定矩阵:说明在 θ \theta θ点上,函数L的值等于在点 θ ′ \theta' θ′处的函数值加上一个正数,这个结果都会比在点 θ ′ \theta' θ′处的值要大,即点 θ ′ \theta' θ′是一个极小值点,Local minima
- 对于 θ ′ \theta' θ′附近的所有 θ \theta θ,都有 v T H v < 0 v^THv<0 vTHv<0,也即矩阵H是一个负定矩阵:说明在 θ \theta θ点上,函数L的值等于在点 θ ′ \theta' θ′处的函数值加上一个正=负数,这个结果都会比在点 θ ′ \theta' θ′处的值要小,即点 θ ′ \theta' θ′是一个极大值点,Local maxima
- 对于 θ ′ \theta' θ′附近的所有 θ \theta θ,有些 v T H v > 0 v^THv>0 vTHv>0,有些 v T H v < 0 v^THv<0 vTHv<0:由以上两种情况可知,这种情况下在 θ ′ \theta' θ′点周围有些地方高有些地方低,意味着这是一个Saddle point
- 矩阵的正定可以计算特征值或是看各阶主子式是否全大于0,特征值全大于0说明是正定矩阵,小于0说明是负定矩阵;各阶主子式全大于0说明是正定矩阵