?
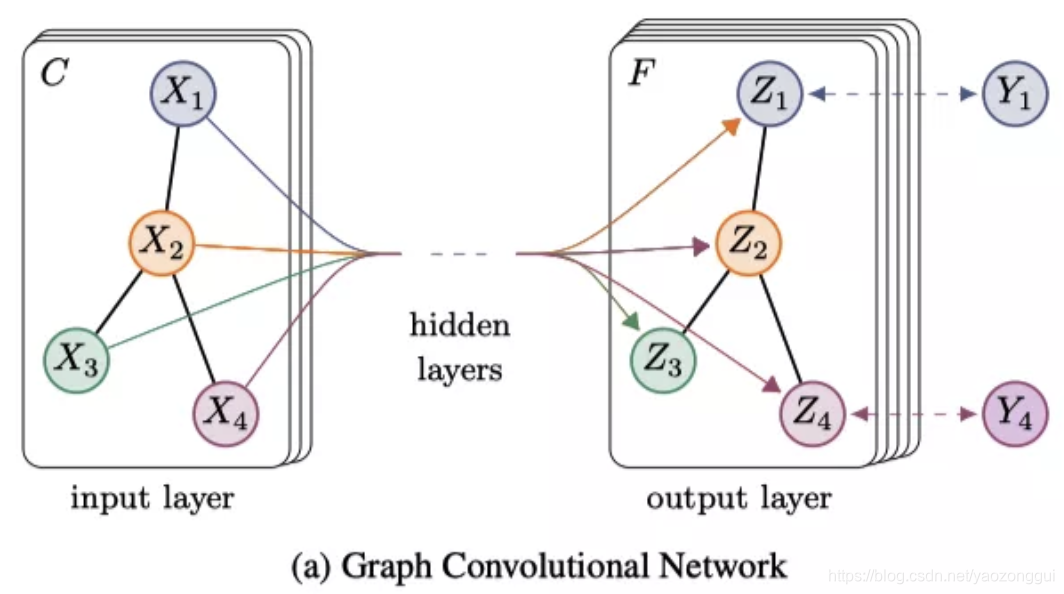
本文主要介绍图卷积神经网络(GCN)的理解要点与梗概。首先需要指明的是,图卷积神经网络(GCN)与图神经网络(GNN)是有区别的。图神经网络(GNN)可以看作在非欧结构数据上进行特征提取的深度神经网络结构的统称,而图卷积网络(GCN)特指能够使用卷积操作对非欧数据进行特征提取的深度神经网络。在图卷积神经网络(GCN)这一分支中,又能够衍生出许多使用了不同方式实现卷积操作的神经网络。本文主要涉及谱(spectral)方法的图卷积神经网络。
对于卷积操作的定义,在图像领域中是基于傅里叶变换,将两个函数进行卷积的。具体地,参考卷积定理的描述,即:两信号在时域的卷积积分对应于在频域中该两信号的傅立叶变换的乘积。对应于如下公式:
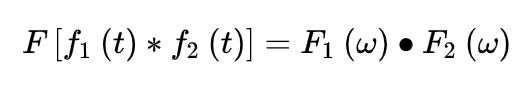
此时我们所涉及的卷积操作是一维卷积操作。进而有卷积公式:
![]() ?
?
自然地,既然在欧氏空间内,卷积操作可以衍变为频域内的乘积操作,那么在非欧空间内,对这种操作进行推广,会达到对空间域信息进行分解,进而进行卷积的目的。这一步的具体数学证明较为晦涩,但总体概念并不难理解。首先需要找到类似傅里叶变换的运算。这种计算就可以使用拉普拉斯算子来实现。这里只说明,拉普拉斯算子能够类比傅里叶展开式中积分的被积函数因子,作为一种类似算法进行使用。实际上,傅里叶分析是拉普拉斯分析的一个特例。由此可以得出,为了进行非欧空间的卷积操作,我们只需要使用拉普拉斯算子对参与卷积的函数进行频域转化,最终即可将空间域的卷积操作转化为频域的乘积操作。
对于一个图而言,拉普拉斯算子的定义为度矩阵(D)减去邻接矩阵(A):
![]()
对于图而言,拉普拉斯算子演化为拉普拉斯矩阵。那么欧氏空间内,对函数进行频域转化,相当于对函数进行如下操作:
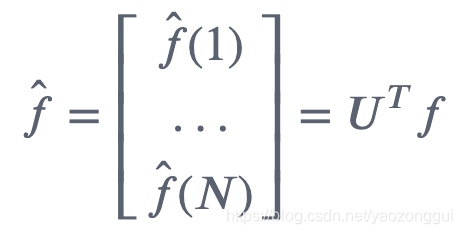
其中,U是拉普拉斯矩阵的特征向量。
如此,就得到非欧空间下的卷积公式:?
![]()
?其中,g?作为卷积核整体看待。这种运算参数计算量庞大(即图节点个数n),后期改进为K阶切比雪夫展开等方法进行计算,可以较大程度减少卷积核的参数,实质上将全图的共同作用力缩减为以节点为中心的第K层作用力,并无需进行特征分解。而神经网络实际中使用的图卷积公式为:
?![]()
首先注意到其中已经省去了特征向量U的计算,其次,?A 为邻接矩阵,I为单位矩阵,D为A相关计算矩阵,目前图卷积网络简化表示为:
![]()
![]()
?从中可见目前使用的图卷积网络基本类比于图节点特征赋予权值W后,再融入图结构信息的稀疏邻接矩阵。我们可以类比全连接网络记忆,即:体现权值与信息连接关系。
本文对于图卷积网络的描述比较浅显,帮助大家进行梗概理解,信息收集过程中参考了很多前辈的工作,另外介绍一篇微信长文:《万字长文带你入门 GCN》,具体公式推导可相应参考。
?
?
?
?