第一次写这个,很多不太懂,希望自己以后把学习的笔记、阅读的文献都记录下来,看到自己不断进步的过程,也和大家互相分享学习、共同探讨知识,加油!
线性模型
进行深度学习时的准备过程
- 准备数据集
- 选择模型
- 模型训练
- 进行推理预测
举例:对于某产品花费x工时,即可收到y效益,有表如下
| x(hours) | y(points) |
|---|---|
| 1 | 2 |
| 2 | 4 |
| 3 | 6 |
| 4 | ? |
求问花费4工时的条件下,可获得收益为多少?
模型设计:y=xw+b 训练模型的过程即确定参数w和b
下图以 y=xw 建模
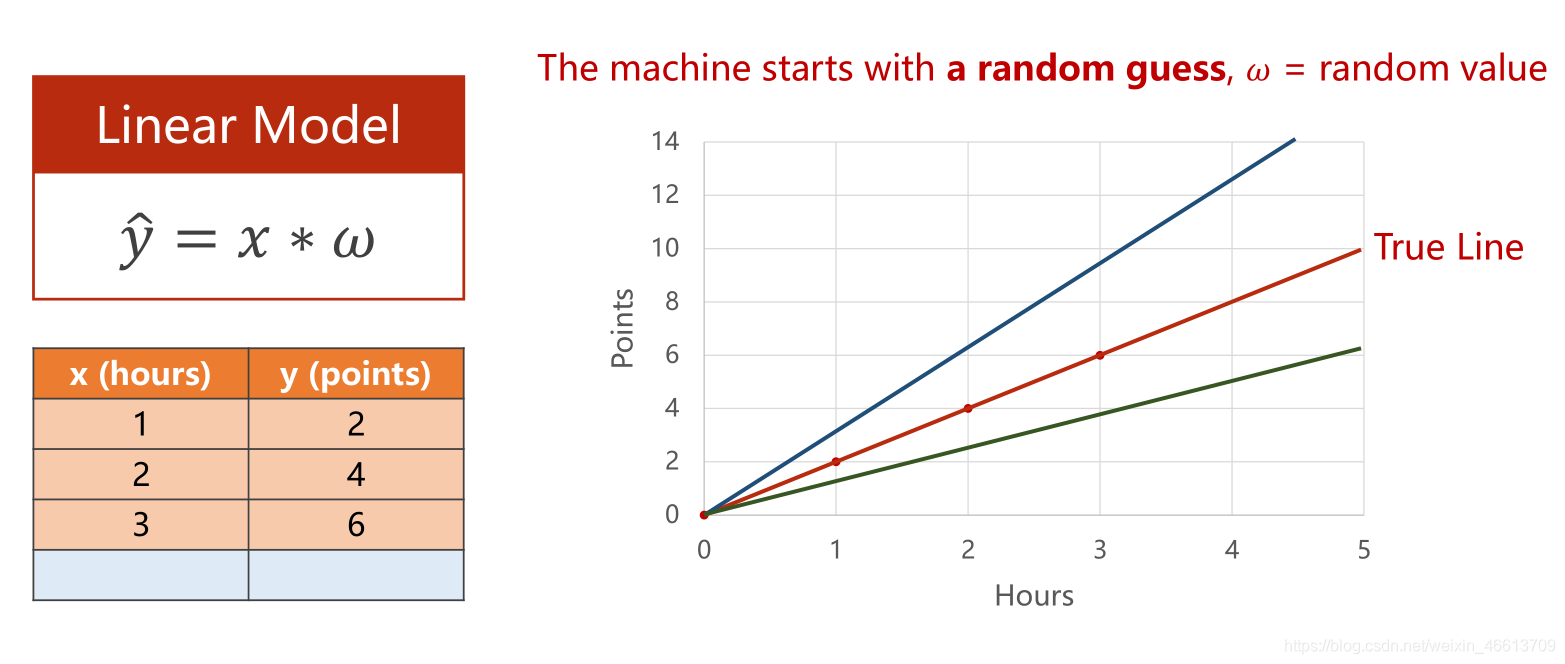
在模型训练中会先随机取得一个值,继而计算其和标准量之间的偏移量,从而判断当前模型是否符合预期。
记实际值为y(x),模型对应的预测值为
y
^
(
x
)
\widehat y(x)
y
?(x),则其中的偏移量为
∣
y
^
(
x
)
?
y
(
x
)
∣
\left|\widehat y(x)-y(x)\right|
∣y
?(x)?y(x)∣,以此来代表模型估计值对原值的误差。
通常,该公式定义为Training Loss (Error)
l
o
s
s
=
(
y
^
?
y
)
2
=
(
ω
x
?
y
)
2
loss = (\widehat y - y)^2 = (\omega x - y)^2
loss=(y
??y)2=(ωx?y)2
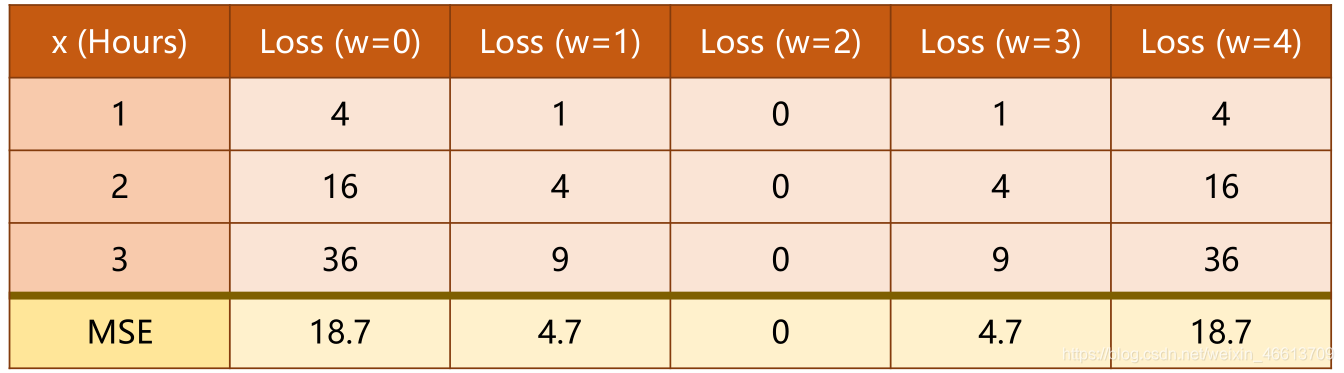
原题目中的几种
ω
\omega
ω所对应的Loss如下
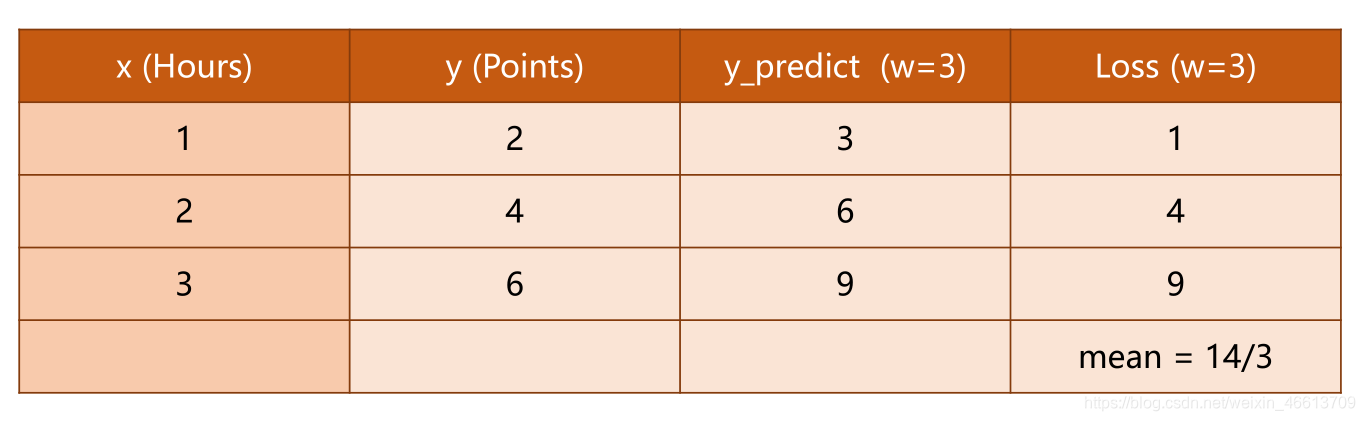
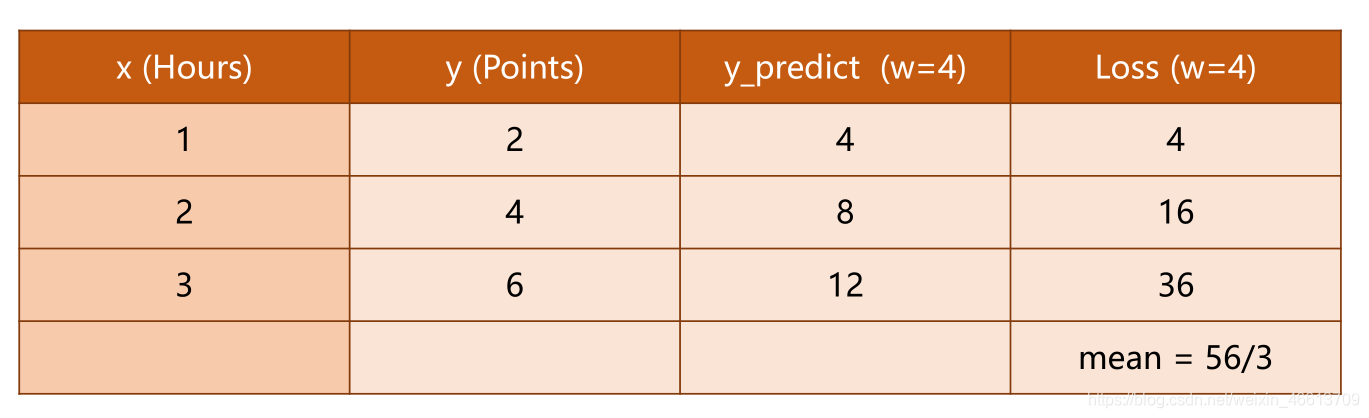
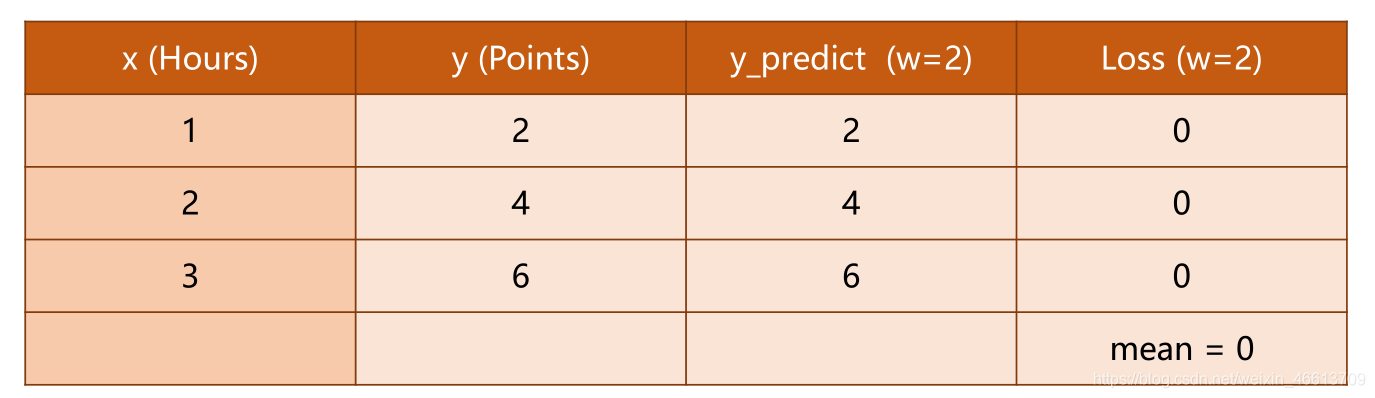
其中的每行为
w
w
w不同时的单个样本的损失,最后一行为平均损失。
对于单个样本,有loss可用于指代样本误差。对于所有样本,可同理用==Mean Square Error (MSE)==来指代整体样本的平均平方误差(均方差cost)
c
o
s
t
=
1
N
∑
n
=
1
N
(
y
^
n
?
y
n
)
2
cost = \frac{1}{N} \displaystyle\sum_{n=1}^{N}(\widehat y_n-y_n)^2
cost=N1?n=1∑N?(y
?n??yn?)2
由cost的计算公式可知,当平均损失为0时,模型最佳,但由于仅当数据无噪声且模型完美贴合数据的情况下才会出现这种情况,因此模型训练的目的应当是尽可能小,而非找到误差为0的情况。
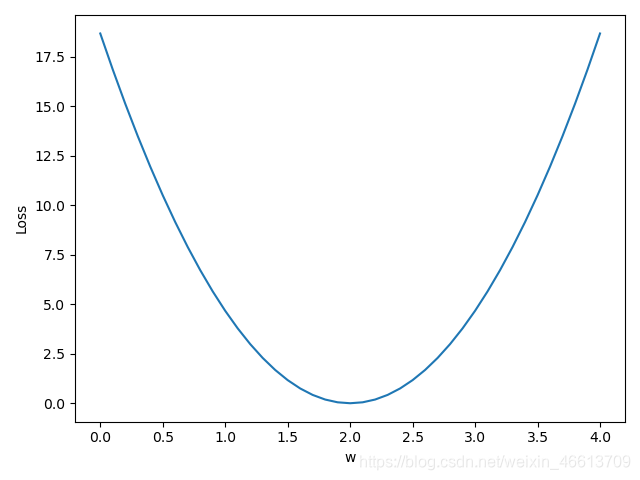
代码及曲线图
import numpy as np
import matplotlib.pyplot as plt
x_data = [1.0, 2.0, 3.0]
y_data = [2.0, 4.0, 6.0]
#前馈计算
def forward(x):
return x * w
#求loss
def loss(x, y):
y_pred = forward(x)
return (y_pred-y)*(y_pred-y)
w_list = []
mse_list = []
#从0.0一直到4.1以0.1为间隔进行w的取样
for w in np.arange(0.0,4.1,0.1):
print("w=", w)
l_sum = 0
for x_val,y_val in zip(x_data,y_data):
y_pred_val = forward(x_val)
loss_val = loss(x_val,y_val)
l_sum += loss_val
print('\t',x_val,y_val,y_pred_val,loss_val)
print("MSE=",l_sum/3)
w_list.append(w)
mse_list.append(l_sum/3)
#绘图
plt.plot(w_list,mse_list)
plt.ylabel("Loss")
plt.xlabel('w')
plt.show()
练习:尝试使用y=x*w+b模型训练,并画出误差函数图像
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
x_data=[1.0,2.0,3.0]
y_data=[2.0,4.0,6.0]
def forward(x,b):
return x * w + b
def loss(x,y,b):
y_pred = forward(x,b)
return (y_pred-y) * (y_pred-y)
w_list=[]
b_list=[]
mse_list=[]
for w in np.arange(0.0,4.1,0.1):#从0.0一直到4.1以0.1为间隔进行w的取样
for b in np.arange(-2.0,2.1,0.1):
print('w=',w)
print('b=',b)
l_sum=0
for x_val,y_val in zip(x_data,y_data):
y_pred_val=forward(x_val,b)
loss_val=loss(x_val,y_val,b)
l_sum+=loss_val
print('\t',x_val,y_val,y_pred_val,loss_val)
mse_list.append(l_sum / 3)
print('MSE=',l_sum/3)
b_list.append(b)
w_list.append(w)
fig=plt.figure()
ax=Axes3D(fig)
x=np.array(w_list)
y=np.arange(-2.0,2.1,0.1)
print(x.shape)
print(y.shape)
z=np.reshape(mse_list,(x.__len__(),y.__len__()))
x,y=np.meshgrid(x,y)
ax.plot_surface(x,y,z)
plt.show()
