前言
PSO-for-Neural-Nets
大家知道,使用反向传播对神经网络进行训练是非常有效的。但如果网络参数的初始值设得不好时,各位可能也有过训练十分缓慢的经历。
这里提供一种加快反向传播的算法,目的是在训练神经网络时不使用反向传播以及梯度下降算法,而是先使用粒子群优化算法(Particle Swarm Optimization,PSO)对网络参数进行初始化,之后可以再次使用反向传播对网络进行正式训练。
1 粒子群优化 PSO
粒子群优化是一种元启发式算法(meta-heuristics algorithm),它属于基于种群的元启发式方法的一个子类。这意味着将多个粒子放置在 n 维解空间中,让其不断移动以获得最优解。对于不熟悉粒子群优化的童鞋,可以网络上找资料快速了解一下。比如这篇,很容易理解。
2 神经网络
前馈神经网络: 前馈神经网络是两个操作(一个线性操作,然后是一个非线性操作)的堆栈,这些操作被多次应用以找出映射 。
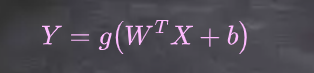

3 将两者结合

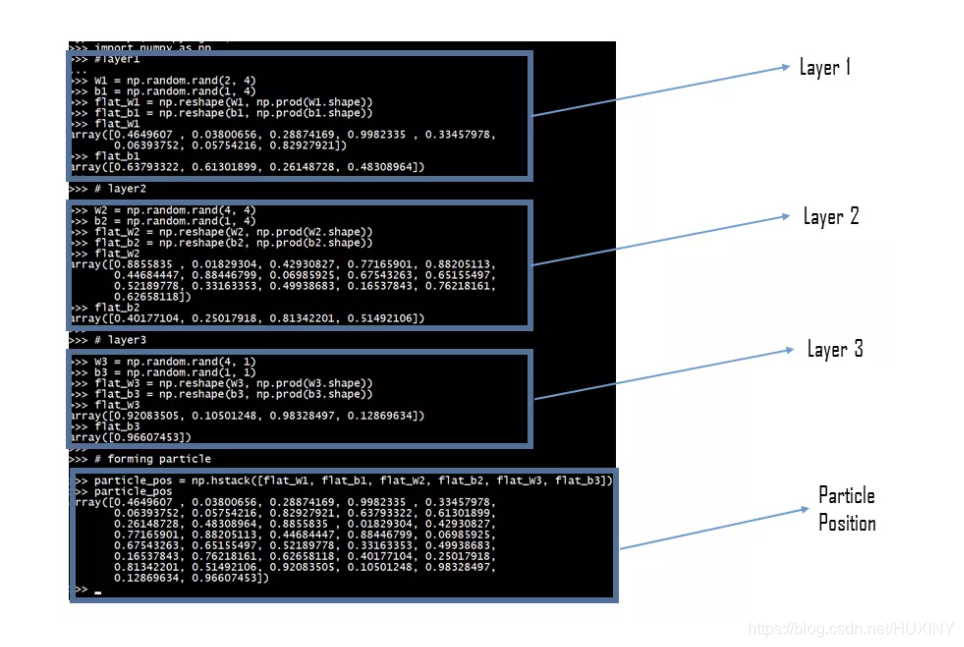
import numpy as np
from swarm_intelligence.particle import Particle
from swarm_intelligence.pso import ParticleSwarmOptimizer
from matplotlib import pyplot as plt
mean_01 = np.array([1.0, 2.0])
mean_02 = np.array([-1.0, 4.0])
cov_01 = np.array([[1.0, 0.9], [0.9, 2.0]])
cov_02 = np.array([[2.0, 0.5], [0.5, 1.0]])
ds_01 = np.random.multivariate_normal(mean_01, cov_01, 250)
ds_02 = np.random.multivariate_normal(mean_02, cov_02, 250)
all_data = np.zeros((500, 3))
all_data[:250, :2] = ds_01
all_data[250:, :2] = ds_02
all_data[250:, -1] = 1
np.random.shuffle(all_data)
split = int(0.8 * all_data.shape[0])
x_train = all_data[:split, :2]
x_test = all_data[split:, :2]
y_train = all_data[:split, -1]
y_test = all_data[split:, -1]
def sigmoid(logit):
return 1 / (1 + np.exp(-logit))
def fitness(w, X=x_train, y=y_train):
logit = w[0] <em> X[:, 0] + w[1] </em> X[:, 1] + w[2]
preds = sigmoid(logit)
return binary_cross_entropy(y, preds)
def binary_cross_entropy(y, y_hat):
left = y * np.log(y_hat + 1e-7)
right = (1 - y) * np.log((1 - y_hat) + 1e-7)
return -np.mean(left + right)
pso = ParticleSwarmOptimizer(Particle, 0.1, 0.3, 30, fitness,
lambda x, y: x<y, n_iter=100,
dims=3, random=True,
position_range=(0, 1), velocity_range=(0, 1))
pso.optimize()
print(pso.gbest, fitness(pso.gbest, x_test, y_test))
26%|██▌ | 26/100 [00:00<00:00, 125.34it/s]
1.1801928375606305
1.4209814927365876
1.6079804335787051
1.4045063665887232
1.6061883358646398
1.216230952537311
1.092492742843725
1.425740352398705
1.2316560685535152
0.9883386170699404
0.7872754467763685
1.2949776923674654
1.5335307808402896
1.4402299491203296
1.707301581201865
1.3663291698028996
0.810679674134304
0.902645267001228
...
0.6887999501032107
0.6888687686160592
0.688937050625055
0.6890767713425439
0.6892273324647994
0.6890875560305971
0.689124619992127
0.6898172338259064
0.6887098887333781
0.6887212601101861
0.688826316853767
0.6892384007287018
0.6844381943050638
0.689115638510458
0.6891453159612045
0.6901587770829556
0.6895998527186173
0.6890967086445332
0.689073485303836
0.6883588252450673
[0.00451265 0.21376644 0.22467216] 0.6875450245414241
粒子群优化算法属于元启发算法的一种,寻优往往需要额外的计算时间。并且,元启发算法对问题的维数相对敏感,运算复杂度会随着问题维数的规模增加很快,不利于像大型复杂神经网络复杂的寻优。
但是对比梯度下降方法,元启发也有很多优势,比如梯度下降也有一些问题,比如对初始条件敏感,如果初始条件好则收敛快,初始条件不好可能就不收敛。所以对于不是十分复杂的网络架构,或许元启发算法可以得到一个比较不错的初始化。