[集成学习]task02:回归问题
- 线性回归模型
求解线性回归模型的参数：
构建一个含有参数的 Loss Function，求解使得 Loss Function最小的参数的值。
一般的 Loss Function的形式有：
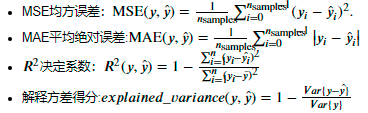求参数值的方法：
（1）最小二乘估计
以估计值与真实值差的平方的和为 Loss Function，对 Loss Function求关于参数的导数，得到 Loss Function取极小值时参数所对应的值。
（2）几何法
（3）极大似然估计
假设噪声的分布已知，通过噪声的分布构造似然函数，通过求似然函数的极值求解参数的值。
- 线性模型的推广
对于分布是非线性的数据，我们可以采取以下几种方法进行建模。
（1）多项式回归
注：多项式的阶数不能过高，若多项式的阶数过高，会产生过拟合的现象，使得模型缺乏泛型。
（2）GAM模型
（3）回归树模型
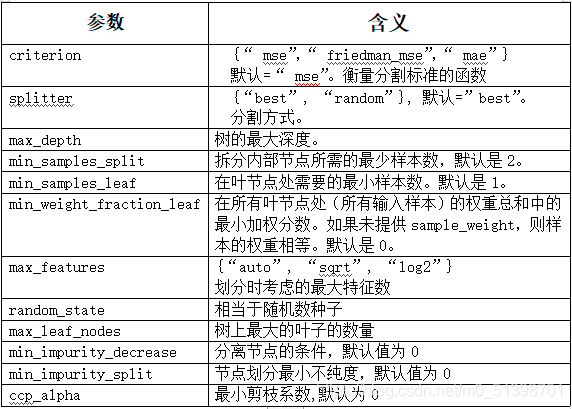
（4）支持向量机回归（SVR)
作业
（2）极大似然估计与最小二乘估计的联系与区别
区别：在极大似然估计中，要假设噪声服从正态分布，只有在已知分布的情况下，才能够构造出似然函数。而在最小二乘估计中不需要做出假设。
联系：极大似然估计与最小二乘估计的结果相同。
（3）为什么多项式回归在实际问题中的表现经常不是太好？
多项式回归模型次数越高，曲线就越光滑，在边界处的置信区间增大，预测效果的稳定性降低
（5）什么是KKT条件？
（6）为什么要引入原问题的对偶问题？
对偶问题是一个凸优化问题，凸优化问题在最优化理论较为简单。
（7）
参考：
[1] https://github.com/datawhalechina/ensemble-learning