误差和梯度下降
1. 误差的来源
如果我们想要更具针对性的优化我们的算法,我们便需要知道我们的误差到底来自于哪里
首先,我们要知道:
e
r
r
o
r
=
b
i
a
s
+
v
a
r
i
a
n
c
e
error = bias + variance
error=bias+variance
1.1 error (误差)
- 反映的是整个模型的准确度
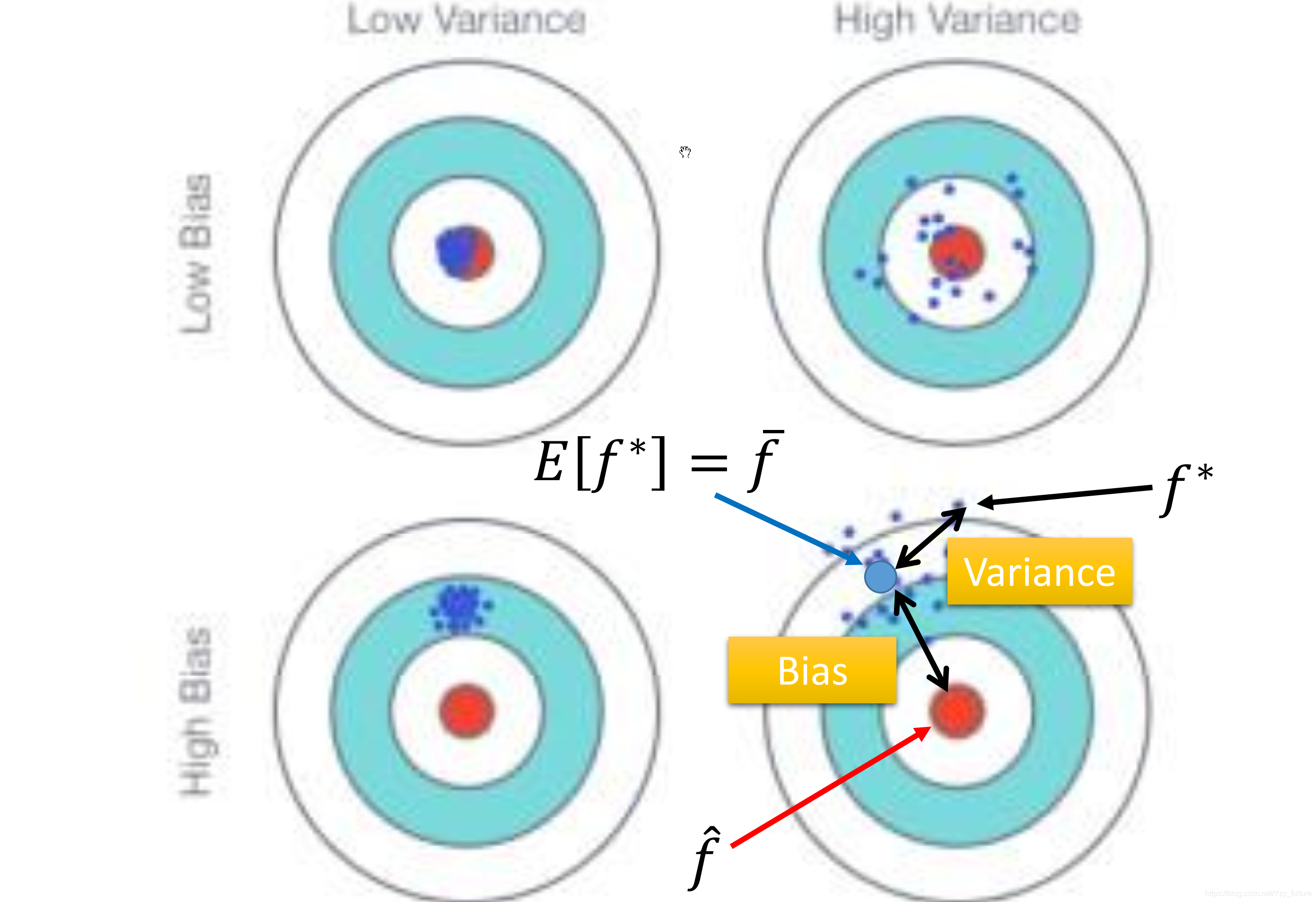
1.2 bias(偏差)
- 反映的是模型在样本上的输出与真实值之间的误差,即模型本身的精准度
1.3 variance (方差)
- 反映的是模型每一次输出结果与模型输出期望之间的误差,即模型的稳定性。
1.4 举例说明
- 目标:打靶打到10环
- 事实:打了7环
- 原因:
- 瞄准出问题,假如瞄准时瞄准的是8环,那么此时 b i a s = 2 bias = 2 bias=2,反映的是模型期望与真实值的差距
- 枪自身稳定性的问题:瞄准的是8环,但打到的是7环,此时 v a r i a n c e = 1 variance = 1 variance=1,反映的是由于模型自身稳定性的问题造成实际结果与模型期望之间的差距
1.5 偏差方差困境
- 基本原理:无法同时降低偏差和方差,只能在两者之间取得平衡。
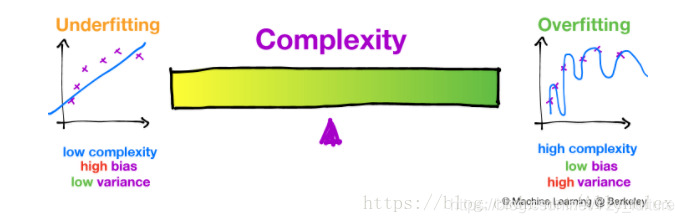
- 解释:如果你想降低偏差,那么你就要增加模型的复杂度,从而能够更好的拟合所给的数据,防止欠拟合的产生。但是,如果此时的模型过于复杂,便会导致过拟合的产生,从而导致模型的泛化性能的下降。所以,需要找到一个两者的平衡点。
- 如下图所示:
2 估测
2.1 估测X的偏差
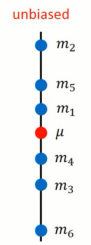
2.1.1 估测平均值
- 拿到N个样本点 x 1 , x 2 , . . . x n {x^1, x ^2, ... x^n} x1,x2,...xn
- 计算N个样本的平均值
m
m
m
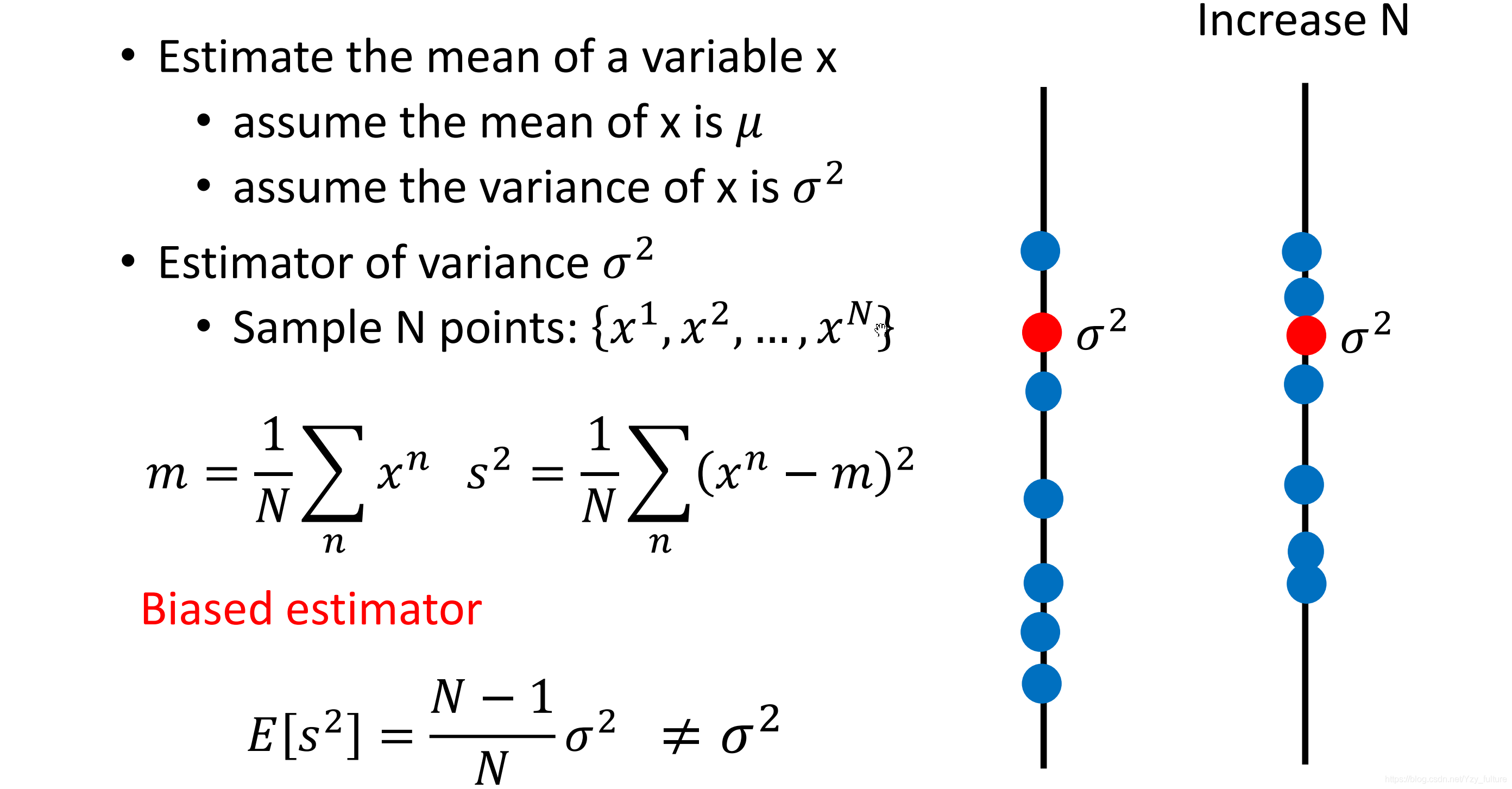
2.1.2 估测方差
2.2 为什么会有多个模型
由于训练集的不同,会导致使用同一个模型所找到的
f
?
f^*
f?不同
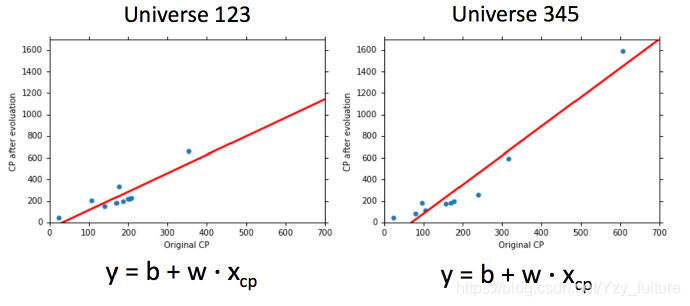
同时,使用不同的模型,使用同一个训练集找到的
f
?
f^*
f?也不同
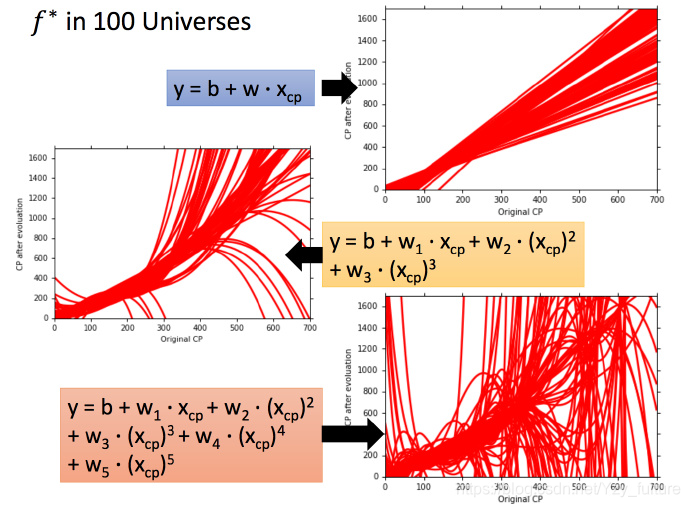
3 判断分析
3.1 欠拟合-偏差大
- 原因:模型的假设空间中并不包含事实
- 解决方法:重新设计模型
- 加入更多的函数
- 考虑更高次的幂、更复杂的模型
- 不建议收集更多数据来解决(事实并不在假设空间中)
3.2 过拟合
- 原因:学习能力过强
- 解决方法:
- 收集更多的数据
- 降低模型的复杂度
4 比较检验
4.1 交叉验证
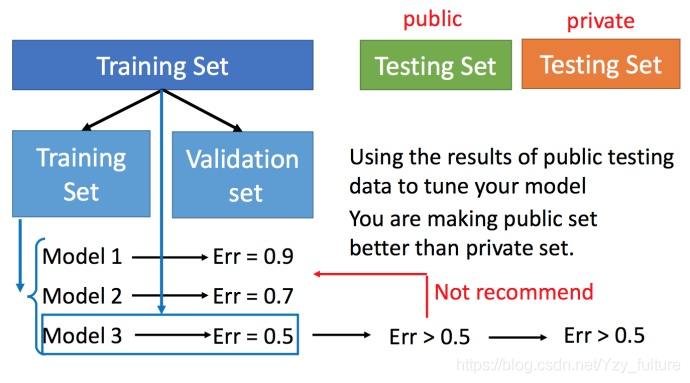
4.2 N折交叉验证
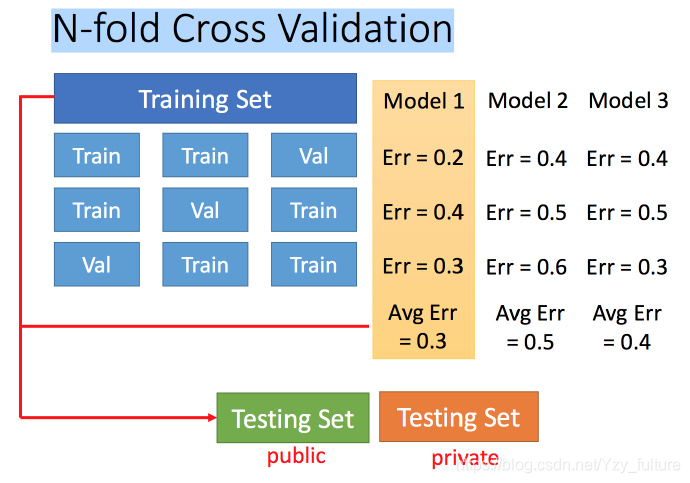
5. 梯度下降
将梯度下降算法进行可视化
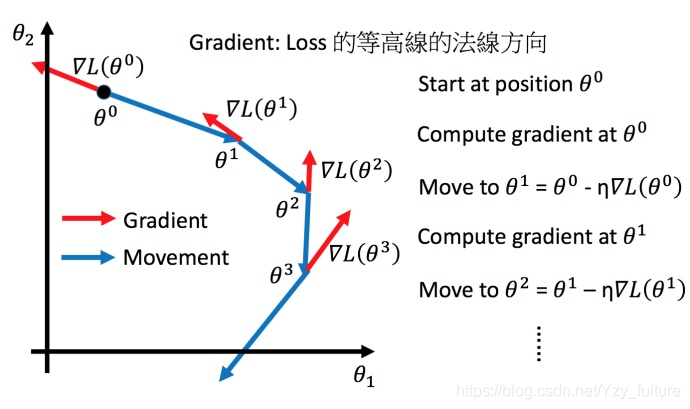
5.1 学习率的调整( η \eta η)
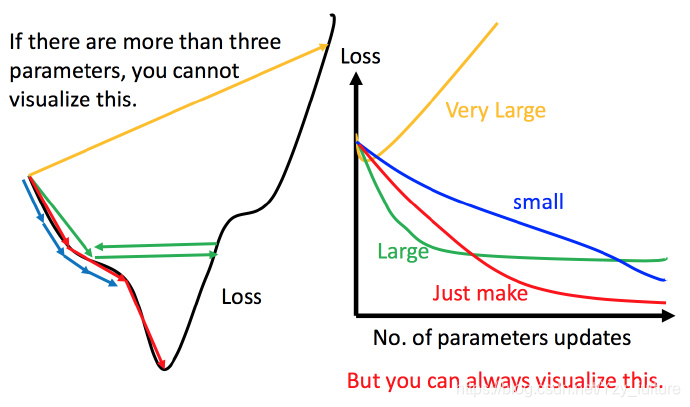
5.1.1 一般学习率的调整
- 学习率调整的刚刚好:红色的线,就能顺利找到最低点。
- 学习率调整的太小:比如蓝色的线,就会走的太慢,虽然这种情况给足够多的时间也可以找到最低点,实际情况可能会等不及出结果。
- 学习率调整的有点大:比如绿色的线,就会在上面震荡,走不下去,永远无法到达最低点。
- 非常大,比如黄色的线,直接就飞出去了,更新参数的时候只会发现损失函数越更新越大。
5.1.2 自适应调整学习率
- 原因:我们想要在开始的时候学习率大一点从而增大步长,随着迭代次数的增加不断地减小步长,从而能够是我们能够更快的收敛到最优解。
- 通常刚开始,初始点会距离最低点比较远,所以使用大一点的学习率
- update好几次参数之后呢,比较靠近最低点了,此时减少学习率
-
Adagrad 算法
- 是什么:每个参数的学习率都把它除上之前微分的均方根
- 解释:
- 普通的梯度下降为:
w t + 1 = w t ? η t g t w^{t+1} = w^t - \eta^tg^t wt+1=wt?ηtgt
η t = η t t + 1 \eta^t = \frac{\eta^t }{\sqrt{t+1}} ηt=t+1?ηt? - 而adagrad算法可以做的更好
w t + 1 = w t ? η t σ t g t w^{t+1} = w^t - \frac{\eta^t }{\sigma^t}g^t wt+1=wt?σtηt?gt
g t = ? L ( θ t ) ? w g^t = \frac{\partial{L(\theta^t)}}{\partial w} gt=?w?L(θt)?
- 普通的梯度下降为:
- 矛盾:
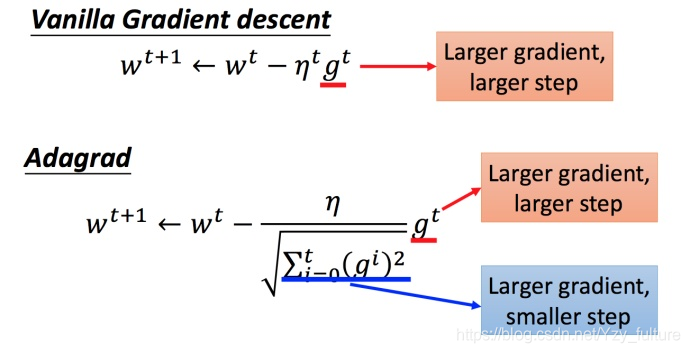
梯度越大的时候,步伐应该越大,但下面分母又导致当梯度越大的时候,步伐会越小
解释:
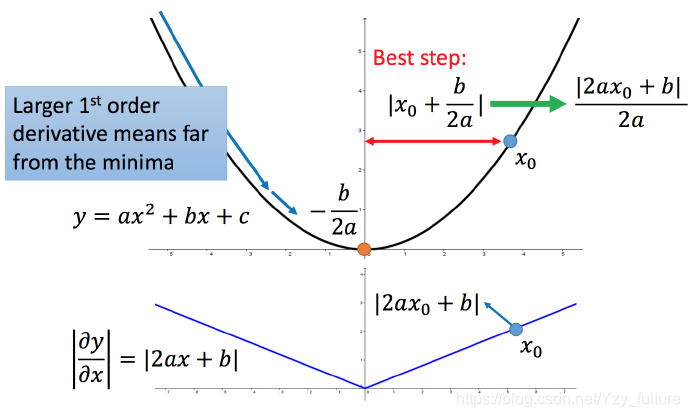
比如初始点在 x 0 x_0 x0?,最低点为 ? b 2 a ?\frac{b}{2a} ?2ab?,最佳的步伐就是 x0x0 到最低点之间的距离 ∣ x 0 + b 2 a ∣ |x_0 + \frac{b}{2a}| ∣x0?+2ab?∣。而 ∣ 2 a x 0 + b ∣ |2ax_0 +b| ∣2ax0?+b∣就是方程绝对值在 x 0 x_0 x0?这一点的微分。
这样可以认为如果算出来的微分越大,则距离最低点越远。而且最好的步伐和微分的大小成正比。所以如果踏出去的步伐和微分成正比,它可能是比较好的。
从而得出结论:梯度越大,就跟最低点的距离越远。
但结论在多个参数的时候就不一定成立
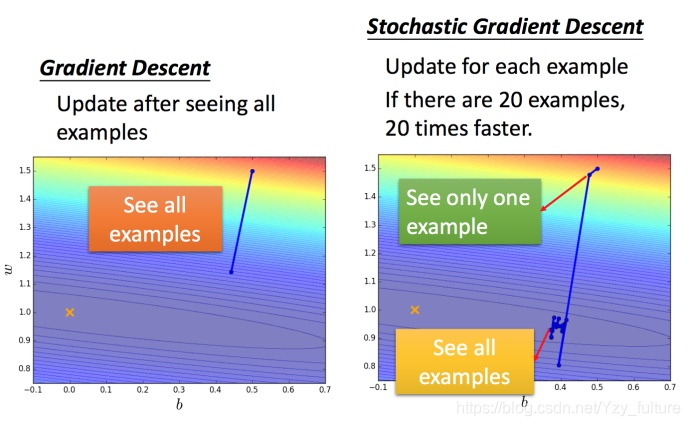
5.2 随机梯度下降法
特点:损失函数不需要处理训练集所有的数据,选取一个例子
x
n
x^n
xn即可。
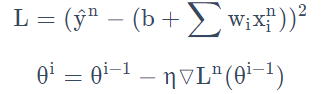
不需要像之前那样对所有的数据进行处理,只需要计算某一个例子的损失函数
L
n
L_n
Ln?,就可以赶紧更新梯度
5.3 特征缩放
将具有不同输入范围的输入范围进行缩放,使得不同输入的范围一样
5.3.1 缩放的原因
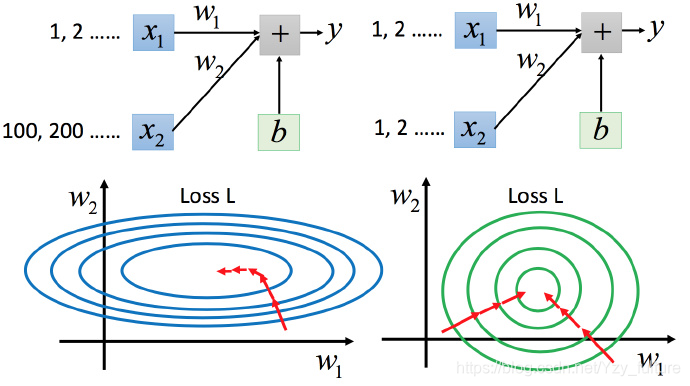
- 为了使不同的特征值对输出的影响相近
- 为了使梯度下降时参数的更新更加容易、有效。
5.3.2 特征缩放的方法
下面为较为常见的一种
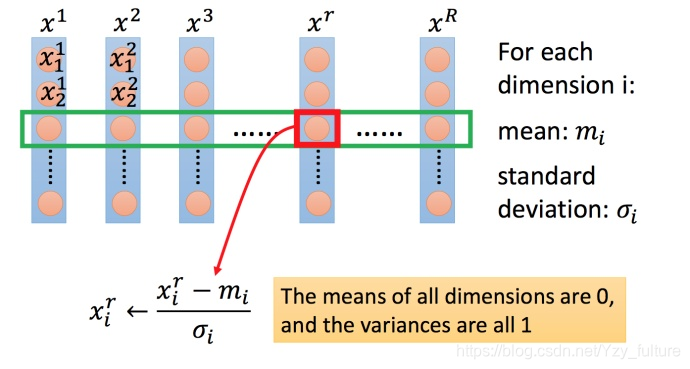
- 对每一个维度 i i i(绿色框)都计算平均数,记做 m i m_i mi?;计算标准差,记做 σ i \sigma_i σi?.
- 然后用第 r r r个例子中的第 i i i个输入,减掉平均数 m i m_i mi? ,然后除以标准差 σ i \sigma_i σi?,得到的结果是所有的维数都是 0,所有的方差都是1
总结
这两节就开始涉及到了较多的公式推导,自己由于数学基础的问题感觉遇到了一些问题。所以此次写的不是很详细。之后会不断地完善。
谢谢~