1、误差从哪里来
- Bias
- Variance
从实际的训练数据中寻找出f*
F hat则是最佳的function,能实际准确得到y的function
f*是对f hat的一个估计,两者还是有差距
模型简单的时候bias大,variance小,function space可能都没有包含目标function
而模型复杂的时候variance大,bias小,function space也较大,更可能包含目标function
随着模型的bias造成的error逐渐下降
variance造成的误差变得越来越大(像打把时? 瞄的准,瞄在了中心? 但可能误差越来越大)
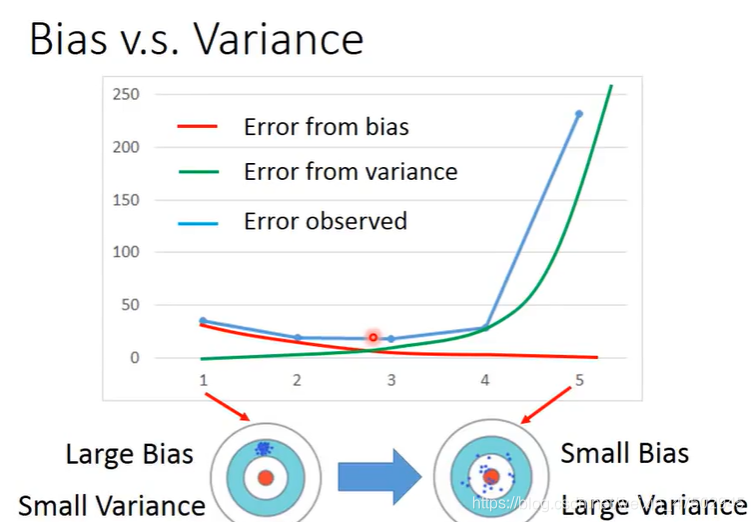
两种误差合起来就是蓝色的线,存在一个均衡点使两者误差和最小
误差来自bias很大——underfitting
误差来自variance很大——overfitting
弄明白这个有助于搞清改进的方向
如何诊断:
1、如果样本甚至无法拟合样本中少数几个点,说明模型与正确的模型有较大的差距,即bias大,underfitting
2、如果在训练集上能够较好地拟合,但在测试集上有较大的误差,这说明可能有较大的variance,存在过拟合的情况
针对这两种问题不同的解决方法:
1、underfitting:重新设计模型使之变得更复杂有更好的解释能力,使function set 尽可能去包含正确的function
2、overfitting:
1)增加数据:不会伤害bias,但可能收集数据比较困难;或者在某些情况下自己增加更多数据,图片翻转等
2)正则化:能够是function更平滑
N-fold cross validation
(K 折交叉验证)
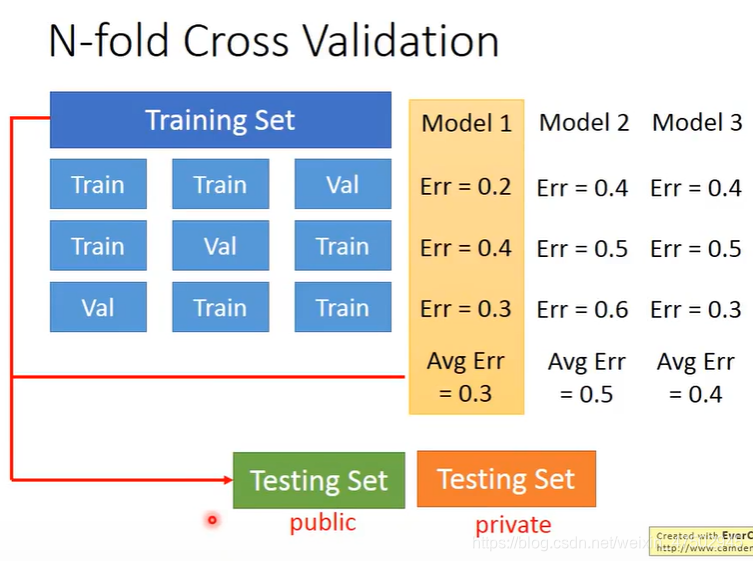
把训练集分成几份,依次把其中的某一份作为验证集,另外几份作为训练集
分别算不同模型,在不同的部分做验证集时平均误差,进行比较
选出效果最好的模型,在完整的训练集上做训练,再在测试集上去做测试
梯度下降

Learning rate的调整
太小,调整地太慢
太大,调整地太快,直接跳过了最小值
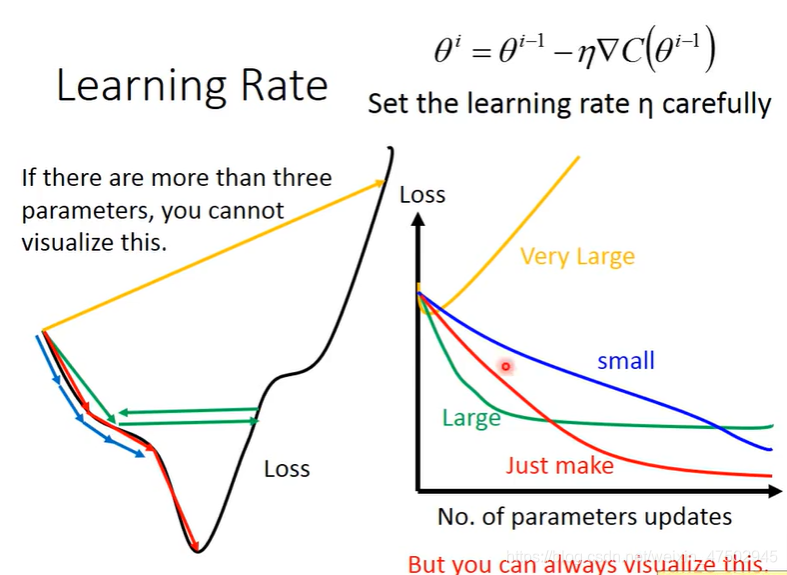
可以将参数变化与loss 变化画在坐标轴上
Learning rate太小,蓝色线:下降缓慢
Learning rate较大,绿色线:loss下降快,但很快会卡住不再下降
Learning rate太大,黄色线:loss激增,多走一步甚至超过了最低点
自动调整learning rate
1、基本想法:通常learning rate会随着参数的更新而逐渐变小,起始点时离loss最低点较远,一开始调整幅度可以大一点,,当越来越接近时,learning rate变小
2、最好的情况是给每个不同的参数都单独设置不同的learning rate
adagrad:
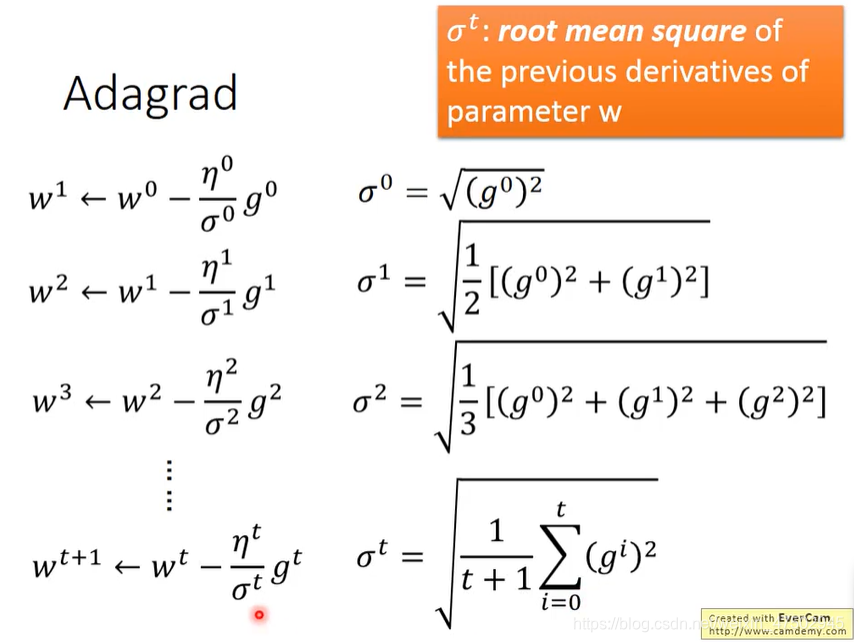

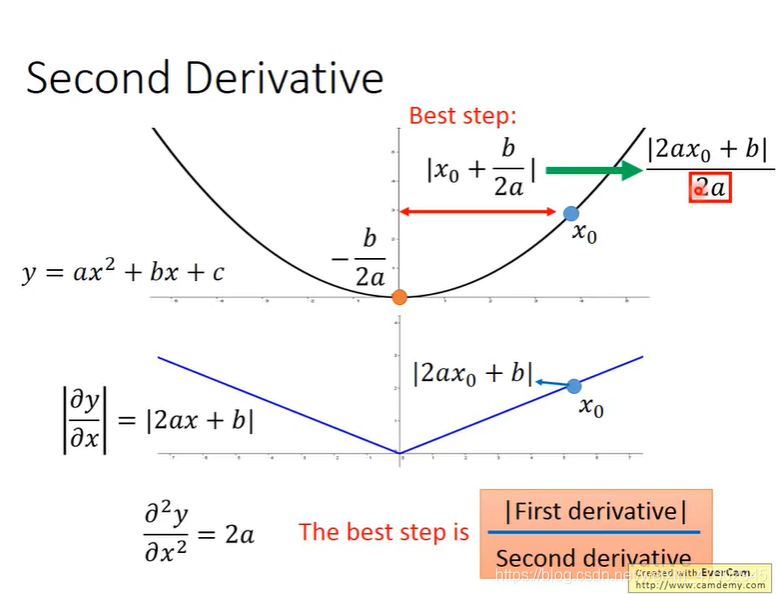
最好的step(步长):分子与一次微分成正比,与二次微分成反比
当有多个参数的时候
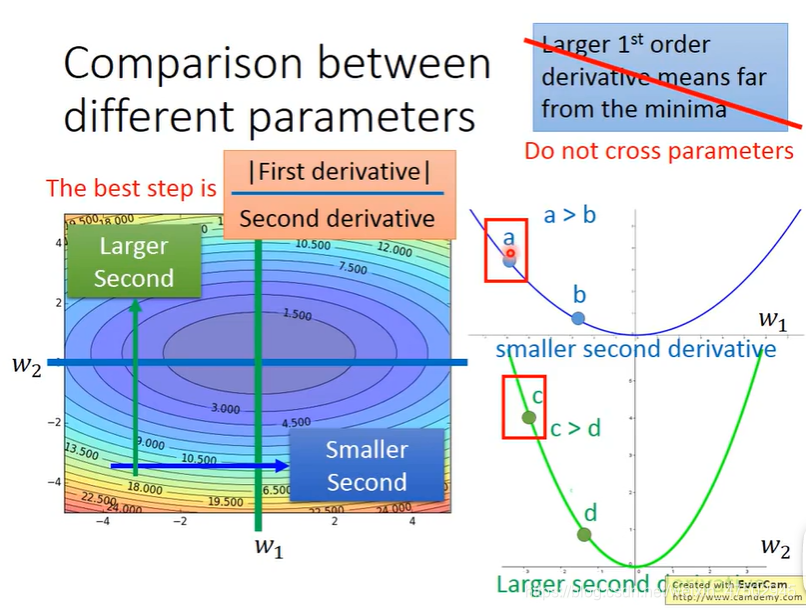
要想比较a和c点到最低点的距离,光是比较一次微分还不够,
a点对w1的微分值更小
c对对w2的微分值更大??
根据微分值更大离最低点更远这个原则来看,c点微分值比在a点的大,按理应该离最低点更远,实际却离最低点比a点更近,与原则相矛盾,原因是右上角蓝色的原则不能跨参数使用。
当需要同时考虑好几个参数:
需要引入二次微分来描述不同参数对应的函数的陡峭平滑程度,
W1对应函数的二次微分比较小,
W2对应函数的二次微分比较大,
要把二次微分(该点一次微分值/二次微分值)考虑进去
才能将a点和c点现在位置到最低点的距离进行比较
Stochastic gradient descent
随机梯度下降
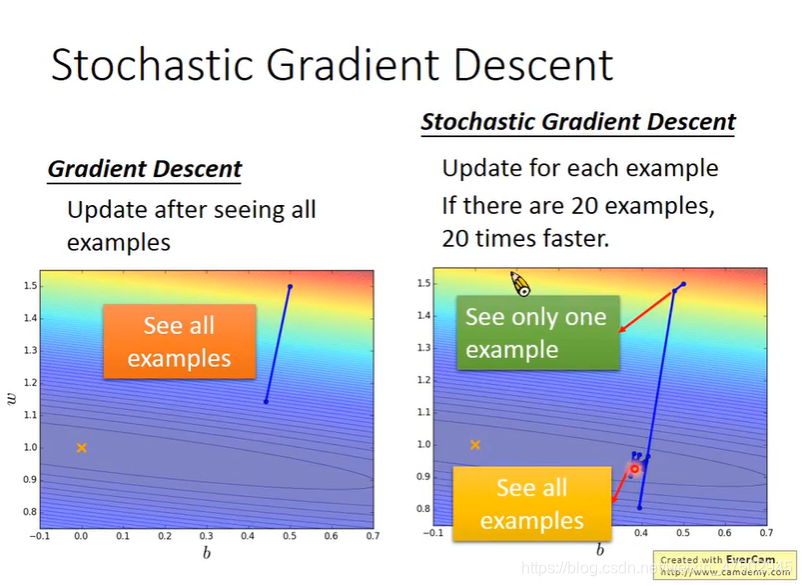
gradient descent:计算所有的data,然后更新参数
Stochastic gradient descent:只计算某一个样本的loss,然后就更新参数
SGD优点:算的快,对噪声不敏感
Feature scaling
特征缩放
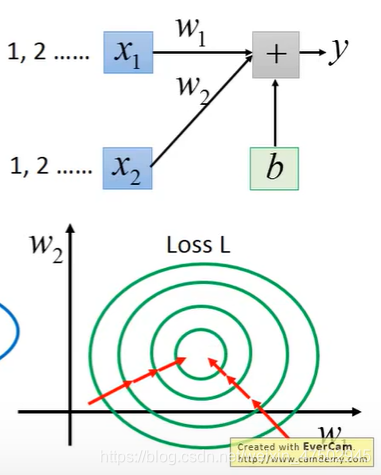
当输入值有两个x1,x2时,若x1,x2的分布差别较大时,做缩放使不同的特征变量的特征是相似的
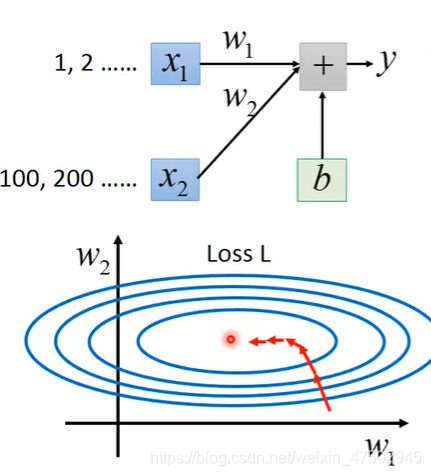
因为如果两个变量的范围不同,一个特征x1的取值是1,2,3……,另一个特征x2的取值为100,200,300……,
因此w1有较小的微分,对loss影响较小;
W2有较大的微分,对loss的影响较大。这种情况更新参数比较困难,需要做adagrad,不同方向上要有不同的learning rate,并且顺着等高线法线方向走,并不会指向中心
若x1,x2的scale比较接近,画出来的图是接近圆形的,更新参数较容易,
并且区域中的任何点都是指向最低点
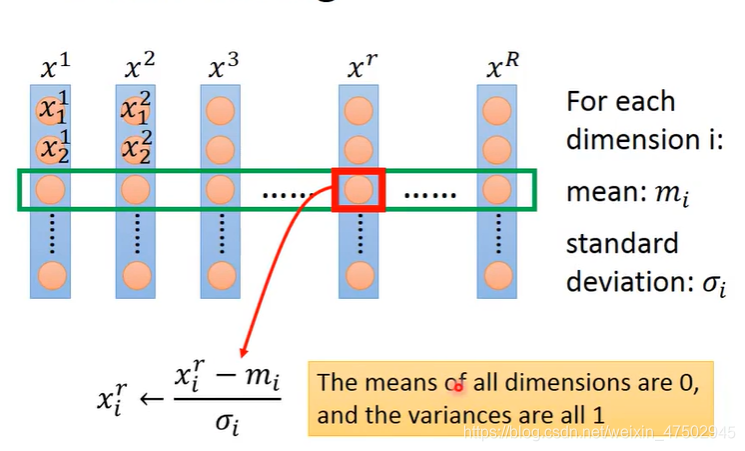
如何做scaling
对每一个维度 i都计算它的平均值mi,标准差σi
对第r组数据的第i个component(即第i个特征)减去平均值mi后再除以标准差σi
为什么梯度下降会有效
每次更新完参数,loss不一定会下降,有可能还会上升
泰勒公式:

当x0接近x的时候,(x-x0)^2及之后的项远小于x-x0这一项,因此就可以把二次以后的都略去

当有多个参数时,方法相似,对h(x,y)分别在x0和y0处做偏微分
要求L(θ)的最小值,当θ1,θ2在给定的圆圈范围内时(圆圈的圆心坐标为(a,b)),根据向量的知识可知,(δθ1,δθ2)的方向与(u,v)的方向相反时即可有最小的L(θ),用式子表示如下,负号表示(δθ1,δθ2)的方向与(u,v)的方向相反;η与圆的半径成正比,因为要使η乘上[u,v]的长度刚好等于圆的半径
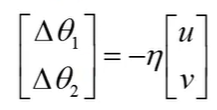
再将δθ1,δθ2变成θ1,θ2,只需要分别加上a,b即可
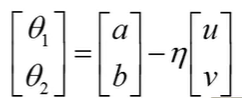

该式子成立的条件是圆的半径要足够小,使泰勒公式够精确
即η(与红色圆圈的半径成正比)要足够小,即learning rate要足够小,否则泰勒公式不成立(泰勒公式要求θ1足够接近a,θ2足够接近b)
如果考虑到泰勒公式中的二次式也可以,但会更复杂
梯度下降的限制
1、可能会卡在局部最小的地方
2、鞍点(saddle point)的地方微分值也可能是0
3、可能卡在高原,误以为微分值很小的时候就是接近局部最小值了
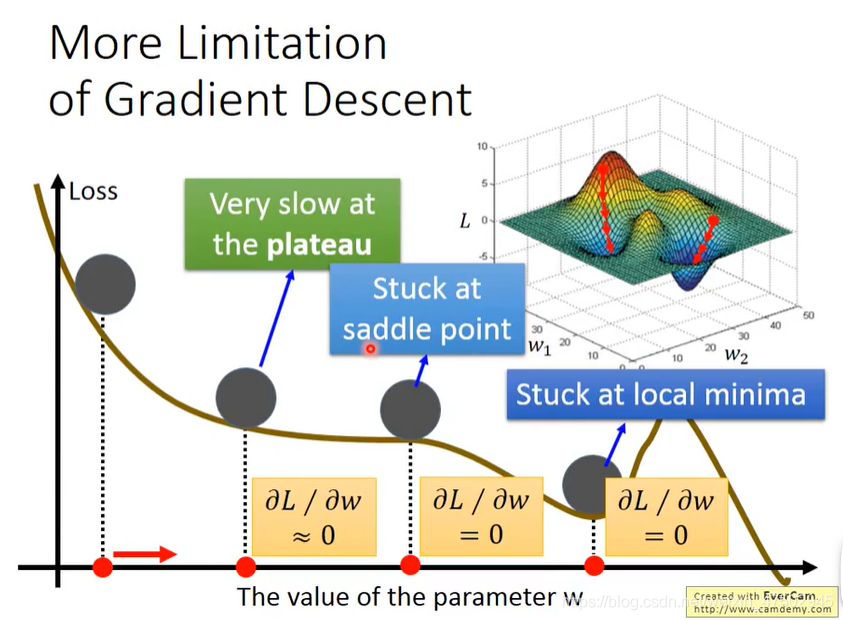
*图源自李宏毅《机器学习》视频