人工智能的浪潮正在席卷全球,诸多词汇时刻萦绕在我们耳边:人工智能(Artificial Intelligence)、机器学习(Machine Learning)、深度学习(Deep Learning)。本文主要是对李宏毅课程内容进行笔记梳理,参考链接在文末已经给出。
5-误差从哪来?
Error的来源
定义与理解
Error = Bias(偏差) + Variance(方差)
- Error反映的是整个模型的准确度。
- Bias反映的是模型在样本上的输出与真实值之间的误差,即模型本身的精准度。
- Variance反映的是模型每一次输出结果与模型输出期望之间的误差,即模型的稳定性。
以打靶子为例: - error反映的是打的准不准,成绩好不好。
- Bias反映的是瞄的准不准,眼神好不好使。
- Variance反映的是枪稳不稳,手拿枪拿的稳不稳。
举一个例子,一次打靶实验,目标是为了打到10环,但是实际上只打到了7环,那么这里面的Error就是3。具体分析打到7环的原因,可能有两方面:
- 是瞄准出了问题,比如实际上射击瞄准的是9环而不是10环;
- 是枪本身的稳定性有问题,虽然瞄准的是9环,但是只打到了7环。
那么在上面一次射击实验中,Bias就是1,反应的是模型期望与真实目标的差距,而在这次试验中,由于Variance所带来的误差就是2,即虽然瞄准的是9环,但由于本身模型缺乏稳定性,造成了实际结果与模型期望之间的差距。
还有其他的解释方式,例如经典的靶子图
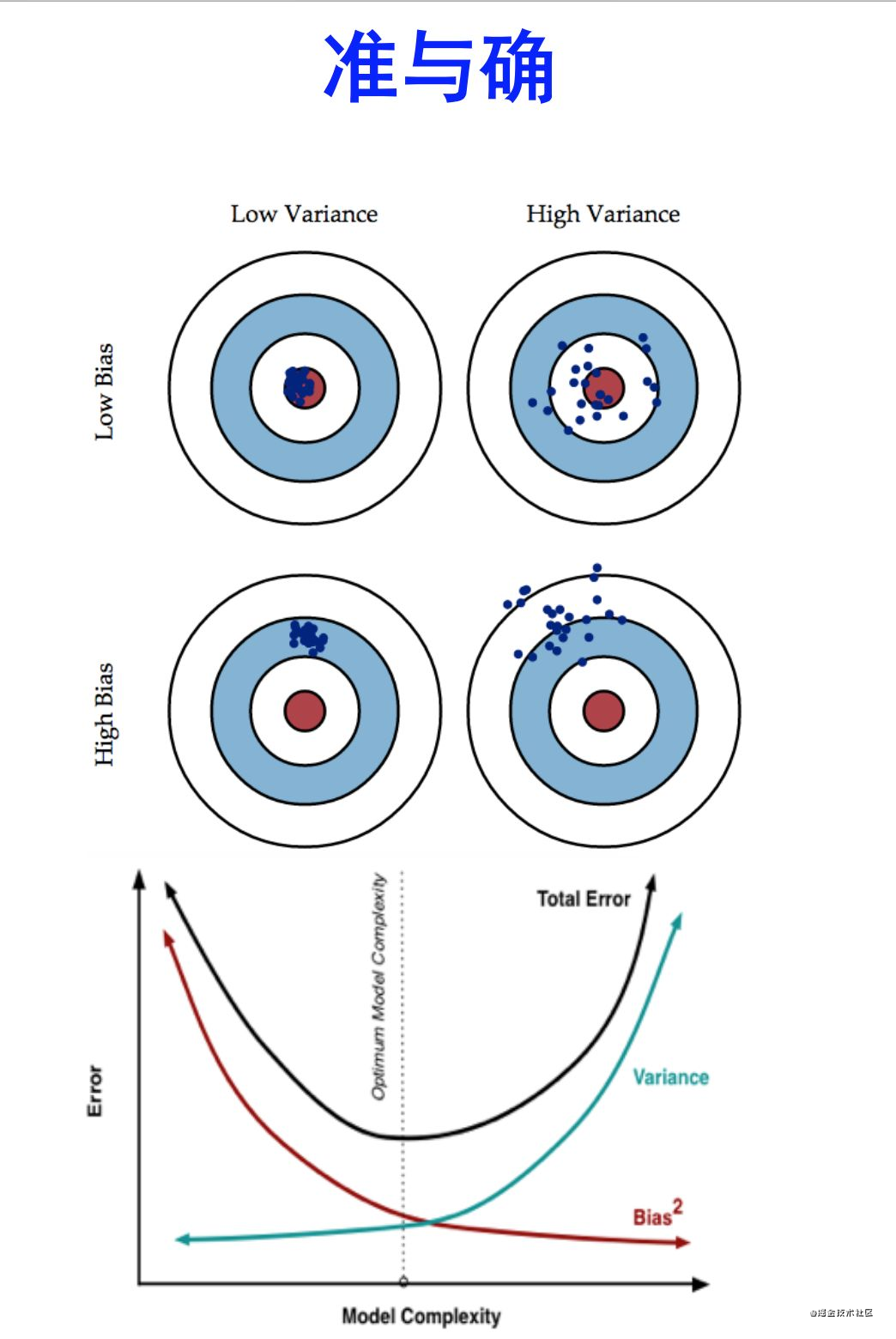
把Bais和Variance抽象为准与确的关系:
- 准: 简单讲,就是在样本上拟合的好不好。要想在bias上表现好low bias,就得复杂化模型,增加模型的参数,但这样容易过拟合(overfitting),过拟合对应上图是[low bais,high variance],点很分散。low bias对应就是点都打在靶心附近,所以瞄的是准的,但手不一定稳。
- 确: varience描述的是样本上训练出来的模型在测试集上的表现,要想在variance上表现好,low varience,就要简化模型,减少模型的参数,但这样容易欠拟合(ufiting),欠拟合对应上图是[low variance,high bias],点偏离中心。low variance对应就是点都打的很集中,但不一定是靶心附近,手很稳,但是瞄的不准。
方差与偏差与欠、过拟合的关系
一般来说,简单的模型会有一个较大的偏差和较小的方差,复杂的模型偏差较小方差较大。这也引申出欠拟合和过拟合的概念。
- 欠拟合:模型不能适配训练样本,有一个很大的偏差(模型不适配训练样本太简单——偏差大——欠拟合)
- 过拟合:模型很好适配训练样本,但在测试集上表现很糟,有一个很大的方差(模型过度适配训练样本太复杂——方差大——过拟合。
在一个实际系统中,Bias与Variance往往是不能兼得的。如果要降低模型的Bias,就一定程度上会提高模型的Variance,反之亦然,如下图所示:
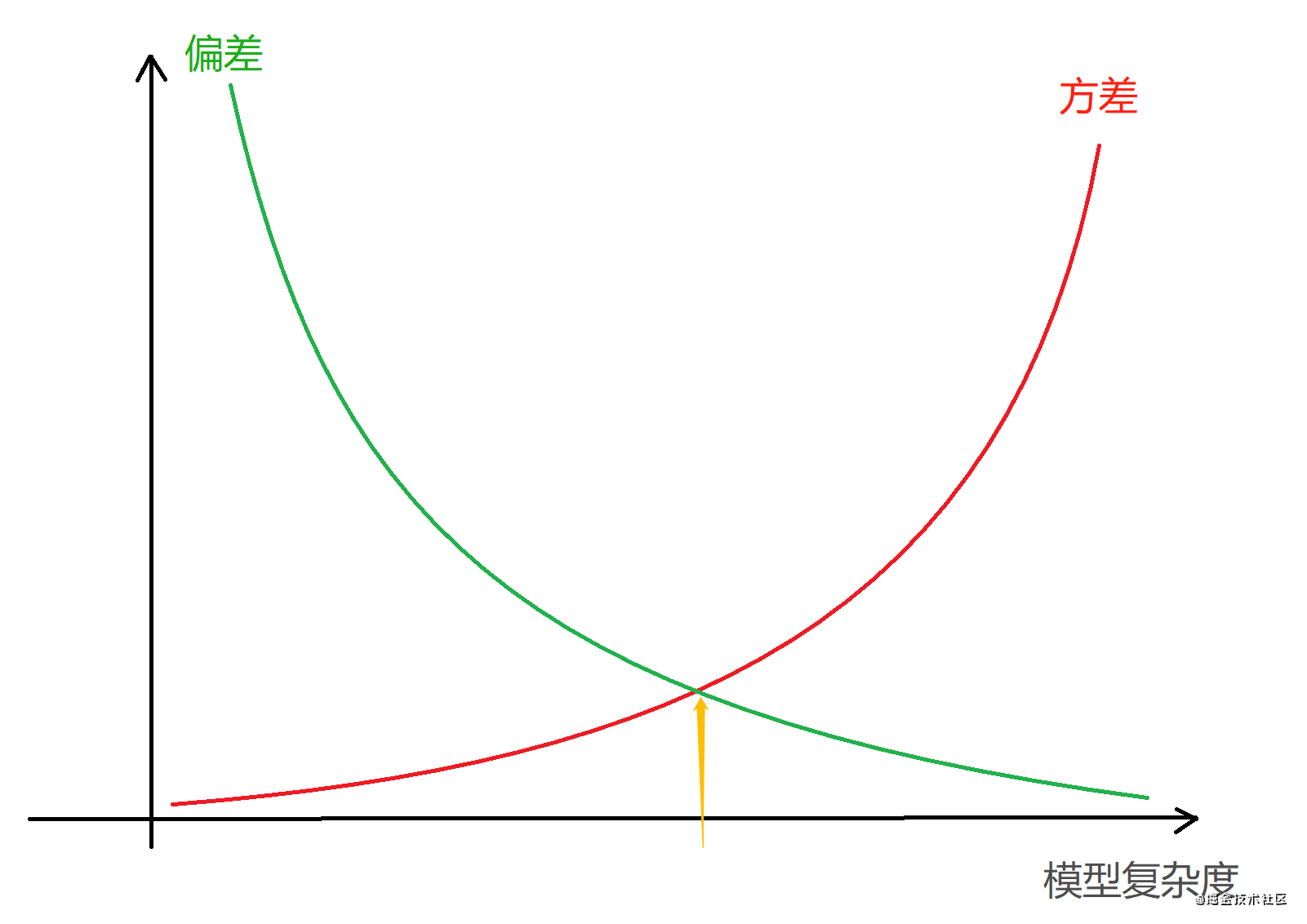
如何处理方差与偏差问题?
整体思路: 首先,要知道方差和偏差是无法完全避免的,只能尽量减少其影响。
- 在避免偏差时,需尽量选择正确的模型,一个非线性问题而我们一直用线性模型去解决,那无论如何,高偏差是无法避免的。
- 有了正确了模型,我们还要慎重选择数据集的大小,通常数据集越大越好,但大到数据集已经对整体所有数据有了一定的代表性后,再多的数据已经不能提升模型了,反而会带来计算量的增加。而训练数据太小一定是不好的,这会带来过拟合,模型复杂度太高,方差很大,不同数据集训练出来的模型变化非常大。
- 最后,要选择模型的复杂度,复杂度高的模型通常对训练数据有很好的拟合能力。
针对偏差和方差的思路:
偏差:实际上也可以称为避免欠拟合
- 寻找更好的特征 – 具有代表性。
- 用更多的特征 – 增大输入向量的维度。(增加模型复杂度)
方差:实际上也可以称为避免过拟合 - 增大数据集合 – 使用更多的数据,噪声点比减少(减少数据扰动所造成的影响(紧扣定义))
- 减少数据特征 – 减少数据维度,高维空间密度小(减少模型复杂度)
- 正则化方法
- 交叉验证法
可以参考查看 机器学习中的Bias(偏差),Error(误差),和Variance(方差)有什么区别和联系?
偏差 - 方差权衡
- 多项式回归
多项式回归模型,我们可以选择不同的多项式的次数,对模型的影响如下。
多项式次数 | 模型复杂度 | 方差 | 偏差 | 过/欠拟合 |
| :—: | :—: | :-: | :-: | :—: |
| 低 | 低 | 低 | 高 | 欠拟合 |
| 中 | 中 | 中 | 中 | 适度 |
| 高 | 高 | 高 | 低 | 过拟合
| 多项式次数 | 模型复杂度 | 训练误差 | 测试误差 |
|---|---|---|---|
| 低 | 低 | 高 | 高 |
| 中 | 中 | 中 | 低 |
| 高 | 高 | 低 | 高 |
- 正则化项
添加正则化项(Regularization)相当于对模型参数施加惩罚,压缩了参数的范围,限制了模型的复杂度,从而有助于缓解模型过拟合问题,选择不同的 正则化项权重λ 对模型的影响如下。
| 正则化项权重λ | 模型复杂度 | 方差 | 偏差 | 过/欠拟合 |
|---|---|---|---|---|
| 大 | 低 | 低 | 高 | 欠拟合 |
| 中 | 中 | 中 | 中 | 适度 |
| 小 | 高 | 高 | 低 | 过拟合 |
| 正则化项权重λ | 模型复杂度 | 训练误差 | 测试误差 |
|---|---|---|---|
| 大 | 低 | 高 | 高 |
| 中 | 中 | 中 | 低 |
| 小 | 高 | 低 | 高 |
- 神经网络
| 神经网络结构 | 模型复杂度 | 方差 | 偏差 | 过/欠拟合 |
|---|---|---|---|---|
| 小 | 低 | 低 | 高 | 欠拟合 |
| 中 | 中 | 中 | 中 | 适度 |
| 大 | 高 | 高 | 低 | 过拟合 |
在《西瓜书》中也会有这种描述:泛化误差=偏差+方差+噪声
其误差的期望值可以分解为三个部分:样本噪音、模型预测值的方差、预测值相对真实值的偏差
公式为:
E
(
(
y
?
f
^
(
x
)
)
2
)
=
σ
2
+
V
a
r
[
f
^
(
x
)
]
+
(
B
i
a
s
[
f
^
(
x
)
]
)
2
E((y?\widehat{f}(x))^2)=σ^2+Var[\widehat{f}(x)]+(Bias[\widehat{f}(x)])^2
E((y?f
?(x))2)=σ2+Var[f
?(x)]+(Bias[f
?(x)])2
其中
B
i
a
s
[
f
^
(
x
)
]
=
E
[
f
^
(
x
)
?
f
(
x
)
]
Bias[\hat{f}(x)] = E[\hat{f}(x) - f(x)]
Bias[f^?(x)]=E[f^?(x)?f(x)]
即:误差的期望值 = 噪音的方差 + 模型预测值的方差 + 预测值相对真实值的偏差的平方
先看一个图比较直观。
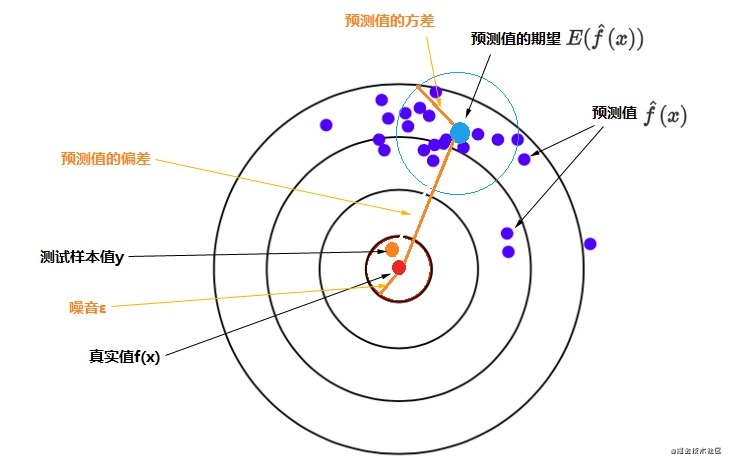
靶心(红点)是测试样本的真实值,测试样本的y(橙色点)是真实值加上噪音,特定模型重复多次训练会得到多个具体的模型,每一个具体模型对测试样本进行一次预测,就在靶上打出一个预测值(图上蓝色的点)。所有预测值的平均就是预测值的期望(较大的浅蓝色点),浅蓝色的圆圈表示预测值的离散程度,即预测值的方差。
模型选择
现在在偏差和方差之间就需要一个权衡 想选择的模型,可以平衡偏差和方差产生的错误,使得总错误最小,对于模型的选择有以下的方法,比如我们拥有三个模型,我们要验证哪种模型表现最好。
交叉验证
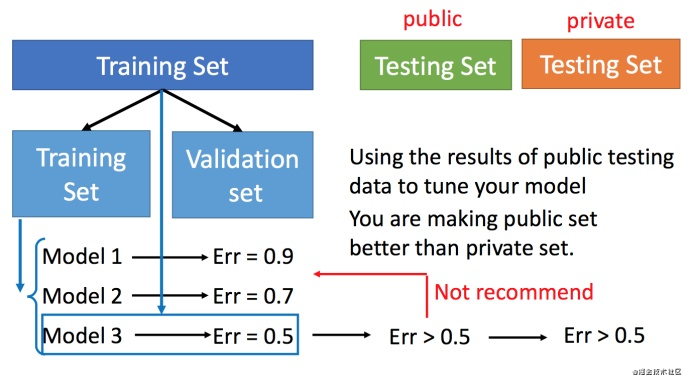
图中public的测试集是已有的,private是没有的,不知道的。交叉验证 就是将训练集再分为两部分,一部分作为训练集,一部分作为验证集。用训练集训练模型,然后再验证集上比较,确实出最好的模型之后(比如模型3),再用全部的训练集训练模型3,然后再用public的测试集进行测试,此时一般得到的错误都是大一些的。不过此时会比较想再回去调一下参数,调整模型,让在public的测试集上更好,但不太推荐这样。
上述方法可能会担心将训练集拆分的时候分的效果比较差怎么办,可以用下面的方法。
N-折交叉验证
将训练集分成N份,比如分成3份,然后在其中将每一份分别作为验证集去训练N次三种模型,然后将每个模型N次的平均error作为最终的评判标准。
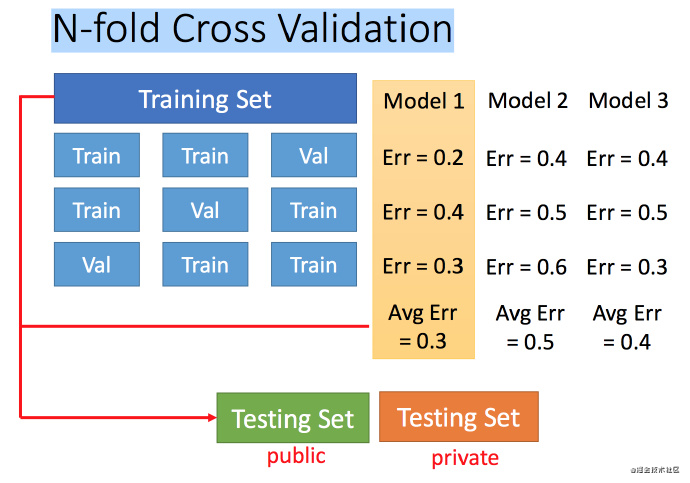
比如在三份中训练结果Average错误是模型1最好,再用全部训练集训练模型1。
6-梯度下降
在回归问题的第三步中,需要解决下面的最优化问题:
θ
?
=
a
r
g
θ
m
i
n
L
(
θ
)
θ^?=arg_θminL(θ)
θ?=argθ?minL(θ)
- L?:lossfunction(损失函数)
- θ?:parameters(参数)
这里的parameters是复数,即 θ?指代一堆参数。
我们要找一组参数θ?,让损失函数越小越好,这个问题可以用梯度下降法解决。分别计算初始点处,两个参数对?L?的偏微分,然后? θ 0 \theta^0 θ0?减掉? η \eta η?乘上偏微分的值,得到一组新的参数。(η?叫做Learning rates(学习速率))。
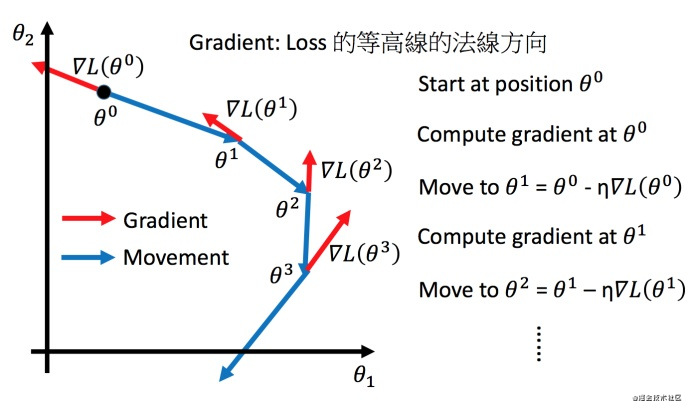
调整学习速率
小心地调整学习速率
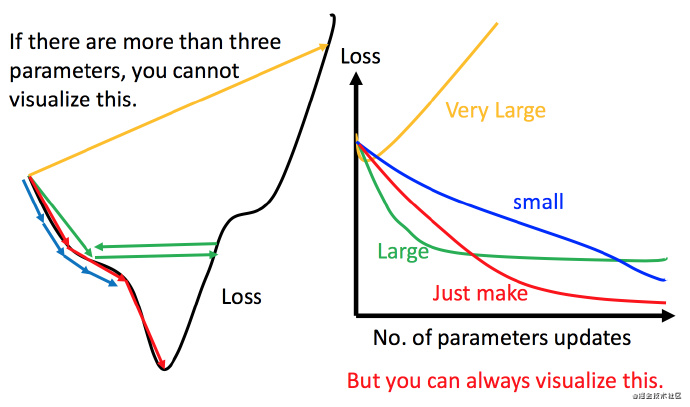
解决方法就是上图右边的方案,将参数改变对损失函数的影响进行可视化。比如学习率太小(蓝色的线),损失函数下降的非常慢;学习率太大(绿色的线),损失函数下降很快,但马上就卡住不下降了;学习率特别大(黄色的线),损失函数就飞出去了;红色的就是差不多刚好,可以得到一个好的结果。
虽然这样的可视化可以很直观观察,但可视化也只是能在参数是一维或者二维的时候进行,更高维的情况已经无法可视化了。
自适应学习率
举一个简单的思想:随着次数的增加,通过一些因子来减少学习率
- 通常刚开始,初始点会距离最低点比较远,所以使用大一点的学习率
- update好几次参数之后呢,比较靠近最低点了,此时减少学习率
- 比如? η t = η t t + 1 \eta^t =\frac{\eta^t}{\sqrt{t+1}} ηt=t+1?ηt?,t?是次数。随着次数的增加, η t \eta^t ηt?减小
学习率不能是一个值通用所有特征,不同的参数需要不同的学习率
Adagrad算法
定义及公式形式
定义: 每个参数的学习率都把它除上之前微分的均方根。
普通的梯度下降为:
w t + 1 ← w t ? η t g t w^{t+1}←w^t?η^tg^t wt+1←wt?ηtgt
η t = η t t + 1 \eta^t=\frac{\eta^t}{\sqrt {t+1}} ηt=t+1?ηt?
w?是一个参数
Adagrad公式为:
w t + 1 ← w t ? η t σ t g t w^{t+1}←w^t-\frac{\eta^t}{\sigma^t}g^t wt+1←wt?σtηt?gt
g t = ? L ( θ t ) ? w g^t=\frac{?L(\theta^t)}{?w} gt=?w?L(θt)?
Adagrad更新过程:
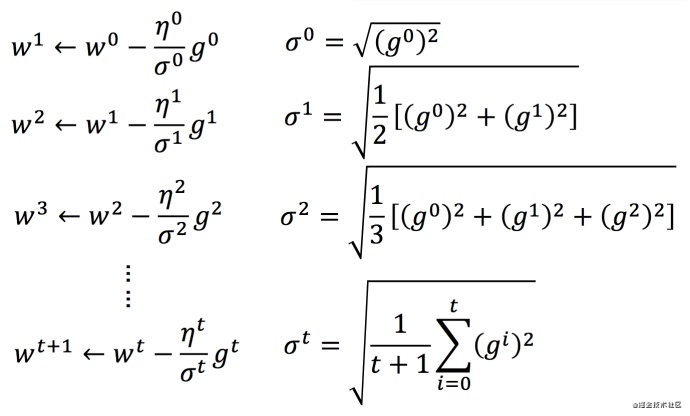
将 Adagrad 的式子进行化简:
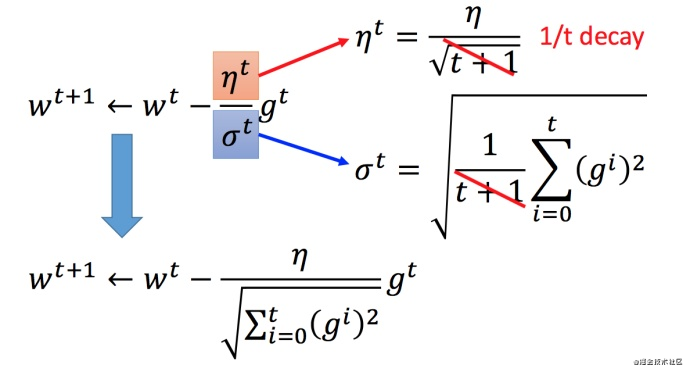
最终Adagrad形式:
w t + 1 ← w t ? η ∑ i = 0 t ( g i ) 2 g t w^{t+1}←w^t-\frac{\eta}{\sqrt {\displaystyle \sum^{t}_{i = 0}{(g^i)^2}}}g^t wt+1←wt?i=0∑t?(gi)2?η?gt
Adagrad的矛盾
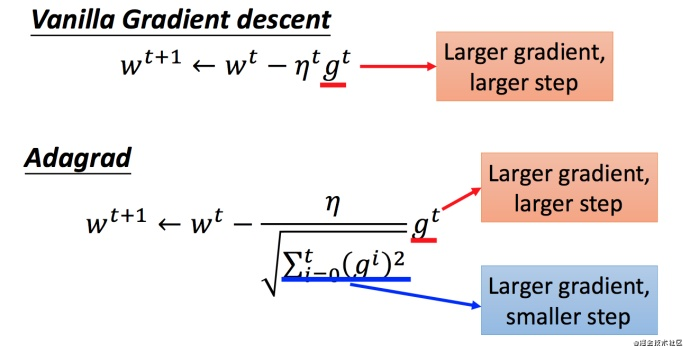
很多人会问,在 Adagrad 中,当梯度越大的时候,步伐应该越大,但下面分母又导致当梯度越大的时候,步伐会越小。这不就是和梯度下降的思想矛盾了吗?(同时随着梯度的增大,我们的分母是在逐渐增大,也就对整体学习率是减少的,这是为什么呢?)
答:这是因为随着我们更新次数的增大,我们是希望我们的学习率越来越慢。因为我们认为在学习率的最初阶段,我们是距离损失函数最优解很远的,随着更新的次数的增多,我们认为越来越接近最优解,于是学习速率也随之变慢。
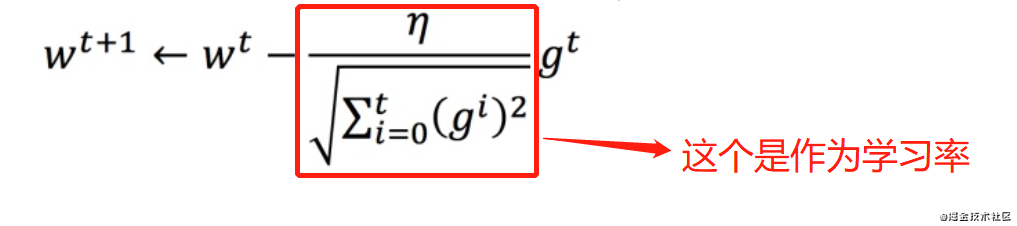
图中红色方框作为整体的学习率,随着迭代次数的增加,最正常的情况就是我们逐渐接近最优解,就算梯度很大,也应该降低学习率去逐步逼近最优解
随机梯度下降法
随机梯度下降法更快,损失函数不需要处理训练集所有的数据,选取一个例子? x n x^n xn
L = ( y n ? ( b + ∑ w i x i n ) ) 2 L=(y^n?(b+∑w_i{x_i}^n))^2 L=(yn?(b+∑wi?xi?n))2
$θ^i
=θ^{
i?1}
?η▽L(θ{
i?1})
$
此时不需要像之前那样对所有的数据进行处理,只需要计算某一个例子的损失函数Ln,就可以赶紧update 梯度。例如:
常规梯度下降法走一步要处理到所有二十个例子,但随机算法此时已经走了二十步(每处理一个例子就更新)
特征放缩
比如有个函数:
y = b + w 1 ? x 1 ? + w 2 ? x 2 y=b+w_ 1?x_ 1?+w_ 2?x_ 2 y=b+w1??x1??+w2??x2?
两个输入的分布的范围很不一样(两个特征的数量范围差距很大)建议把他们的范围缩放,使得不同输入的范围是一样的。
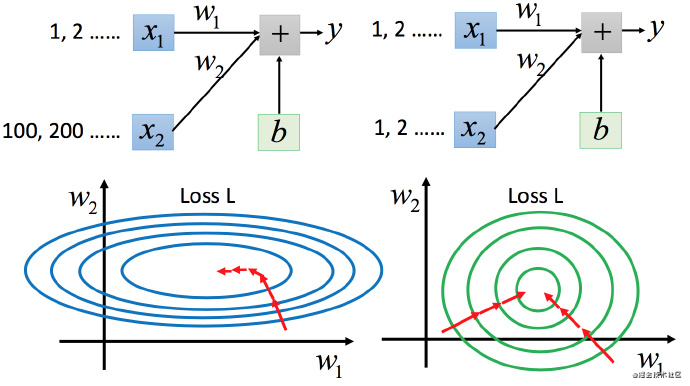
上图左边是?x1的scale比?x2?要小很多,所以当?w1和?w2做同样的变化时,w1?对?y?的变化影响是比较小的,x2对?y?的变化影响是比较大的。左边的梯度下降并不是向着最低点方向走的,而是顺着等高线切线法线方向走的。但绿色就可以向着圆心(最低点)走,这样做参数更新也是比较有效率。
如何放缩
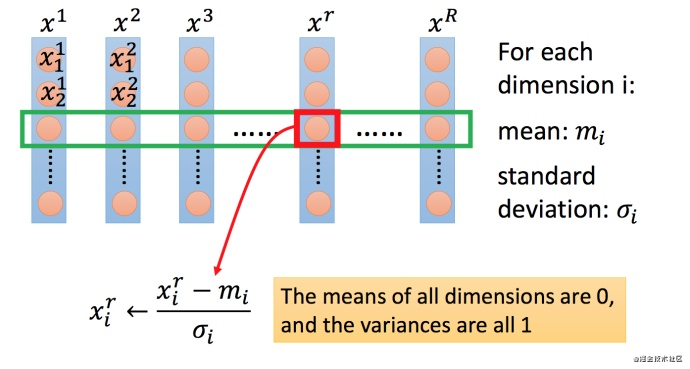
上图每一列都是一个例子,里面都有一组特征。
对每一个维度?i(绿色框)都计算平均数,记做? m i m_i mi?;还要计算标准差,记做? σ i \sigma _i σi?。
然后用第?r?个例子中的第?i?个输入,减掉平均数 ? m i ?m_i ?mi?,然后除以标准差? σ i \sigma _i σi?,得到的结果是所有的维数都是?0,所有的方差都是?1
特征缩放的几种方法:
(1)最大最小值归一化(min-max normalization): 将数值范围缩放到?[0,?1]?区间里
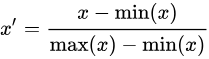
(2)均值归一化(mean normalization) :将数值范围缩放到?[-1,?1]?区间里,且数据的均值变为0
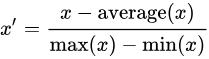
(3)标准化 /?z值归一化(standardization /z-score?normalization ) :将数值缩放到0附近,且数据的分布变为均值为0,标准差为1的标准正态分布(先减去均值来对特征进行?中心化 mean centering?处理,再除以标准差进行缩放)

(4)最大绝对值归一化(max abs?normalization ) : 也就是将数值变为单位长度(scaling to unit length) ,将数值范围缩放到?[-1,?1]?区间里
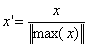
(5)稳键标准化(robust standardization):先减去中位数,再除以四分位间距(interquartile range),因为不涉及极值,因此在数据里有异常值的情况下表现比较稳健
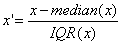
些机器学习模型必须进行特征缩放?
通过梯度下降法求解的模型需要进行特征缩放,这包括线性回归(Linear Regression)、逻辑回归(Logistic Regression)、感知机(Perceptron)、支持向量机(SVM)、神经网络(Neural Network)等模型。此外,近邻法(KNN),K均值聚类(K-Means)等需要根据数据间的距离来划分数据的算法也需要进行特征缩放。主成分分析(PCA),线性判别分析(LDA)等需要计算特征的方差的算法也会受到特征缩放的影响。
决策树(Decision Tree),随机森林(Random Forest)等基于树的分类模型不需要进行特征缩放,因为特征缩放不会改变样本在特征上的信息增益。
行特征缩放的注意事项:
需要先把数据拆分成训练集与验证集,在训练集上计算出需要的数值(如均值和标准值),对训练集数据做标准化/归一化处理(不要在整个数据集上做标准化/归一化处理,因为这样会将验证集的信息带入到训练集中,这是一个非常容易犯的错误),然后再用之前计算出的数据(如均值和标准值)对验证集数据做相同的标准化/归一化处理。
梯度下降的限制
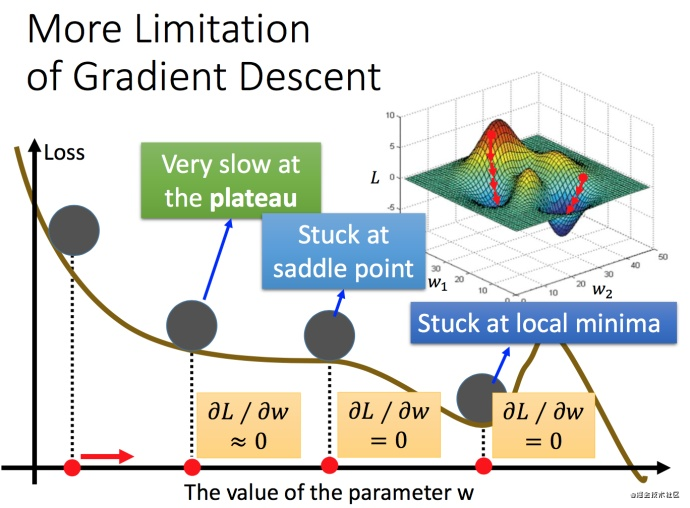
容易陷入局部极值 还有可能卡在不是极值,但微分值是0的地方 还有可能实际中只是当微分值小于某一个数值就停下来了,但这里只是比较平缓,并不是极值点,对于这个问题的解释可以看前一篇文章
参考链接:
- 链接:https://www.zhihu.com/question/27068705/answer/35151681
- 链接:https://www.zhihu.com/question/27068705
- 链接:https://segmentfault.com/a/1190000016447144
- 链接:https://www.cnblogs.com/HuZihu/p/9761161.html