error来自于什么地方
- 一个来自于bias,一个来自于variance
- 你的estimator是不是biased,判断标准
E
[
f
?
]
=
f
^
E[f^*] = \hat f
E[f?]=f^? (有没有瞄准靶心🎯)
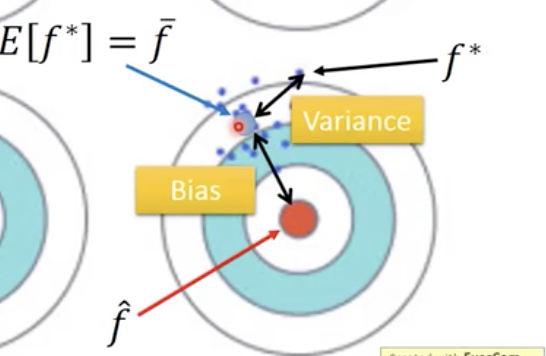 - 这样你的
f
^
\hat f
f^?与靶心之间就是有一个bias的
- 每一个
f
?
f^*
f?与
f
^
\hat f
f^?之间的距离就是一个variance
- 比较简单的model就是bias比较大,variance比较小
- 比较复杂的model就是bias比较小,variance比较大
- 如果你的error来自于bias很大,那么就是underfitting。如果你的error来自于variance很大,那么就是overfitting。
what to do with large variance
- more data:很高效,不会对bias有所影响,但是往往我们没有那么多的data
- Regularization:可能会伤害bias
- 一般select a model可以平衡这两种误差
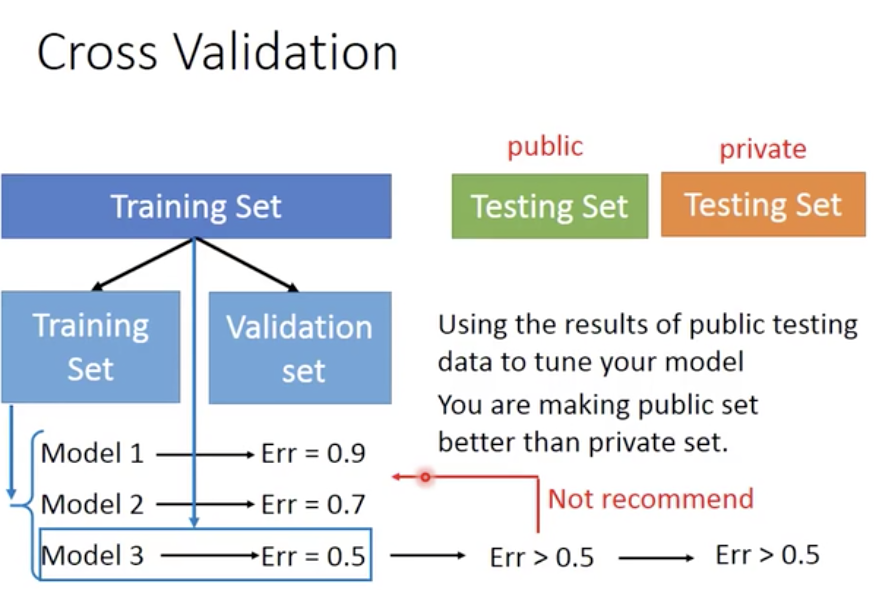 - 除了Cross Validation,还可以N-fold Cross Validation
梯度下降
Tip1: Tuning your learning rate
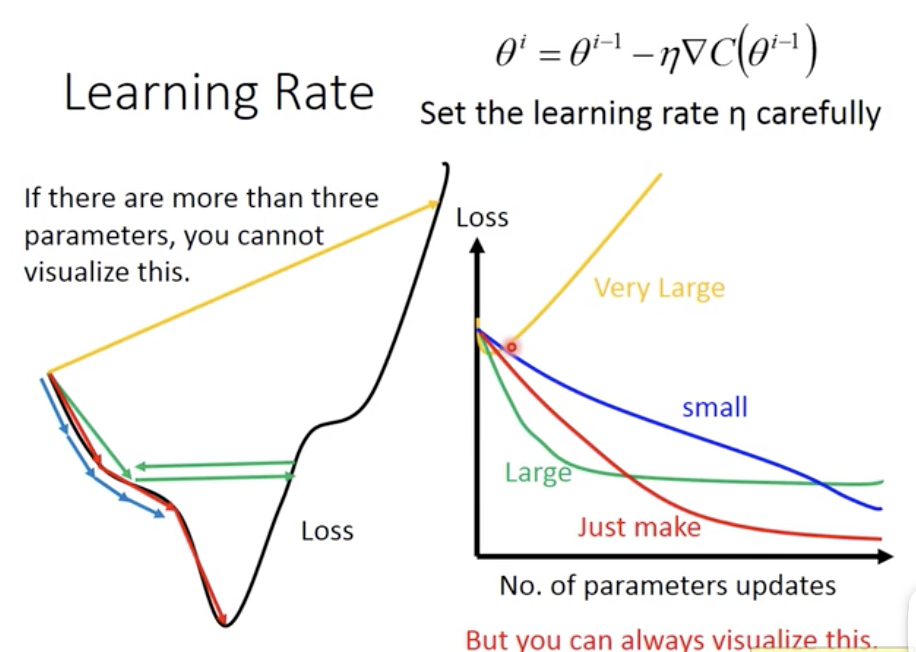
- 最好画出右边这个图,看看learning rate有没有太大或者太小
- 自动调节learning rate
一般来说一开始learning rate要设置比较大,随着epoch次数的增多,learning rate逐渐减小
比如:
η
t
=
η
/
t
+
1
\eta ^t = \eta / \sqrt{t+1}
ηt=η/t+1
? (t为迭代的次数) - 但是learning rate并不是one-size-fits-all,最好还是每一个参数都设置不同的learning rate
- 其中最好做的就是Adagrad

 - 这里是过去所有的参数微分的root mean square,不能看作上一个微分的root mean square
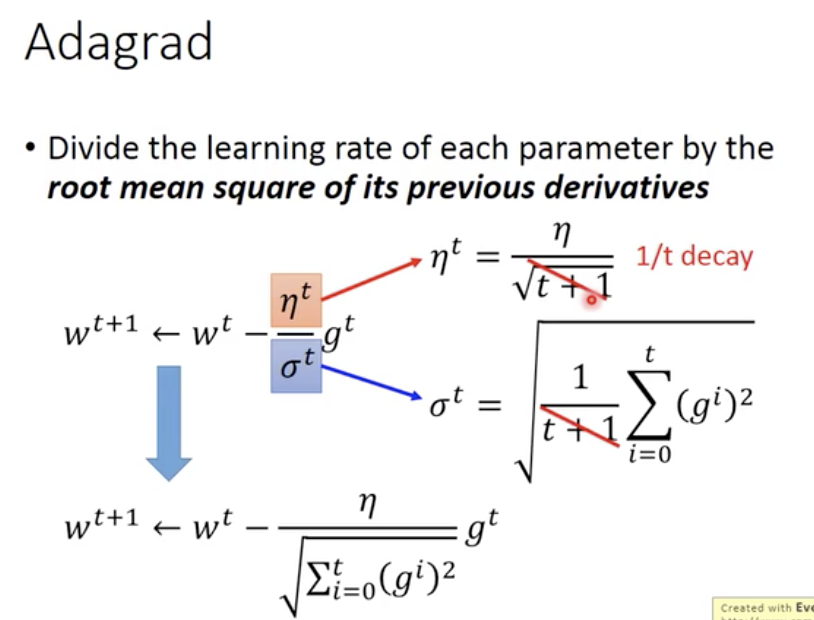 - 但在这个更新式子中,larger gradient, 在分子处是larger steps,在分母处确实smaller steps
- 在只考虑一个参数的时候,更新参数选择和微分成正比
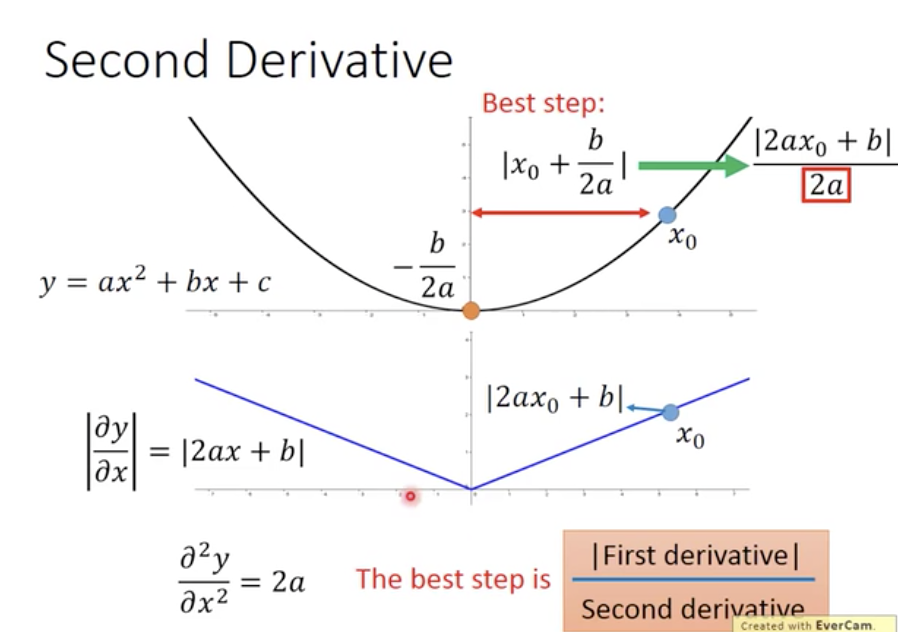 - 所以最好的更新方向应该与二次微分呈反比,与一次微分成正比。这样才能比较准确的反映这个点和最低点之间的距离
- Adagrad就类似于这里
Stochastic Gradient Descent
|






