RBF网络
一、概述
Radical Basis Function ,RBF(径向基)网络的结构与多层前向网络类似,它是一种三层前向网络。
第一层为输入层,由信号源结点组成;
第二层为隐含层,隐单元数量由所描述问题决定,隐单元的变换函数是对中心点径向对称且衰减的非负非线性函数,该函数是局部响应函数(之前的前向网络变换的函数是全局的);
第三层为输出层,它对输入模式的作用作出响应。
从输入空间到隐含层空间的变换是非线性的,而从隐含层空间的输出层空间变换是线性的。
具有n个输入的RBF神经网络结构: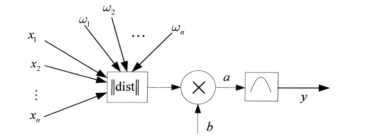
b为阈值,用于调整神经元灵敏度。RBF神经元和线性神经元可以建立广义回归神经网络,用于函数逼近方面;RBF神经元和竞争神经元可以组建概率神经网络,用于解决分类问题。
RBF网络的基本思想:用RBF作为隐单元的“基”构成隐藏层空间,隐含层对输入矢量进行变换,将低维的模式输入数据变换到高维空间内,使得在低维空间内的线性不可分的问题在高维空间内线性可分。
RBF神经网络结构简单,训练简洁而且学习收敛速度快,能够逼近任意非线性函数,因此它已被广泛应用于时间序列分析,模式识别,非线性控制和图形处理等领域。
RBF神经网络的激活函数采用距离函数,使用RBF函数作为激活函数
径向基神经网络的激励函数是以输入向量和权值向量之间的距离||dist||作为自变量,激活函数的表达式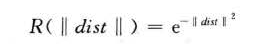
权值和输入向量距离减少,网络输出是递增的,当一致时,神经元输出为1由输入层、隐藏层和输出层构成的一般径向基神经网络结构如图。在 RBF神经网络中,输入层仅仅起到传输信号的作用,与前面所讲述的神经网络相比较,输人层和隐含层之间可以看作连接权值为1的连接,输出层和隐含层所完成的任务是不同的,因而它们的学习策略也不相同。输出层是对线性权进行调整,采用的是线性优化策略,因而学习速度较快。而隐含层是对激活函数(格林函数或高斯函数,一般取高斯函数)的参数进行调整,采用的是非线性优化策略,因而学习速度较慢。
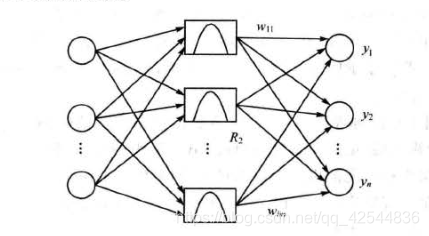
RBF神经网络的学习算法
需要求解的参数:基函数的中心,方差,隐含层到输出层的权值
学习方法:随机选取中心法、自组织选取法、有监督选取中心法和正交最小二乘法等。自组织选取中心学习法:该方法由两个阶段组成:一是自组织学习阶段,此阶段为无导师学习过程,求解隐含层基函数的中心与方差;二是有导师学习阶段,此阶段求解隐含层到输出层之间的权值。
曲线拟合:
曲线拟合(curve fitting)是用连续曲线近似地刻画或比拟平面上离散点组所表示的坐标之间函数关系的一种数据处理方法,是用解析表达式逼近离散数据的一种方法。在科学实验或社会活动中,通过实验或观测得到量工与y 的一组数据对(Xi,Yi)(i=1,2…,m),其中Xi是彼此不同的。人们希望用一类与数据的背景材料规律相适应的解析表达式如y=f(z,c)来反映量工与y之间的依赖关系,即在一定意义下“最佳”地逼近或拟合已知数据。y=f(r,c)常被称作拟合模型,式中c=(C1,C2…,Cn)是一些待定参数。当c在f中线性出现时,此时称模型f为线性模型,否则称f为非线性模型。现在有许多衡量拟合优度的标准,最常用的一种做法是选择参数c使得拟合模型与实际观测值在各点的残差(或离差)e=y一f(x,c)的加权平方和达到最小,此时所求曲线称作在加权最小二乘意义下对数据的拟合曲线。目前有许多求解拟合曲线的成功方法,对于线性模型一般通过建立和求解方程组来确定参数,从而求得拟合曲线。至于非线性模型,则要借助求解非线性方程组或用最优化方法求得所需参数才能得到拟合曲线,有时也称之为非线性最小二乘拟合。
RBF网络的相关函数
1、newrb() 设计一个近似径向基网络
[net,tr]=newrb(P,T,GOAL,SPREAD,MN,DF)
其中,P为Q组输人向量组成的RQ维矩阵;T为Q组目标分类向量组成的SQ维矩阵;GOAL为均方误差目标(Mean Squared Error Goal),默认为0.0;SPREAD为径向基函数的扩展速度,默认为1;MN为神经元的最大数目,默认为Q;DF为两次显示之间所添加的神经元数目﹐默认为25 ; net为返回值,一个 RBF网络;tr为返回值,训练记录。