前言

论文地址： https://arxiv.org/pdf/1710.05941.pdf.

Swish的优点有：

1.无上界（避免过拟合）
2. 有下界（产生更强的正则化效果）
3. 平滑（处处可导更容易训练）
4. x<0具有非单调性（对分布有重要意义这点也是Swish和ReLU的最大区别）。

一、背景

$\qquad$ 在深度神经网络中选择合适的激活函数对网络的动态训练和任务的性能具有显著的影响。因为每个深度神经网络的核心都是进行线性变换，然后紧接一个激活函数 $f(\cdot)$ ，激活函数在训练神经网络的过程中扮演着非常重要的角色。

$\qquad$ 现在最受欢迎被大家广泛接受的激活函数是修正线性单元 Rectified Linear Unit (ReLU) 激活函数。使用 ReLU激活函数的网络一般会比使用 Sigmoid 活着 Tanh的网络更容易优化，因为当输入x为正时，梯度是线性的。而且因为 ReLU 函数的简单性和高效性，我们常常把ReLU激活函数当成一个默认的激活函数用在我们的神经网络训练过程中。

$\qquad$ 但是今年来，也有人不断的尝试手动设计一些激活函数，虽然这些激活函数在某些特定的模型或者特定的数据集当中取得了不错的效果，但是仍然无法手动找到一个可以像ReLU激活函数那样可以在广泛的数据集或者模型当中取得不错效果的激活函数。

$\qquad$ 而我们的这次的工作就是使用自动搜索技术自动的搜索最佳的激活函数（多个一元或者二元函数组合）。

二、方法：自动搜索技术

$\qquad$ 这里的自动搜索技术就是一个类似NAS的自动搜索最佳匹配方案的一个搜索技术。将一些一元和二元函数组合在一起组成一个搜索空间，这个搜索空间的设计最大的挑战就是要同时考虑效率和性能，所以我们尽量的将一些简单的一元函数或者二元函数组合成一个简单的搜索空间。用到的一元函数和二元函数如下：
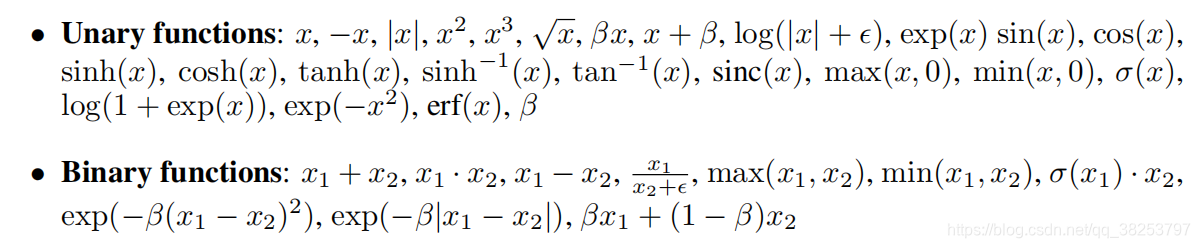
在这里插入图片描述
$\qquad$ 具体的搜索技术我就不再介绍了，因为这个不是本文的重点，而且还需要极大的算力资源。我们直接说搜索结果好了。

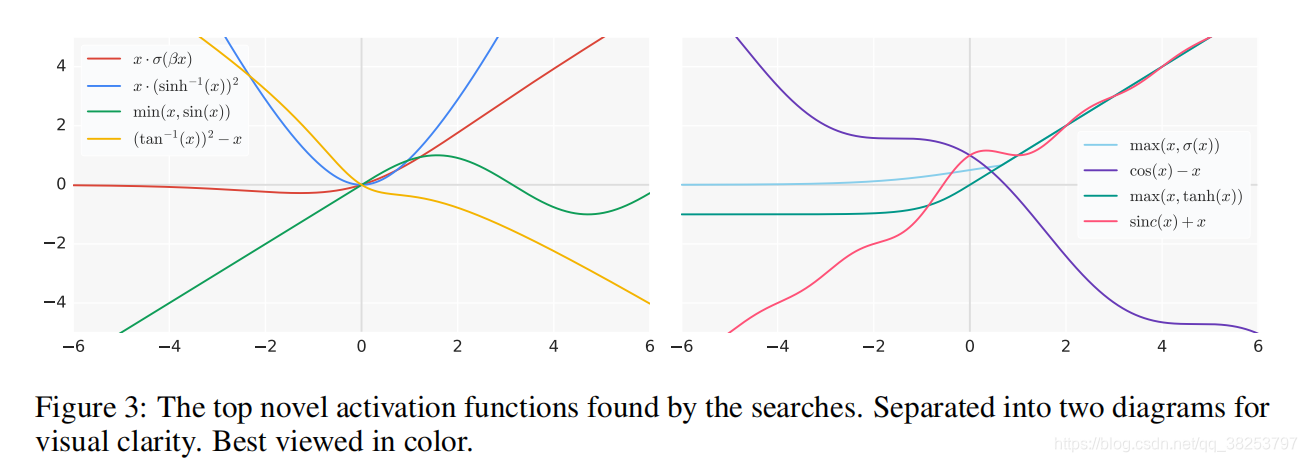
$\qquad$ 如上图，是我们搜索到的一些效果不错的一些激活函数，纵观这些函数，我们可以总结以下几点发现（设计激活函数的准则）:

复杂的激活函数性能始终要低于简单的激活函数的性能。可能是因为复杂的激活函数优化难度增加。最好的激活函数一般都是由一到两个核心单元组成。
一般使用原始预激活x（raw preactivation x）作为最终的二元函数的输入效果会比较好。
使用除法的效果一般都会比较差，因为一旦分母趋于0时输出就会爆炸（梯度爆炸）。
常常会使用一些周期函数（periodic functions），如 sin 或 cos等。

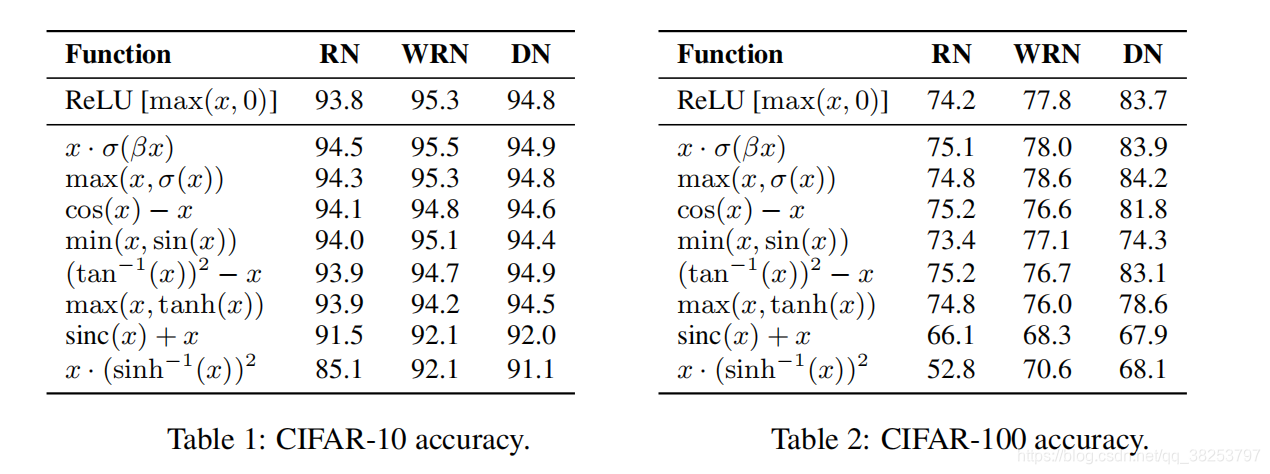
$\qquad$ 为了验证这些激活函数的普适性，在这之后作者又在很多模型和数据集上做了实验，如下图，发现只有激活函数 $\cdot \sigma(\beta x)$ 和 $\sigma(x))$ 的性能在众多的模型和函数中都表现的优于ReLU激活函数，而且 $\cdot \sigma(\beta x)$ 的性能优于 $\sigma(x))$ 。所以我们下面再对 $S w i s h (x)$ 激活函数作进一步的分析。

在这里插入图片描述

三、Swish 激活函数

公式: $\cdot \sigma(\beta x) = x \cdot \frac{1}{1 + e^{-\beta x}}$ ，其中 $\beta$ 是一个常数或者可训练的参数

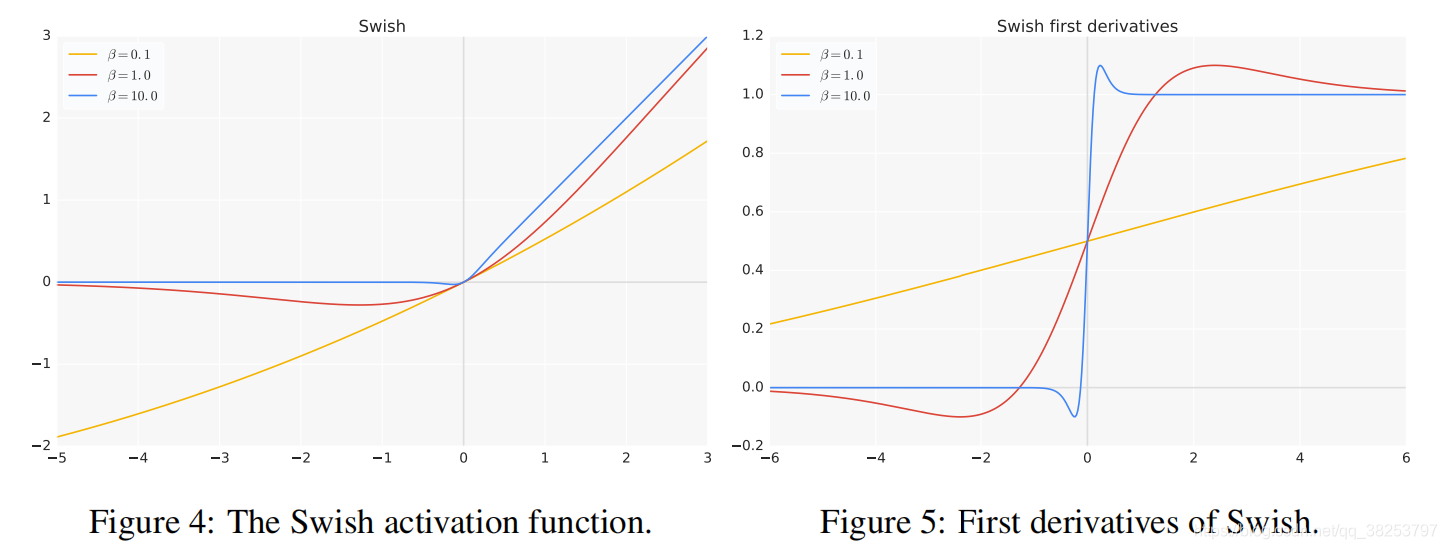
在这里插入图片描述

如上图为不同参数下的 $S w i s h (x)$ 函数，可以看到：

当 $\beta=1$ 时，则Swish等效于Elfwing等人的Sigmoid加权线性单元（SiL），其被提议用于强化学习。
当 $\beta=0$ 时，则Swish变为缩放线性函数 $\frac{x}{2}$ 。
当 $\beta->\infty$ 时，sigmoid组件变成接近0-1函数，因此Swish变得像ReLU一样的函数。

总结：由此可见 $S w i s h (x)$ 函数是介于线性函数和 ReLU 函数之间进行线性插值的函数，而参数 $\beta$ 则控制插值的程度。

而且从图中也可以看出：

和ReLU函数一样，Swish函数也是一个无上界（避免梯度饱和）有下界（产生更强的正则化效果）的函数。
和ReLU函数不一样的是，Swish函数还是一个平滑（处处可导更易训练）且非单调（很重要）的函数。
?

当 x>0 时，通过对函数求一阶导可知：

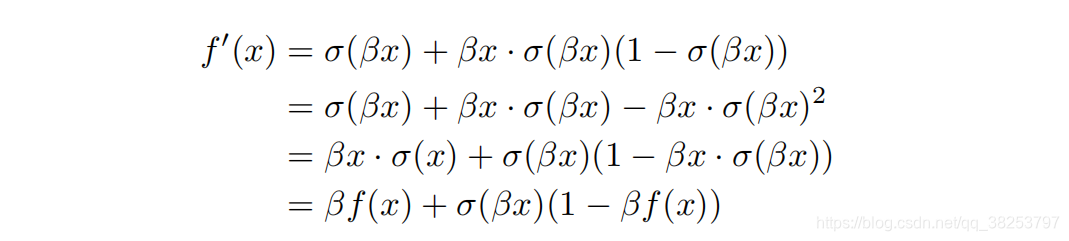
在这里插入图片描述
$\qquad$ 当 $\beta=1$ 时， Swish函数具有同ReLU函数一样的性质：梯度保持性（平滑性），即当x>0时，处处可导（这点从上面的一阶导数函数图也可以看出来）。这可以证明直接取 $\beta=1$ 这是有效的（实践中也通常是取1，证明是有效果的），但是 $\beta$ 的最佳效果并不一定是取1。

当x<0 时，由下图也可以看出函数的大部分都落在了区间（-5，0）之间，且呈峰形分布（不单调），这也可以表面Swish函数的非单调性是一个很重要的性质。
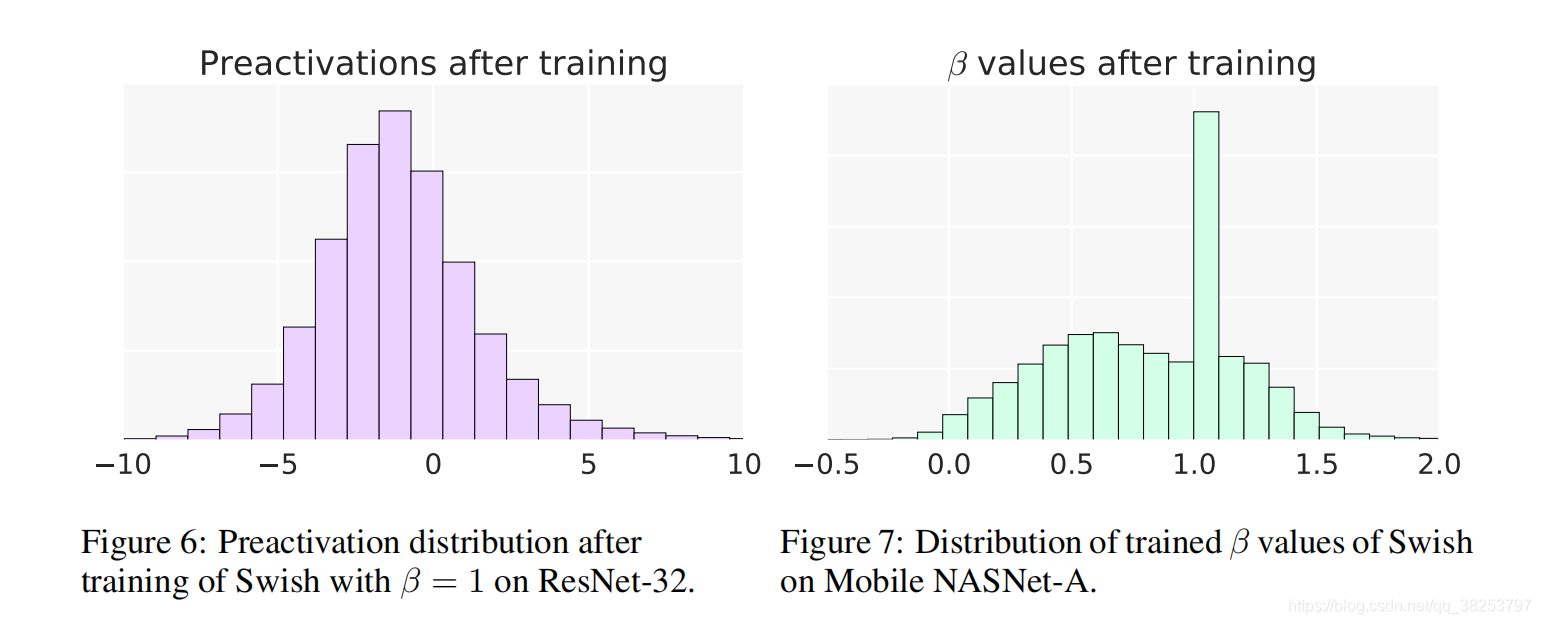
在这里插入图片描述
在实验过程（代码）中，我们一般都是直接令 $\beta=1$ 的。

$\qquad$ 最后，整理下Swish的优点有：无上界（避免过拟合）、有下界（产生更强的正则化效果）、平滑（处处可导更容易训练）、x<0具有非单调性（对分布有重要意义这点也是Swish和ReLU的最大区别）。

四、PyTorch实现

普通的Swish：

class SiLU(nn.Module): 
    # SiLU/Swish
    # https://arxiv.org/pdf/1606.08415.pdf
    @staticmethod
    def forward(x):
        return x * torch.sigmoid(x)  # 默认参数 = 1

还有一种更高效的Swish实现方式：

class MemoryEfficientSwish(nn.Module):
    # 节省内存的Swish 不采用自动求导(自己写前向传播和反向传播) 更高效
    class F(torch.autograd.Function):
        @staticmethod
        def forward(ctx, x):
            # save_for_backward会保留x的全部信息(一个完整的外挂Autograd Function的Variable),
            # 并提供避免in-place操作导致的input在backward被修改的情况.
            # in-place操作指不通过中间变量计算的变量间的操作。
            ctx.save_for_backward(x)
            return x * torch.sigmoid(x)

        @staticmethod
        def backward(ctx, grad_output):
            # 此处saved_tensors[0] 作用同上文 save_for_backward
            x = ctx.saved_tensors[0]
            sx = torch.sigmoid(x)
            # 返回该激活函数求导之后的结果 求导过程见上文
            return grad_output * (sx * (1 + x * (1 - sx)))

    def forward(self, x): # 应用前向传播方法
        return self.F.apply(x)

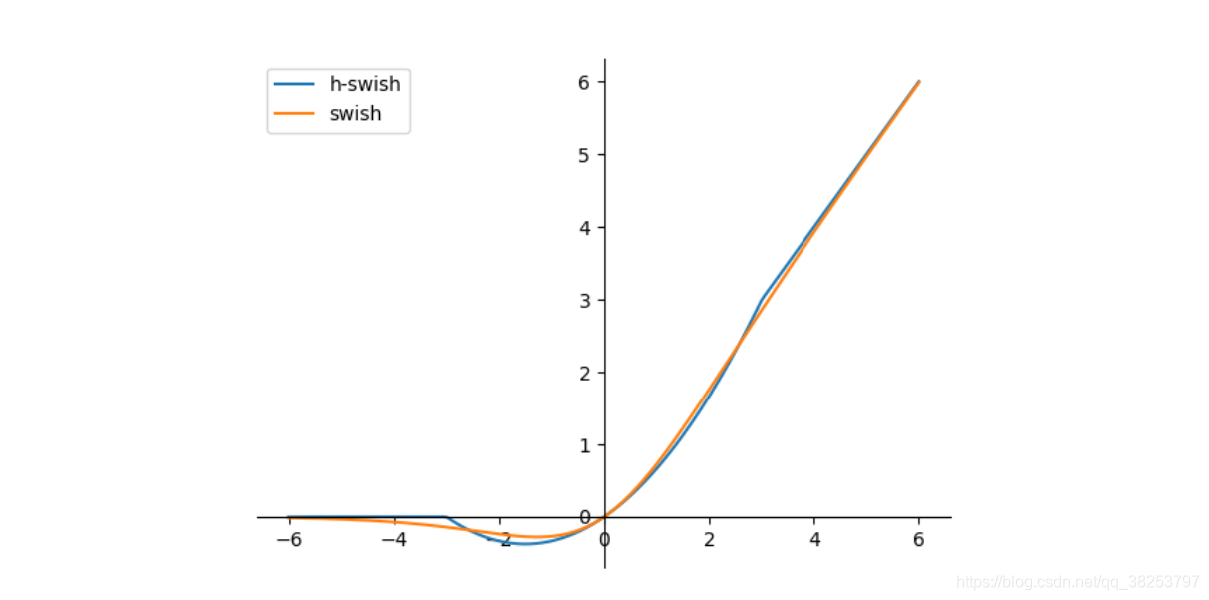
另外还有一种和Swish函数很像的函数：hard-swish

公式： $\cdot \frac{ReLU6(x+3)}{6} = x \cdot \frac{min(max(0, x+3), 6)}{6}$
在这里插入图片描述

class Hardswish(nn.Module):
    """
    hard-swish 在mobilenet v3中提出
    https://arxiv.org/pdf/1905.02244.pdf
    """
    @staticmethod
    def forward(x):
        # return x * F.hardsigmoid(x)  # for torchscript and CoreML
        return x * F.hardtanh(x + 3, 0., 6.) / 6.  # for torchscript, CoreML and ONNX