李宏毅深度学习-网络设计的技巧
本篇文章主要基于以下资料:
开源文档:课程开源文档
视频地址:B站开源视频
一、当optimization失败怎么办
在用梯度下降法优化参数时,当除最优值之外的某个点的梯度接近于0,得到的估计参数误差会比较大。这个点可能是local minima,也有可能是saddle point,其中saddle point是有方向改进的,因此我们需要区分是哪一种情形。
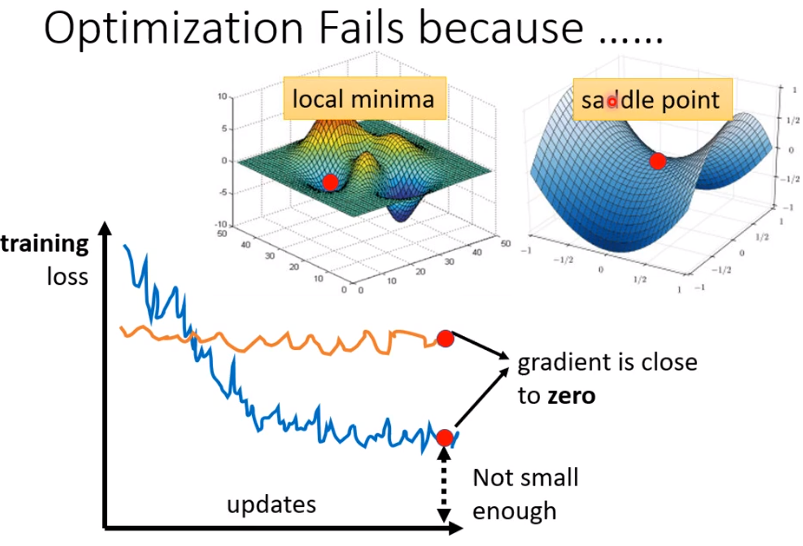
- 判断是local minimum 还是saddle point

结合泰勒展开式,当梯度趋近于0时,绿框里的值就等于0,此时如果H矩阵是正定矩阵,那么红框里的值始终大于0,此时的损失函数值是局部最小的,也就是遇到了local minima;如果H矩阵是负定矩阵,那么红框里的值始终小于0,不管往哪个方向迭代,损失函数都在减小;如果H矩阵既不是正定也不是负定,就是saddle point。而H矩阵的正定与否可以根据特征根的正负来判断。
下面的例子就展示w1=0,w2=0的点是saddle point,而不是local minima。
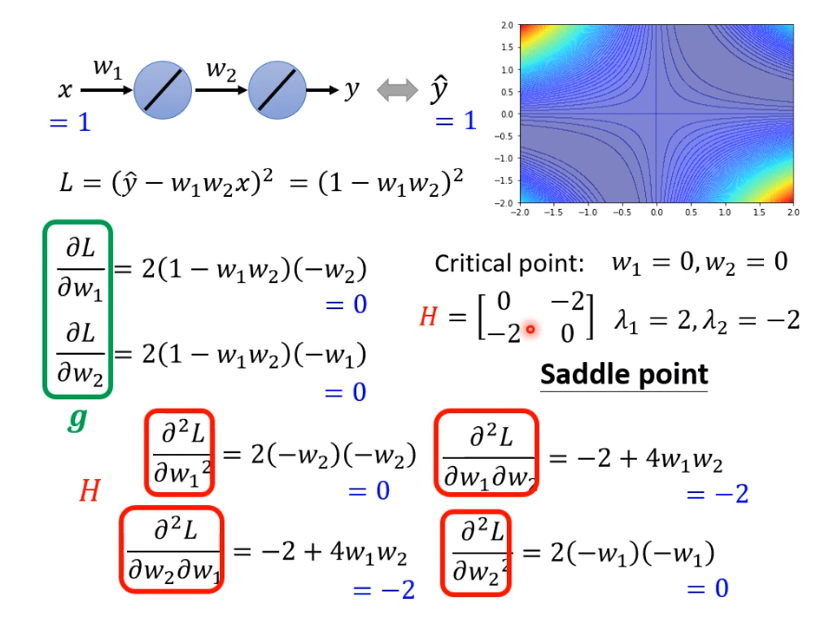
如果判断出该点是saddle point,我们可以先找到H矩阵的负值特征根对应的特征向量u,往该方向可以减小损失函数,具体原理如下图所示,但是通常我们并不用这种方法继续迭代,因为得到H矩阵以及特征根特征向量的计算量非常的大。

- saddle point VS local minima
- 从高维角度来看local minima,或许就是一个saddle point
二、 batch and momentum
1.batch
在进行参数优化迭代时,不全部用到所有的样本数据,每一次迭代用到的样本量为batch size,所有的样本数据都完成一次迭代,就是1 epoch.
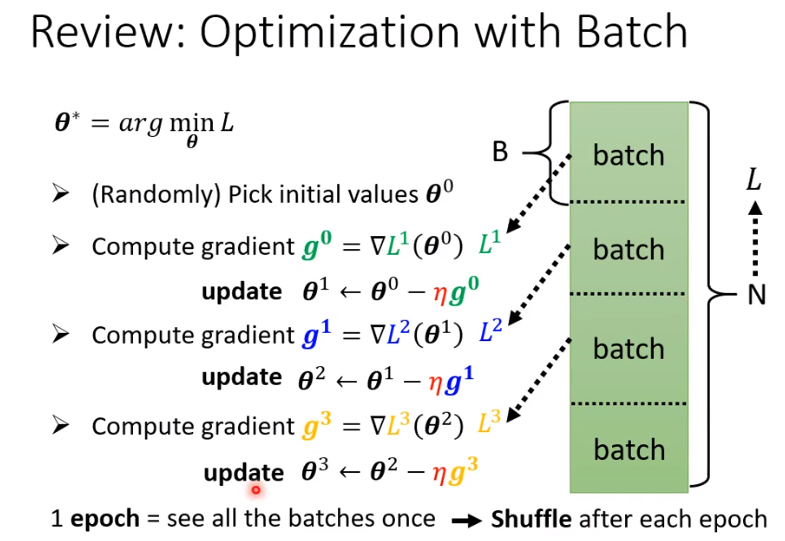
- 为什么用batch

考虑时间:larger batch的时间未必很长,除非batch size非常的大,那么时间就有个跃升。
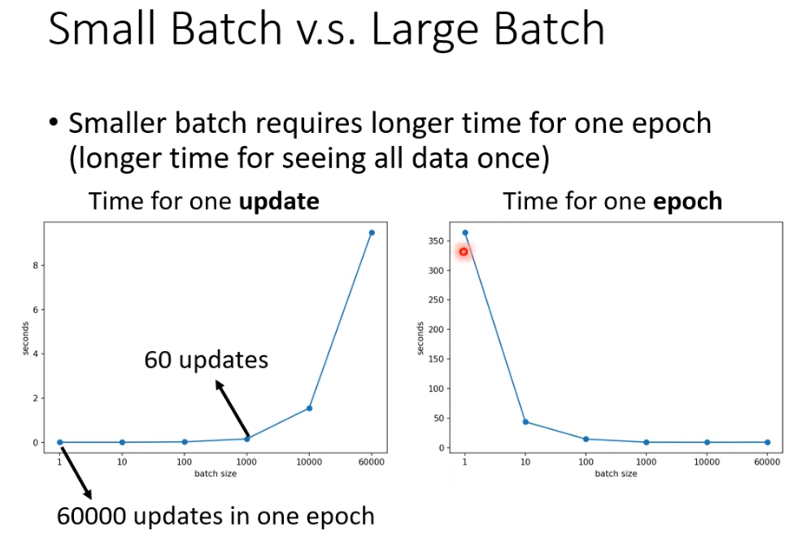
batch size越小,训练集的准确率越大,当batch size很大时,准确率下降很多。
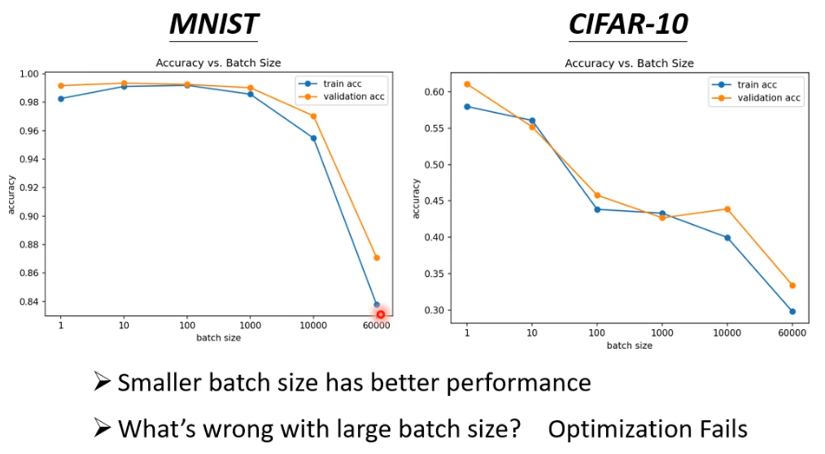
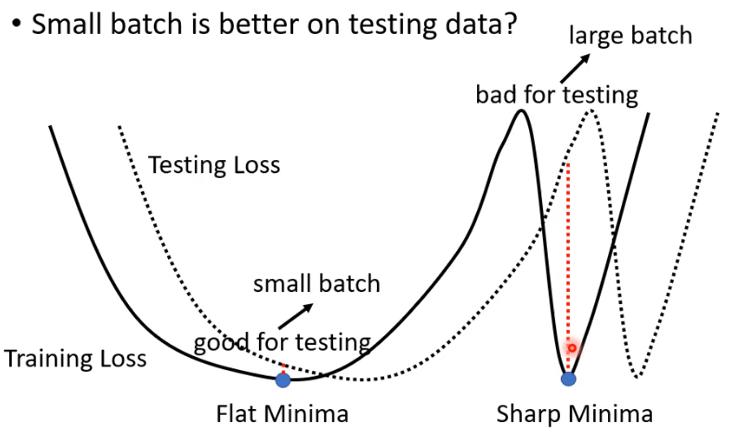
采取一定的手段,使得large batch size 和small batch size两种情形下得到的训练集准确率相同,但是batch size越小,预测效果越好
总结与对比:
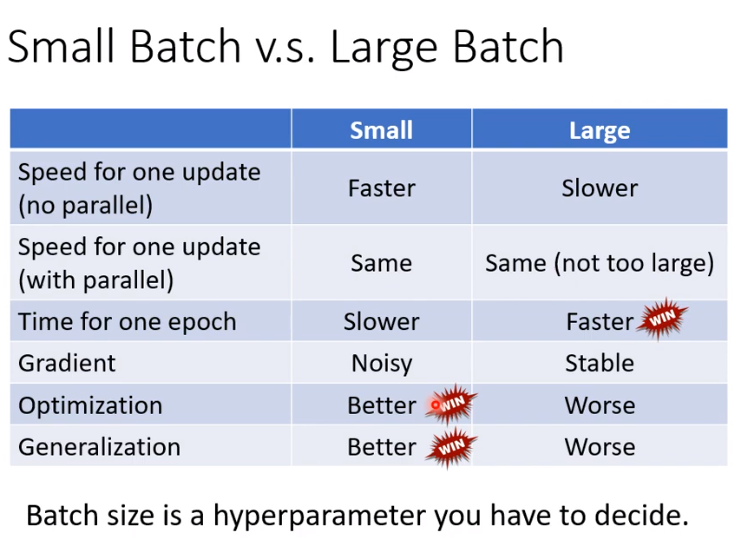
- 从物理动量的角度思考
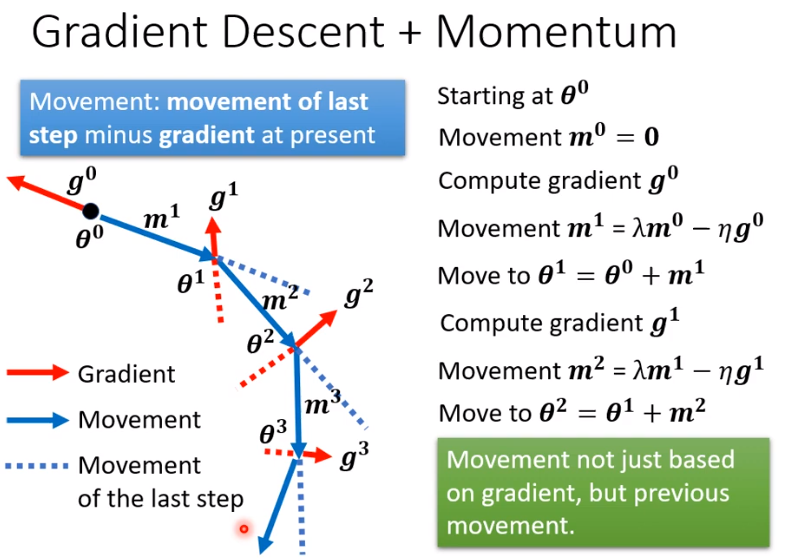
参数迭代的方向并不完全由gradient决定,由梯度和momentum共同决定
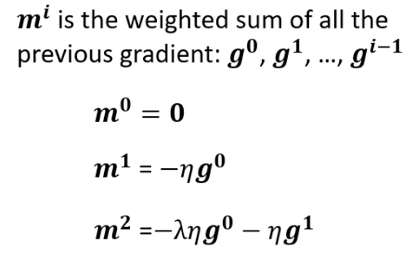
三、自动调整学习率
实际上,我们遇到的很多training stuck 都不一定是因为small gradient导致的。

如上图所示例子,当学习率为0.01时,迭代一直在两端震荡,始终没有办法接近global minima,当减小学习率到10^-7时,参数进入了平缓区但是由于学习率过于小,即使迭代100000次仍然没办法到达global minima。因此我们希望学习率更具多样化,在不同情形下取不同的值。也就是满足下面这个形式。
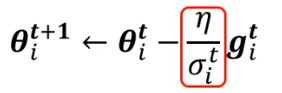
- root mean square
实现坡度大时学习率小,坡度小的时候学习率大。
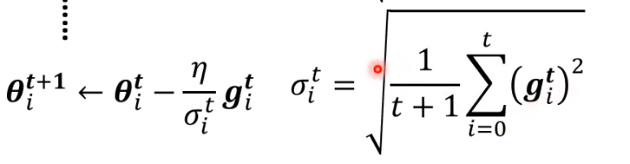
同样上面的例子使用root mean square可以得到右边的迭代图,可以发现确实参数更加接近global minima,但是在越趋近的时候就开始出现动荡。
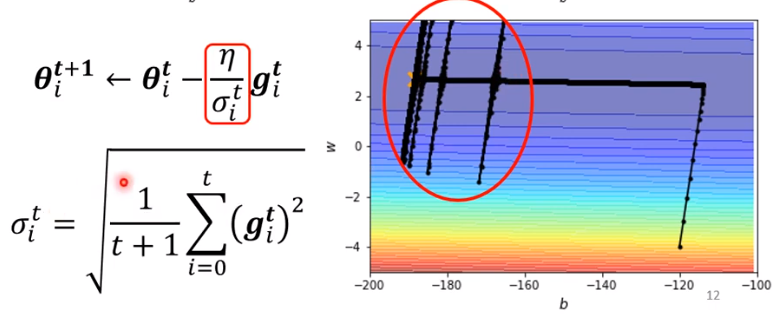
为了解决这个问题,我们又引入了learning rate scheduling,其实就是让学习率随着迭代次数也发生迭代。
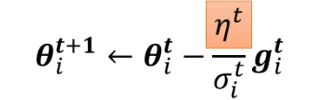
- learning rate decay
随着参数的不断迭代,我们令学习率越来越小。
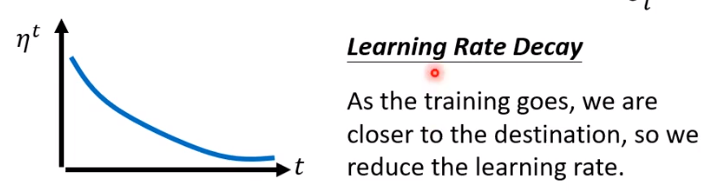
- **warm up **
这部分内容在part 7 的32分钟左右,还需要对相关材料进行研究。
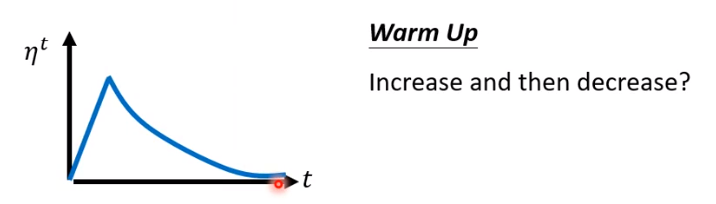
- learning rate decay
- RMS Prop
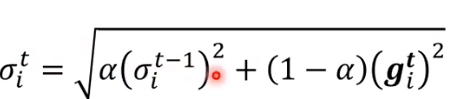
跟root mean square方法最大的区别是,该方法对邻近的点的权重更大,邻近的点的影响力更强,这也就导致学习率变化更敏感更快。 - Adam (目前最常用的优化方法)

还需要自己进一步了解扩充这个部分。 - 总结
