先吐槽一下,这个task名不大对,这五个视频明明讲的是炼丹2333。围绕着使Loss到达全局最优的目标,从梯度下降、学习率、batch、归一化等等角度阐述炼丹的经验。
【01】临界点
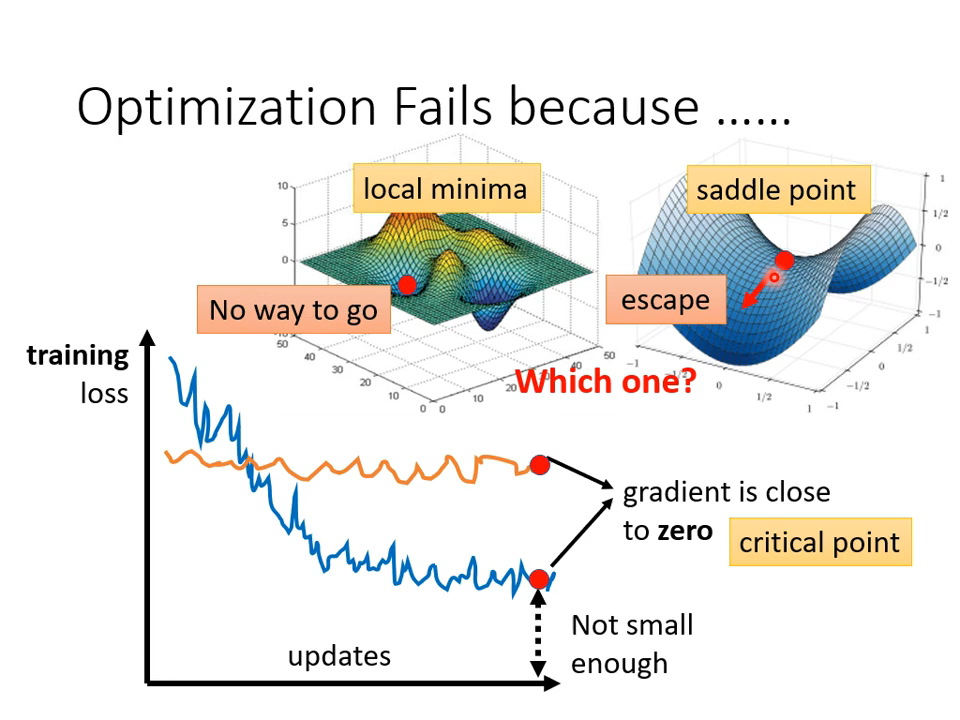
Loss如果没有到达全局最优点,就一定是到了局部最优吗?未必——
这个很好理解,就像
y
=
x
3
y = x^3
y=x3在
x
=
0
x=0
x=0处导数为0,但此时的
y
y
y并不是最小值甚至都不是极小值。放到机器学习里来,很明显这样的鞍点是不能接受的,因为还有可优化的空间。
01 如何区分?
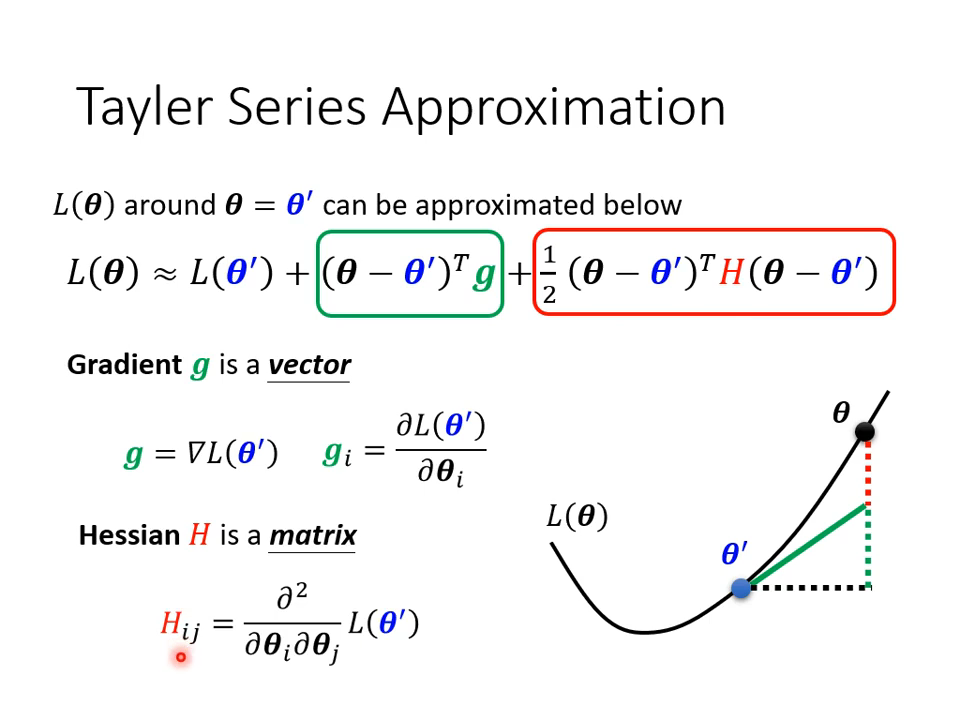
这就要用到神奇的泰勒展开了——一次偏导为0了,二次偏导可未必啊,包含着更多的信息。
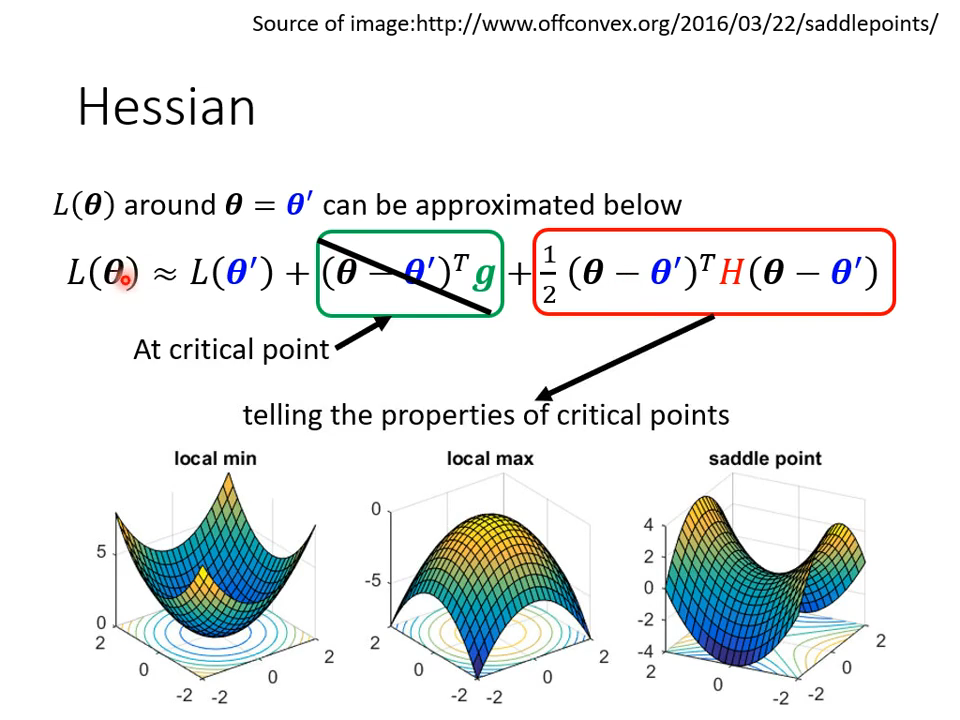

根据上面的推导,可以通过H矩阵的正定性来区分一个点是鞍点还是局部最优点。
02 如何解决鞍点?

关键还是这个二次偏导矩阵H,根据上面的推导,其实可以给出参数的更新方式,来找到新的使Loss下降的路径。
03 一些启发
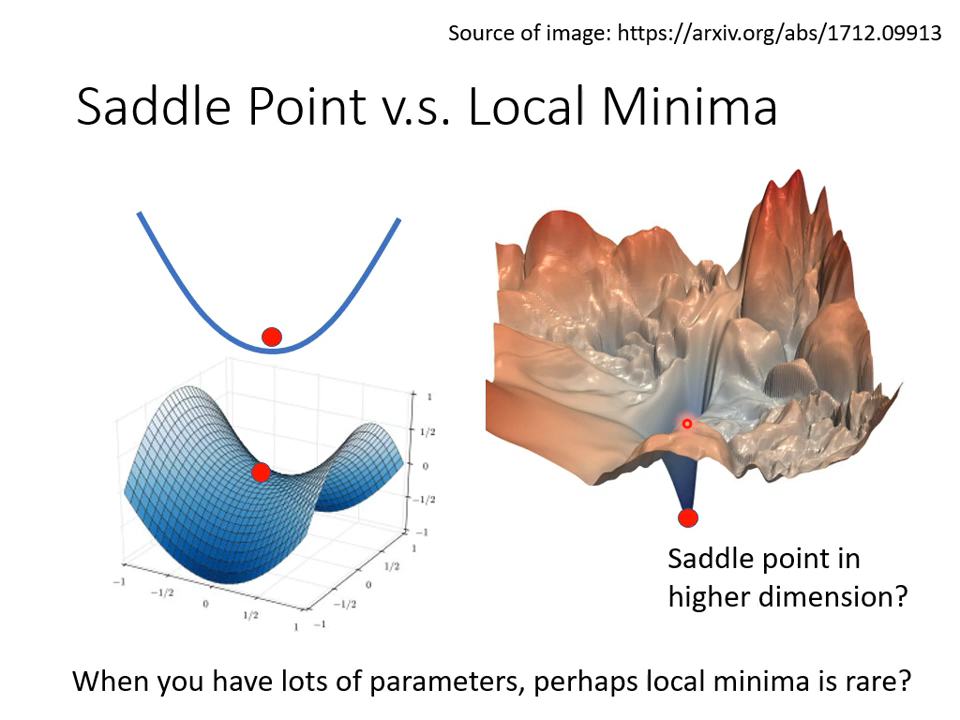
在二维是局部最优点放到三维空间里就未必了,同样的,在低维空间里的局部最优,高维空间里未必是。想象不能抵达的边界,数学依然稳定,继续用更高次的偏导矩阵去计算就行。
【02】批次
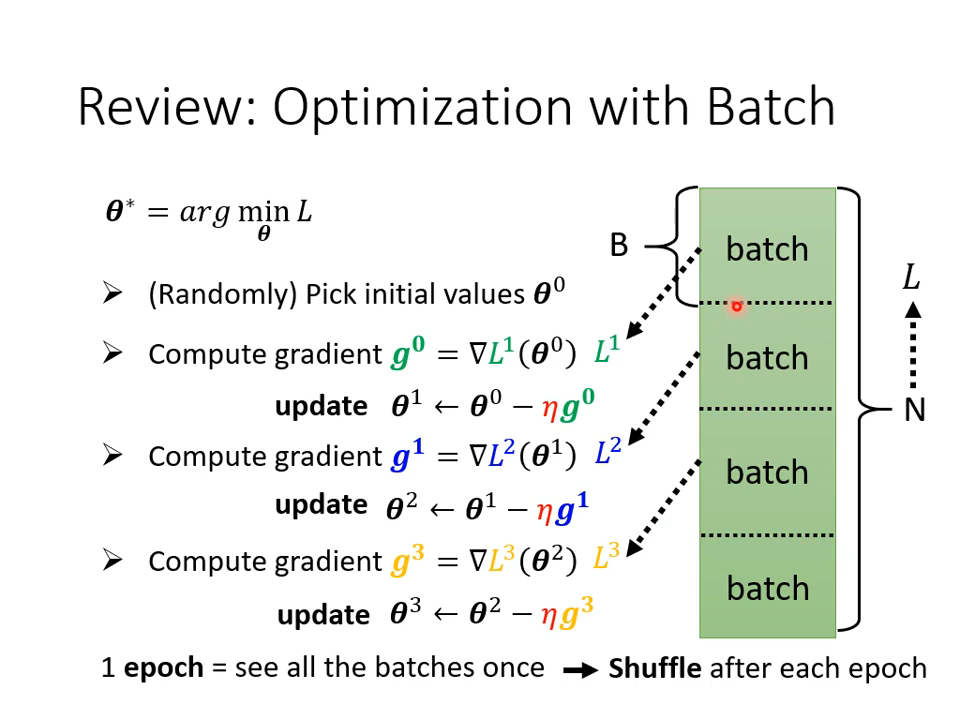
往往在做机器学习和深度学习的时候,并不是拿全部的样本去做梯度下降,而是把训练集切割成等量的小批次。那么,批次的大小(batch size)对抵达最优点有什么影响呢?
01 直觉而言

大的花时间更长,但是直接。小的更快,但是噪声多。
02 然而……
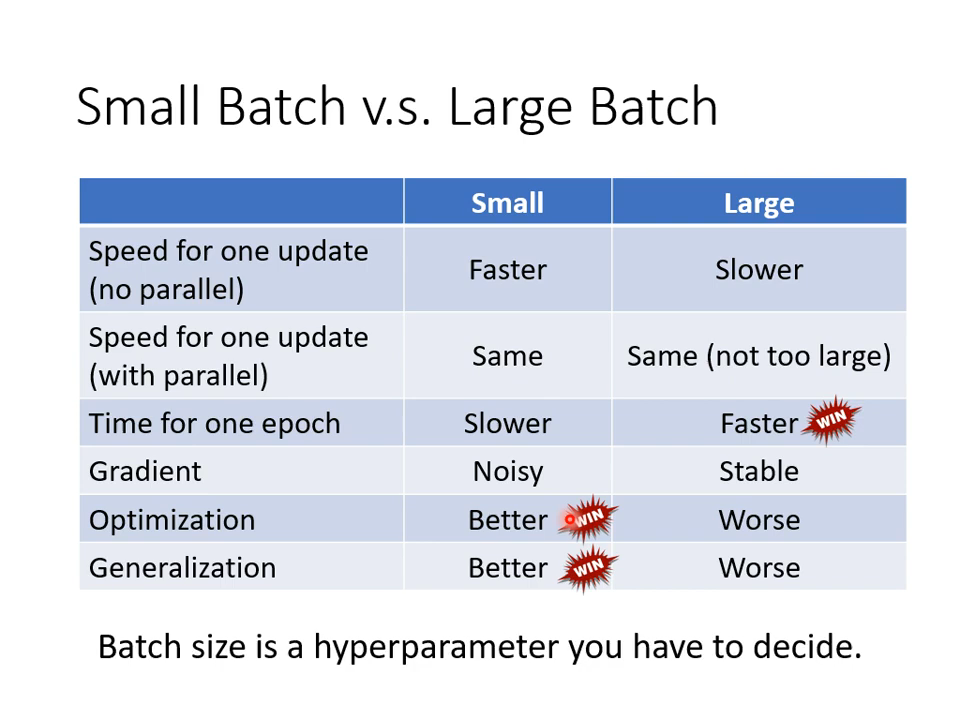
直接给出结果图吧,挺反直觉的。
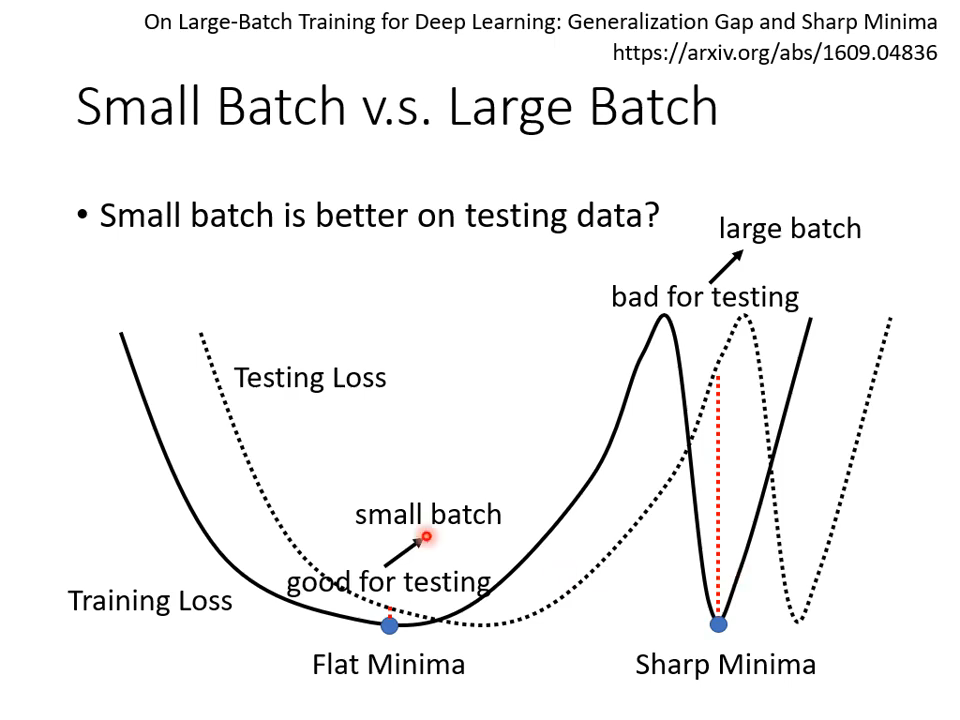
batch size更小,反而效果更好,以上是一种解释。
03 鱼与熊掌兼得?

【03】动量
对梯度下降的优化,最大的好处是可以冲过stuck
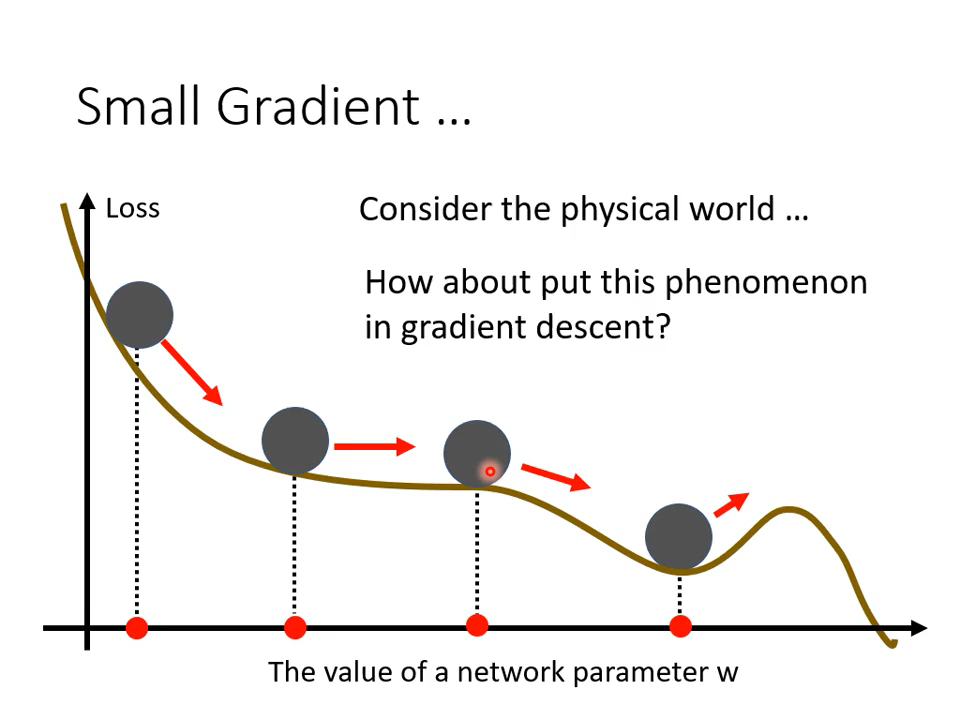
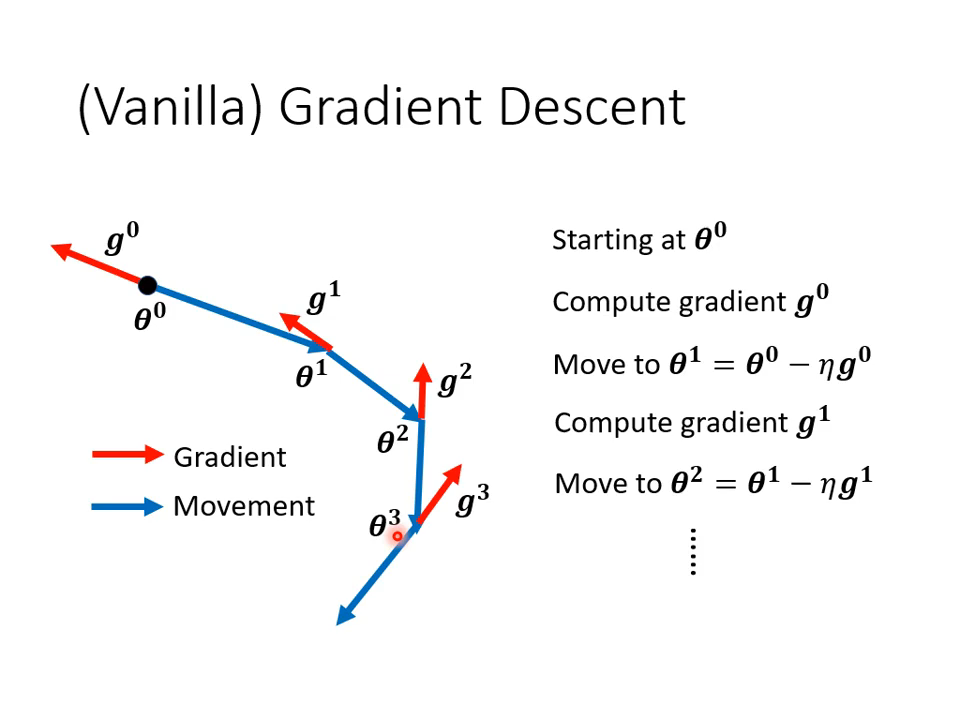
普通的梯度下降只会考虑这次计算出来的梯度,并以此作为更新参数的指导。
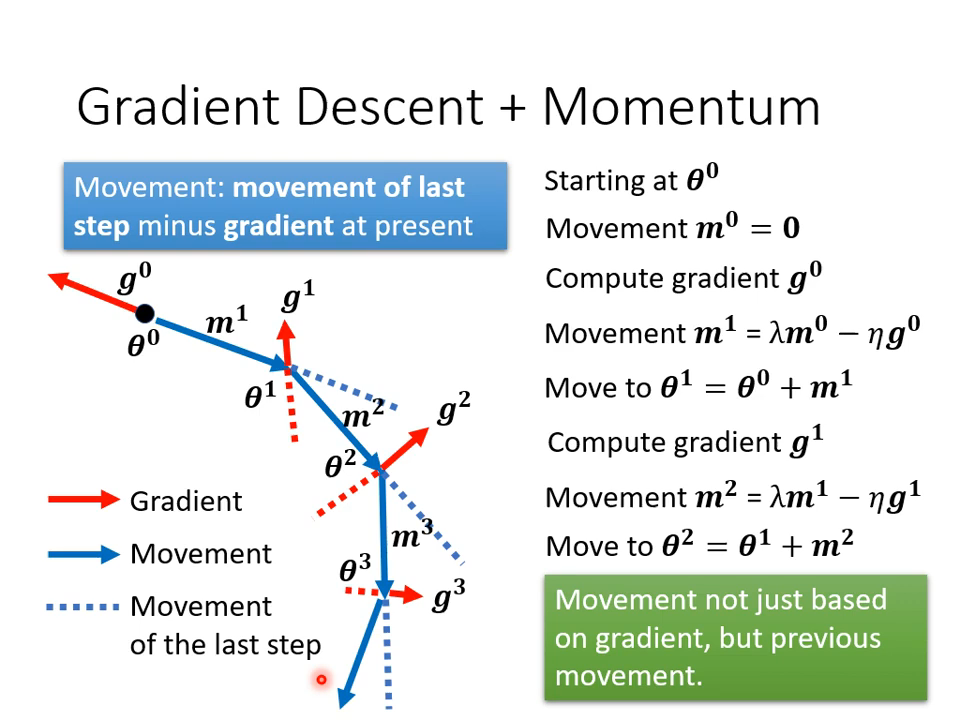
带动量的梯度下降,会考虑到上一次的更新方向——其实包含了之前所有的方向。
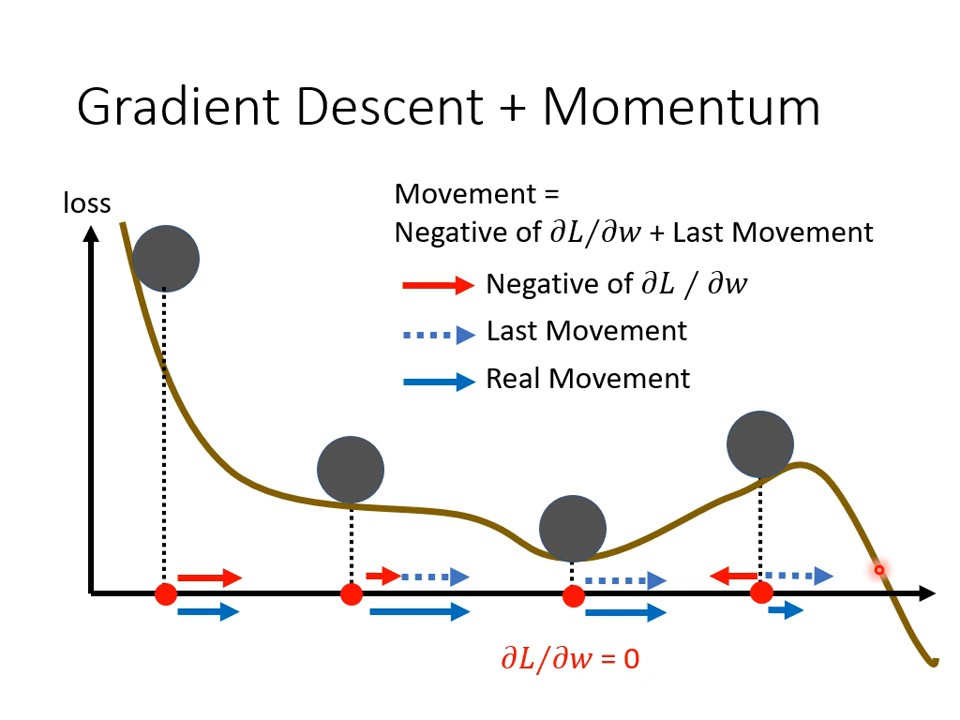
直观效果如上图。
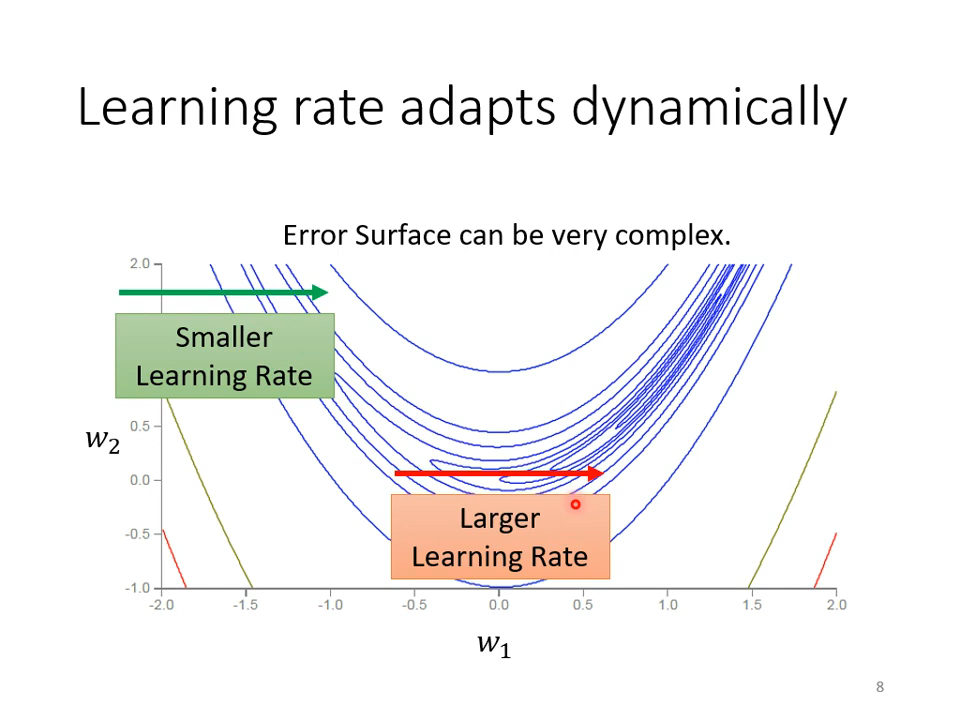
【04】自适应学习率
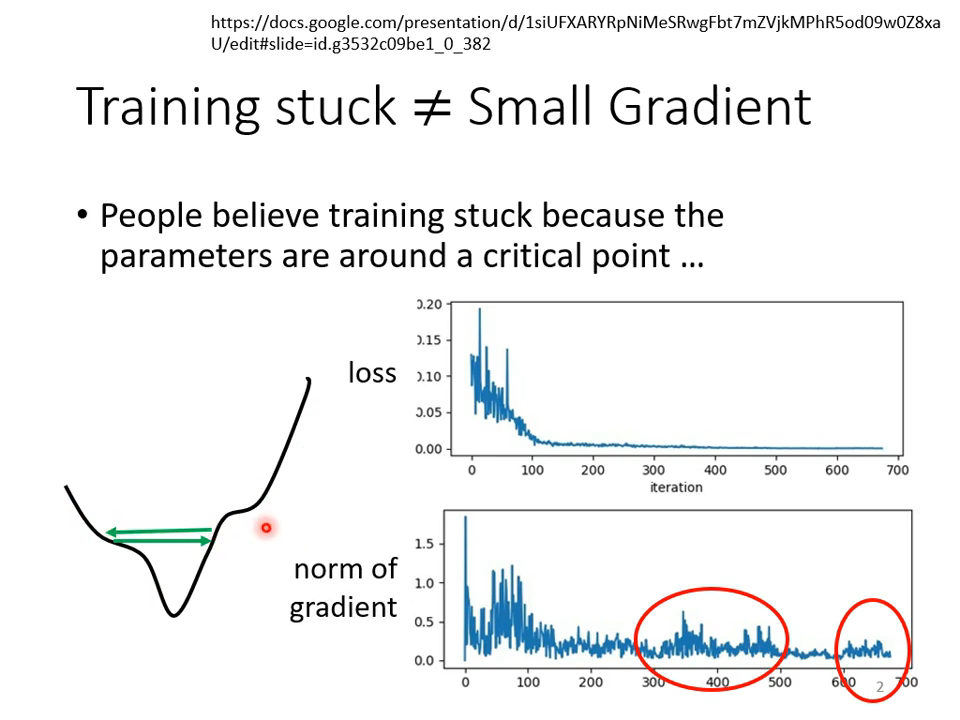
上面讨论的临界点,很多时候达不到。
灵魂发问:loss不动的时候,gradient真的很小了吗?从来没关注过!
01 what and why?
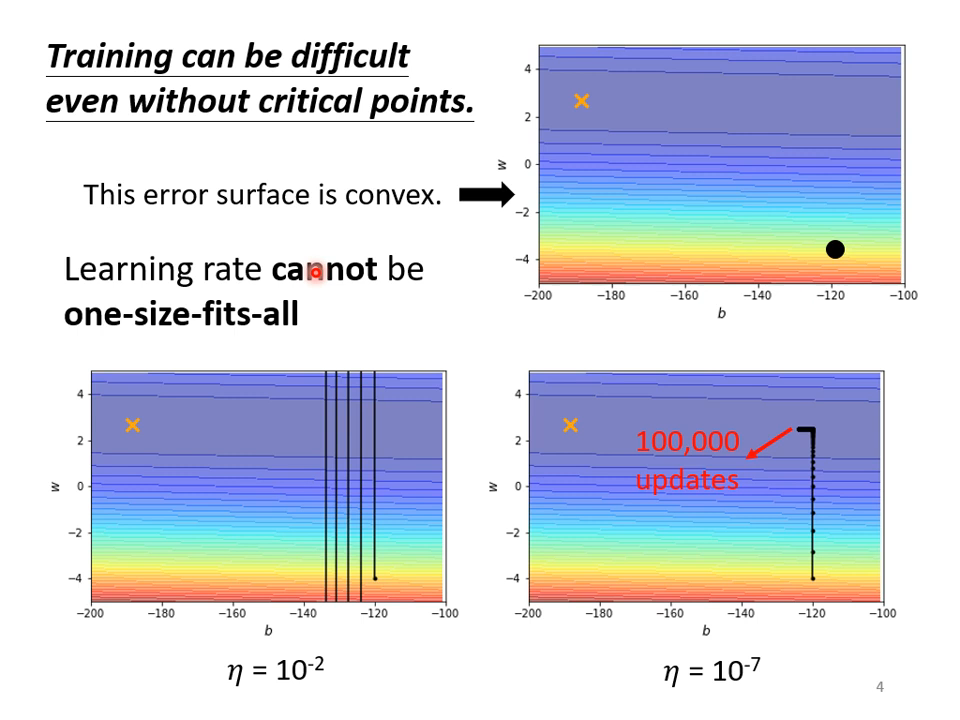
最简单的只有两个参数的神经网络,使用梯度下降也不一定能到达最优点。
02 怎么解决?
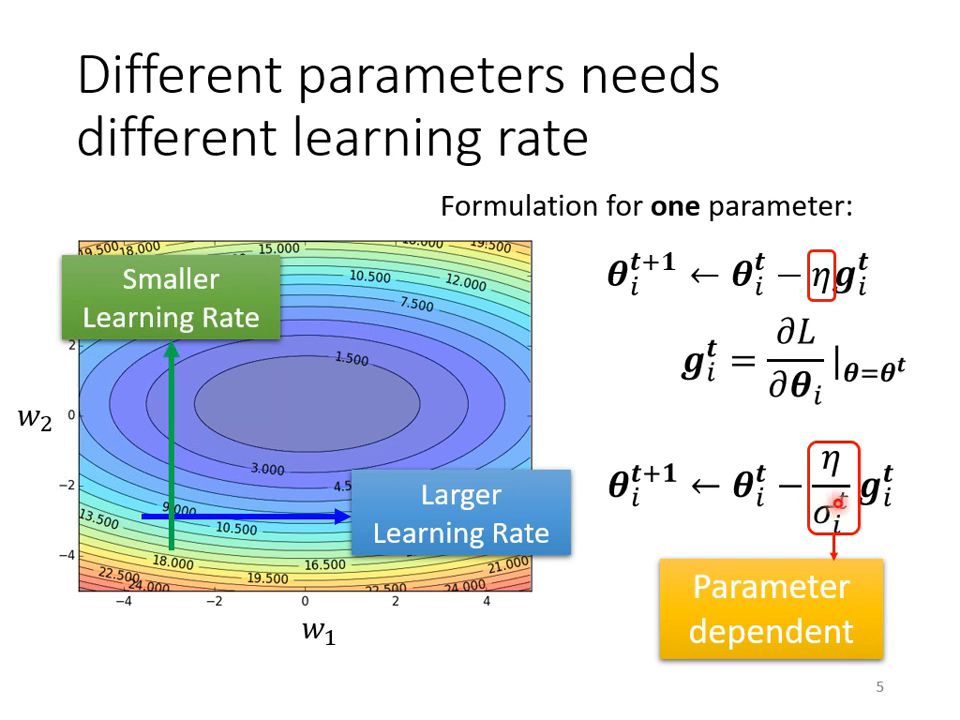
不同参数需要不同的学习率,去适应不同参数的scale(归一化不行吗?)
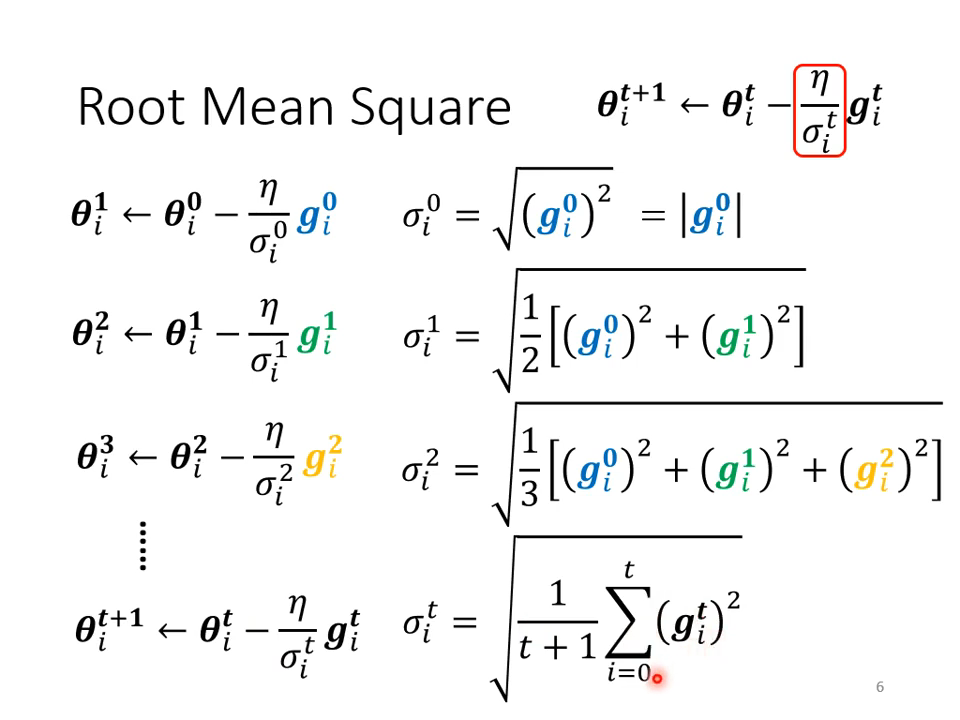
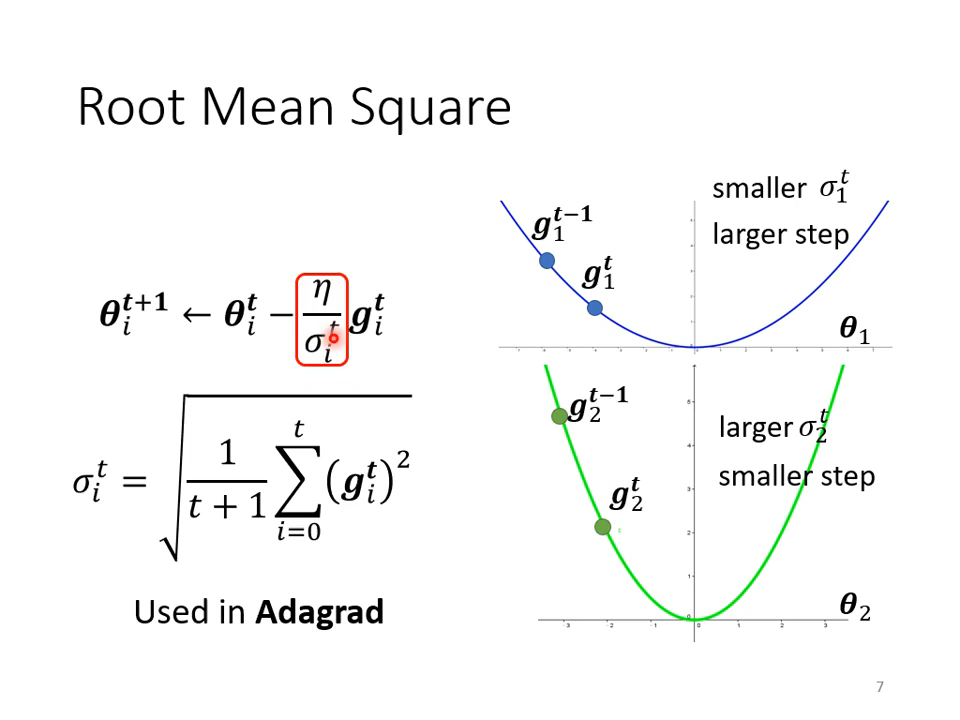
使用平方根来结合以前梯度
但这并不完美,所以需要继续改进
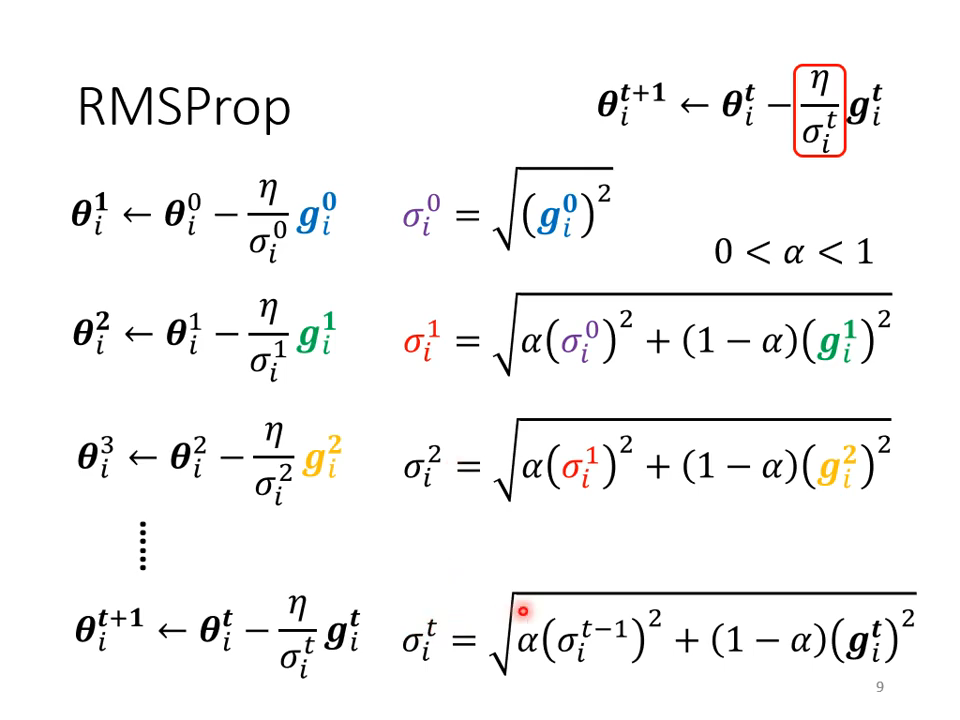
吐槽一下,这不是低通滤波吗?确实具备自适应能力
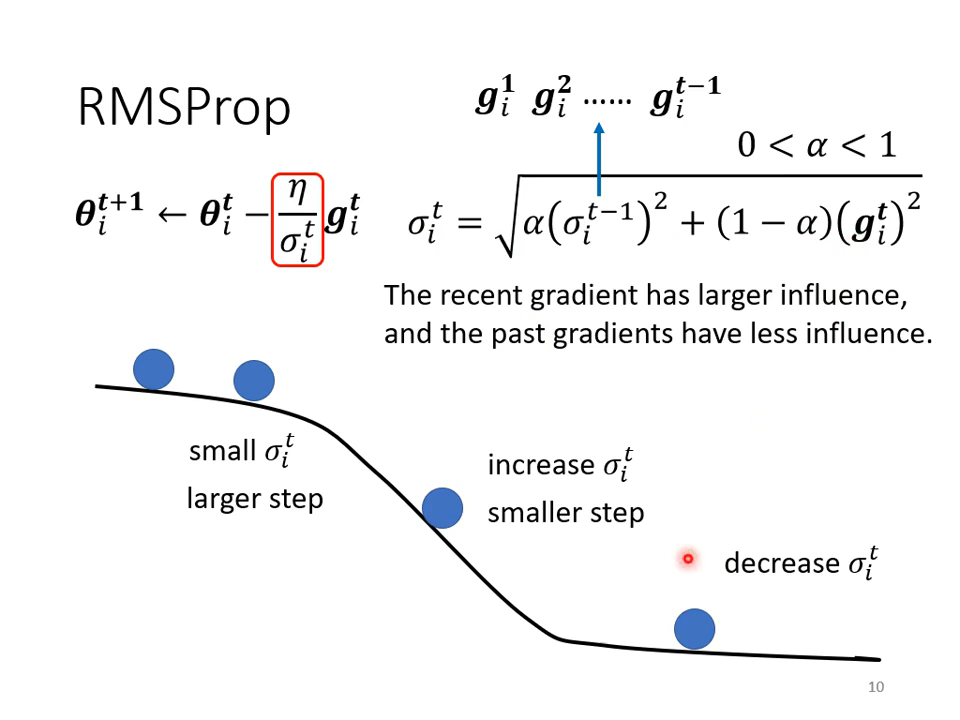
举例说明

!!!好多深度学习框架里都见过这个方法!
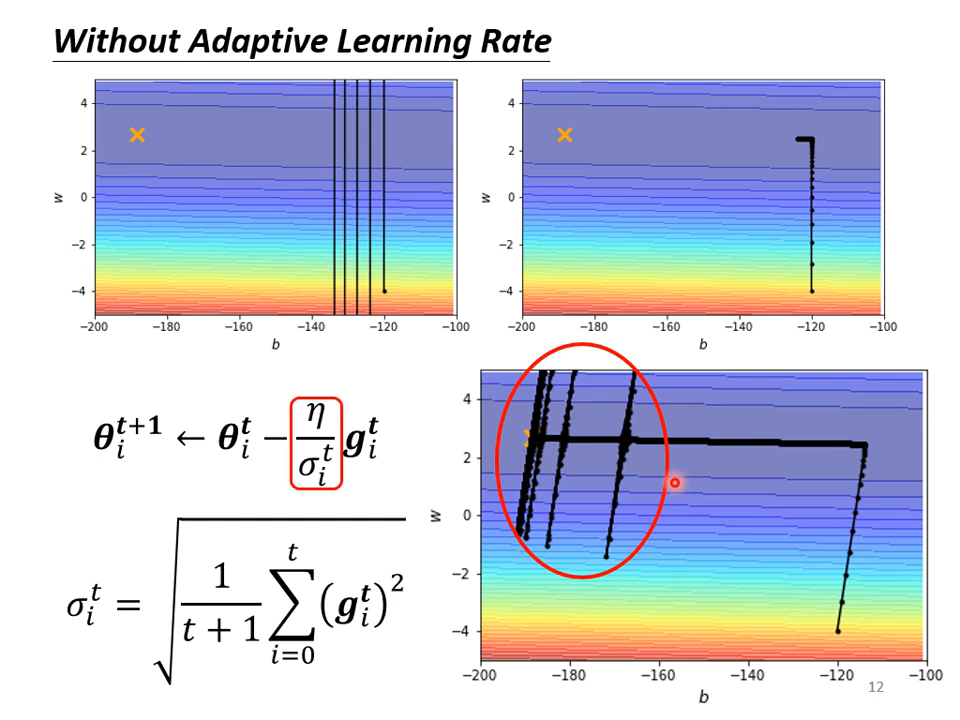
为什么会喷射?
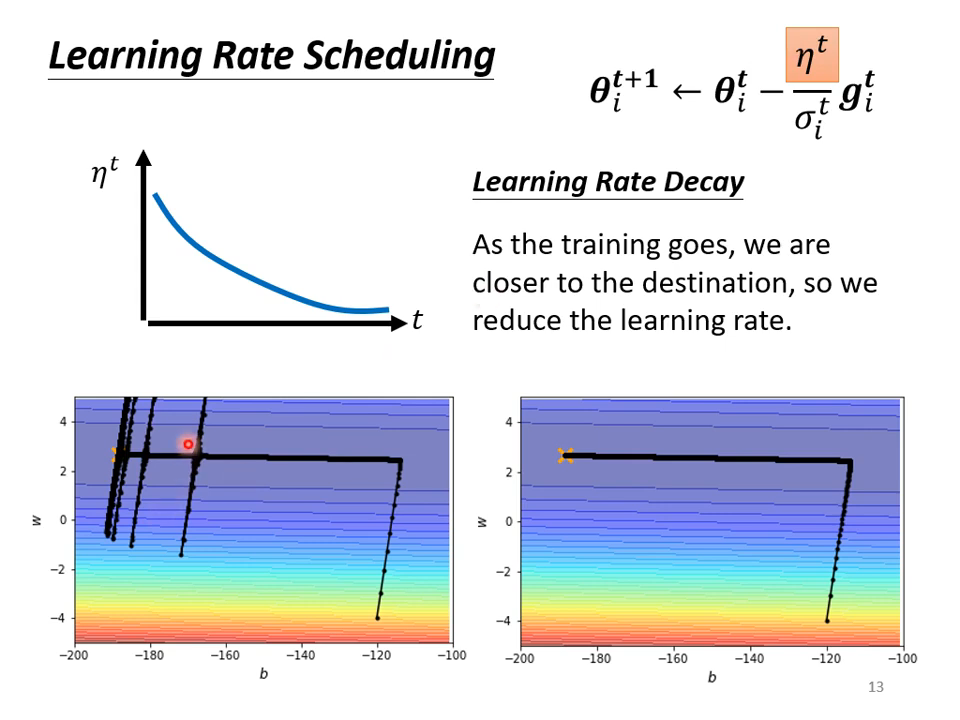
再增加一个超参数!
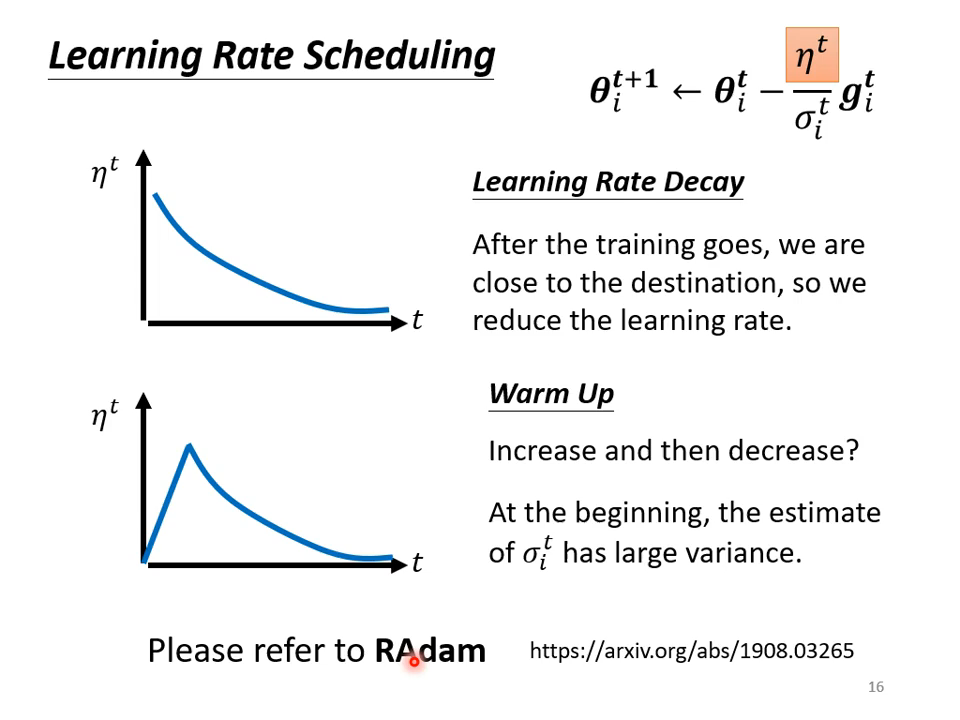
warmup策略!还有上面提到的learning rate decay,都是经常用到的技巧。
总结一下最终版本的梯度下降: