[人工智能]Pytorch实验一：从零实现Logistic回归和Softmax回归

作者：北京交通大学计算机学院 秦梓鑫
学号：21120390
写这篇文章的原因，是因为实验报告中不能大量粘贴代码。但很多坑的点不保存下来又很可惜，于是决定发到CSDN上。
内容仅供学习参考，如有错误之处请大家多多指正。版权所有，转载请注明出处。请勿用于任何形式的课程作业。

实验原理

PyTorch基本操作实验

实验内容是创建张量、计算张量的转置和乘积以及跟踪张量的梯度属性在计算中的变化；此实验的主要目的是熟悉PyTorch框架中和Tensor相关的基本操作，并验证PyTorch的自动求导机制的正确性。

Logistic 回归实验

实验内容包括用两种方式实现Logistic回归算法：手动实现和借助torch.nn模块实现。算法实现后，需构造数据集对算法进行测试，以loss和accuracy为指标对结果进行分析。实验的目的是了解Logistic回归算法的原理和实现过程。

Logistic回归算法是一种用于处理二分类问题的线性模型，它的特点是：使用Logistic函数作为线性模型的激活函数，以解决连续的线性函数不适合进行分类的问题[1]。在Logistic回归中，对输入向量$\text{x}\in {\mathbb{R}}^D$，输出是标签y=1时的后验概率，定义为：
$$p\left(y=1|\text{x}\right)=\sigma \left({\mathbf{w}}^t\mathbf{x}\right)=\frac{1}{1+exp\left(?{\text{w}}^t\text{x}\right)}\in (0,1)$$
值得注意的是：${\text{w}}^t\text{x}$已经包含了偏置项$b$，这里略去。特别地，对于二分类问题，对标签y=0时的概率估计也可以计算：
$$p\left(y=0|\text{x}\right)=\sigma \left({\text{w}}^t\text{x}\right)=\frac{exp\left(?{\text{w}}^t\text{x}\right)}{1+exp\left(?{\text{w}}^t\text{x}\right)}\in (0,1)$$
训练时，Logistic回归使用交叉熵作为损失函数，对参数进行更新。
$$R(\text{w})=\sum _i^n?ylog\left(\hat{y}\right)?\left(1?y\right)log\left(1?\hat{y}\right)$$
其中， y ∈ { 0 , 1 } y\in\{0,1\} y∈{0,1}是训练集样本的真实标签，$\hat{y}$是由(1)和(2)计算的后验概率。
对单个样本计算出损失后，可使用梯度下降法或牛顿法进行优化求解。

Softmax回归实验

和Logistic回归相似，Softmax回归也是线性模型的一种。它用于求解多分类问题：给定样本$\text{x}\in {\mathbb{R}}^D$，寻找其与样本标签 y ∈ { 1 , 2 , … , C } y\in\{1,2,\ldots,C\} y∈{1,2,…,C}的映射。
首先，我们介绍Softmax函数。其定义如下：给定长度为K的向量$\text{s}=\left[x_1,x_2,..,x_K\right]$，对其中的元素$x_k$，有
$$y_k=softmax\left(x_k\right)=\frac{exp\left(x_k\right)}{{\sum }_{i=1}^{K}exp\left(x_i\right)}$$

函数的特性是：将序列$\text{s}$映射为一个新的序列$\text{y}=\left[y1,y2,\dots ,y_K\right]$，满足：
$$?k,y_k\in \left(0,1\right),\sum _{k=1}^K{y}_k=1$$

在Torch中，可以通过loss=nn.LogSoftmax()函数直接计算Softmax值；由于定义中含有指数运算，可能会造成浮点误差，需要对数据进行预处理。
对于多分类问题，Softmax回归预测样本$\text{x}$属于类别$c$的条件概率为：
$$p\left(y=c|\text{x}\right\}=softmax\left({\text{w}}_c^t\text{x}\right)=\frac{exp\left({\text{w}}_c^t\text{x}\right)}{{\sum }_{c^{\prime }=1}^{C}exp\left({\text{w}}_{c^{\prime }}^t\text{x}\right)}$$
为得到输出类别，需定义决策函数（计算loss时无用；输出accuracy时有用）：
$$\hat{y}={arg}_{c=1}^{C}maxp\left(y=c|x\right)$$
训练时，Softmax回归采用针对多个类别的交叉熵函数作为损失，进行优化：
$$R\left(\text{w}\right)=\sum _i^n\sum _c^C?ylog\left(\hat{y}\right)?\left(1?y\right)log\left(1?\hat{y}\right)$$
其中， y ^ ∈ { 0 , 1 } \hat{y}\in\{0,1\} y^?∈{0,1}是训练集样本中：判断样本$\text{x}$是否属于$c$类的真实标签，$y$是由(7)计算出的条件概率。损失函数计算出后，可通过反向传播算法计算损失函数对于参数$\text{w}$的偏导数，从而利用梯度下降法进行优化。

实验环境和数据集

• 本实验在笔记本电脑上开展。笔记本的处理器型号为：Intel? Core? i7-10510U CPU @ 1.80GHz
  2.30 GHz；RAM大小为16GB；系统环境为Windows 64位。程序运行环境是：Anaconda Shell, Python 3.8.10。
• 人工构造的二分类数据集包括100个二维空间内的点作为样本，分为两类。
• Fashion-MNIST是一个十分类的数据集，每个样本为一张28281的图片。其中，训练集60000张，测试集约10000张。

实验过程和代码

PyTorch基本操作实验

张量减法的实现

m = torch.tensor([1,2,3])
print('m=',m)
n = torch.tensor([[-1],[-1]])
print(m-n)
print(torch.sub(m,n))
print(m.sub(n))

从代码块我们可以看到，PyTorch中实现运算主要有三种方式：直接用运算符、使用torch模块中定义的sub函数、使用张量类中定义的运算方法（很重要，而不是把张量送到Math库中运算，会导致张量计算图无法传递）。三种方式运算时，m和n本身的值没有发生改变；但计算过程中，由于m和n属于不同的维度，且数据范围分别是1×3和2×1，是可广播的(broadcastable)。

可广播的判断方法是：从两个运算张量的数据维度的最后一项往前看，两者要么相等，要么是一。

因此，根据广播机制，m被扩充为了$[[1,2,3],[1,2,3]]$；n被扩充为了$[[?1,?1,?1],[?1,?1,?1]]$。在此之后，两个扩充的向量进行了减法运算。

张量乘法的实现

p = torch.normal(mean=0,std=0.01,size=(3,2))
print('p=',p)

q = torch.normal(mean=0,std=0.01,size=(4,2))
print('q=',q)

q_trans=torch.transpose(q,0,1)
print('q_trans=',q_trans)

product = torch.mm(p,q_trans)
print(product)

生成正态分布的矩阵，并计算矩阵P和Q乘积的代码如上。

张量梯度的跟踪

首先，我们创建一个1×1的张量。注意requires_grad属性默认为False，需要手动设置为True。之后，我们依次计算：
$y1=x2,y2=x3,y3=y1+y2.$ 并调用反向传播函数计算$\frac{dy1}{dx},\frac{dy2}{dx},\frac{dy3}{dx}$的值。

这个过程中需要注意的是：

• 只有计算图中的叶子节点，才可以访问grad属性。
• 每次调用反向传播方法后，需要手动设置retain_graph=True以保留之前的计算图；否则之前的计算图会废弃。
• 每次计算出梯度后，要使用grad.zero_()方法清零梯度。否则每次计算得到的梯度会累加。在网络中，先用optimizer.zero()清零梯度，用loss.backward()回传梯度，最后通过optimizer.step()更新参数。

计算过程的代码如下：

x = torch.tensor(1.0,requires_grad=True)
y1 = torch.pow(x,2)
y1.backward(retain_graph=True)
print("dy1/dx:",x.grad)
x.grad.zero_()

y2 = torch.pow(x,3)
y2.backward(retain_graph=True)
print("dy2/dx:",x.grad)
x.grad.zero_()

y3 = y1 + y2
y3.backward(retain_graph=True)
print("dy3/dx:",x.grad)
x.grad.zero_()

Logistic 回归实验

从0实现 logistic 回归 (除了反向传播和交叉熵)

（1）数据集预处理和读取
数据集读取是通过迭代器(iterator)实现的。迭代器生成函数获取批量大小、输入的特征和标签，对标签的序号(index)进行随机打乱；每次在调用时，返回一批(batch)数据的特征向量矩阵和对应标签的列向量。

# feeding whole data set
# return vector instance: batchsize * 2 (represent x and y) and label (batchsize * 1)
def data_iter(batch_size, features, labels):
    num_examples = len(features)
    indices = list(range(num_examples))
    random.shuffle(indices) # 样本的读取顺序是随机的
    for i in range(0, num_examples, batch_size):
        j = torch.LongTensor(indices[i: min(i + batch_size, num_examples)]) # 最后一次可能不足一个batch
        yield features.index_select(0, j), labels.index_select(0, j)

（2）参数初始化
由于本数据集样本较少，线性模型的权重采用非标准的正态分布，增加数据的离散程度。

# parameter initialization
w = torch.tensor(np.random.normal(1,3,(2,1)),dtype=torch.float32)
w_init = w # the initial weights
b = torch.zeros(1,dtype=torch.float32)
w_init = b # initial bias
w.requires_grad_(requires_grad=True)
b.requires_grad_(requires_grad=True)

（3）定义模型、损失、优化
李宏毅老师在深度学习课上讲过：

把大象装进冰箱只需要三步。
First, define the model.
Then, define the loss.
Gradient Desent (inc optimizer, accuracy tester and iteration process) ~

模型
线性模型，激活函数为softmax函数：

def lin_reg(X,w,b):
    return torch.mm(X,w)+b
def softmax(X):
    X_exp = torch.exp(X)
    partition = X_exp + torch.ones(X.size())
    predict = 1 / partition
    return predict # 这里应用了广播机制

损失函数
对于每个batch的预测结果和真实标签，其二元交叉熵损失定义如下：

import math # never do this!
def entropy_loss(yhat, y):
    loss =  nn.BCELoss()
    total = loss(yhat.squeeze(), y)
    return torch.sum(total)/y.shape[0]

这里采用的是torch自带的 Binary Cross Entropy Loss。Torch中自带的计算函数具有更好的数值准确度。稍后我们会手动实现交叉熵函数。值得注意的是yhat是维度为$10\times 1$的张量，而y的维度是$10$，两者不能直接计算。所以需要调squeeze函数对yhat进行挤压操作。
优化器、检验器和优化过程
采用随机梯度下降算法进行优化。优化方法如下：

# optimization
lr = 0.01
num_epochs = 10
batch_size = 2

def sgd(params, lr, batch_size):
    for param in params:
        param.data -= lr * param.grad / batch_size 

检验部分写在前面的目的是，希望能在训练时实时输出Accuracy. 测试指标(metric)包括：在训练集上的accuracy和loss. 注意yhat是大小为10×1的张量，而y是大小为10的张量。不能直接比较运算。因此需要调用squeeze()方法进行归一化。

def evaluate_accuracy(batch_size,features,label):
    acc_sum, n = 0.0, 0
    for X, y in data_iter(batch_size,features,label):
        yhat = torch.round(softmax(lin_reg(X, w, b)))
        d = ( yhat.squeeze() == y).float().sum().item()
        acc_sum +=d
        n += y.shape[0]
    return acc_sum / n

训练过程

for epoch in range(num_epochs):
    for instance,label in data_iter(batch_size,x,y):
        predict = softmax(lin_reg(instance, w, b))
        l =  entropy_loss(predict,label)
        l.backward()
        sgd([w,b],lr,batch_size)
        w.grad.data.zero_()
        b.grad.data.zero_()
    #print(w)
    epoch_loss =  entropy_loss(softmax(lin_reg(instance,w,b)),label)
    print('epoch %d,loss %f' % (epoch+1,epoch_loss.mean().item()))
    epoch_acc = evaluate_accuracy(batch_size,x,y)
    print('acc %f' % epoch_acc)

用 torch.nn 实现 logistic 回归

（1）数据的读取和预处理
使用torch中的Data.TensorDataset定义数据集较为简便：

# Logistic Regression from Torch.nn
import torch.utils.data as Data
batch_size = 10
# from previous data generation
features, labels = x,y
dataset = Data.TensorDataset(features, labels)
# put dataset into DataLoader
data_iter = Data.DataLoader(dataset=dataset,batch_size=batch_size, shuffle=True, num_workers=0,)

（2）定义模型、损失、优化方法
模型
__init__中定义网络；forward中定义计算图

class LogisticNet(nn.Module):
    def __init__(self,d1,d2):
        super(self).__init__()
        self.linear = nn.Linear(d1,d2)
        self.sigmoid = nn.Sigmoid()

    def forward(self, x):
        y = self.linear(x)
        z = self.sigmoid(y)
        return z

net = LogisticNet(2,10)

损失
一行代码完成交叉熵损失。

loss = nn.CrossEntropyLoss()

优化
优化器：采用随机梯度下降

import torch.optim as optim
optimizer = optim.SGD(net.parameters(), lr=0.01)

（3）定义检验方法和优化过程
检验器：注意，这里需要使用arg max决策函数来输出label了（因为标签不是one-hot的形式）。

def evaluate_accuracy(data_iter, net):
    acc_sum, n = 0.0, 0
    for X, y in data_iter:
        acc_sum += (net(X).argmax(dim=1) == y).float().sum().item()
        n += y.shape[0]
    return acc_sum / n

优化过程

num_epochs = 30

for epoch in range(1, num_epochs + 1):
    for X, y in data_iter:
        output = net(X)
        l = loss(output, y.flatten().long())
        optimizer.zero_grad()  # 梯度清零，等价于net.zero_grad()
        l.backward()
        optimizer.step()
    acc = evaluate_accuracy(data_iter,net)
    print('epoch %d, loss: %f, acc: %f' % (epoch, l.item(),acc))

Softmax 回归实验

从0实现 softmax 回归 (除了反向传播)

（1）读取数据

import torch
import torchvision
import torchvision.transforms as transforms

mnist_train = torchvision.datasets.FashionMNIST(root='~/Datasets/FashionMNIST', train=True,
download=True, transform=transforms.ToTensor())
mnist_test = torchvision.datasets.FashionMNIST(root='~/Datasets/FashionMNIST', train=False,
download=True, transform=transforms.ToTensor())


num_workers = 0
train_iter = torch.utils.data.DataLoader(mnist_train, batch_size=batch_size, shuffle=True,
                                         num_workers=num_workers,drop_last= True)
test_iter = torch.utils.data.DataLoader(mnist_test, batch_size=batch_size, shuffle=False,
                                        num_workers=num_workers,drop_last=True)

（2）参数初始化

w = torch.tensor(np.random.normal(1,1,(784,10)),dtype=torch.float32)
b = torch.zeros(1,dtype=torch.float32)
w.requires_grad_(requires_grad=True)
b.requires_grad_(requires_grad=True)

（3）定义模型、损失和优化
模型 线性模型，因为直接计算softmax会产生浮点误差，所以没有在这里加激活函数。

def lin_reg(X,w,b):
    xsize = X.size()
    return torch.mm(X.reshape(-1,784),w)+b

损失 多元交叉熵损失，注意这里为了避免溢出，手动实现Softmax函数时有一个trick。

# loss
import numpy as np

def softmax(X):
    # 计算每行的最大值
    row_max = X.max(axis=1).values
    # 每行元素都需要减去对应的最大值，否则求exp(x)会溢出，导致inf情况；这个trick不影响softmax的结果
    row_max = row_max.reshape(-1, 1)
    X = X - row_max
    X_exp = torch.exp(X)
    partition = X_exp + torch.ones(X.size())
    predict = X_exp / partition
    return predict #这里应用了广播机制

def entropy_loss(yhat, y):
    loss = 0.0
    for i in range(0,batch_size):
        #print(y)
        y_softmax = softmax(yhat)
        index = y[i]
        loss -= y_softmax[i][index].log() #不能用Math.log
        #print(loss)
    return loss

优化

• 优化器

def sgd(params, lr, batch_size):
    for param in params:
        param.data -= lr * param.grad / batch_size # 注意这里更改param时用的param.data

• 检验器

def evaluate_accuracy(iter):
    acc_sum, n = 0.0, 0
    for X, y in iter:
        torch.reshape(X,(-1,784))
        y_out = softmax(lin_reg(X, w, b))
        value,index = y_out.max(axis=1)
        yhat = torch.tensor(index,dtype=int)
        d = ( yhat== y).sum().item()
        acc_sum +=d
        n += y.shape[0]
    return acc_sum / n

• 优化过程

# Hyperparameters
lr = 0.01
num_epochs = 20
batch_size = 256

for epoch in range(num_epochs):
    train_size = 0
    for data in train_iter:
        train_size +=1
        instance, label = data[0],data[1]
        predict = lin_reg(instance, w, b)
        l =  entropy_loss(predict,label)
        l.backward()
        sgd([w,b],lr,batch_size)
        w.grad.data.zero_()
        b.grad.data.zero_()
    print(train_size)

    #test accuracy
    epoch_loss = 0
    test_size = 0
    for data in test_iter:
        instance, label = data[0], data[1]
        epoch_loss +=  entropy_loss(lin_reg(instance,w,b),label)
        test_size += 1
    print(test_size)
    print('epoch %d,loss %f' % (epoch+1,(epoch_loss.item())/ test_size))
    epoch_acc = evaluate_accuracy(test_iter)
    epoch_acc2 = evaluate_accuracy(train_iter)
    print('acc %f on test set, %f on training set' % (epoch_acc,epoch_acc2))

利用torch.nn实现 softmax 回归

（1）定义超参数、读取数据

# Hyperparameters
lr = 0.01
batch_size = 3
num_workers = 0


# data
import torch
import torchvision
import torchvision.transforms as transforms

mnist_train = torchvision.datasets.FashionMNIST(root='~/Datasets/FashionMNIST', train=True,
download=True, transform=transforms.ToTensor())
mnist_test = torchvision.datasets.FashionMNIST(root='~/Datasets/FashionMNIST', train=False,
download=True, transform=transforms.ToTensor())

train_iter = torch.utils.data.DataLoader(mnist_train, batch_size=batch_size, shuffle=True,
                                         num_workers=num_workers,drop_last= True)
test_iter = torch.utils.data.DataLoader(mnist_test, batch_size=batch_size, shuffle=False,
                                        num_workers=num_workers,drop_last=True)

（2）定义模型、损失和优化方法

# Model
import torch
import torch.nn as nn

class SoftmaxReg(nn.Module):
    def __init__(self,n_feature):
        super().__init__()
        # define the transform dimensions
        self.linear = nn.Linear(n_feature,10)
    def forward(self,x):
        y = self.linear(x)
        return y

feature_length = 784

net = SoftmaxReg(feature_length)

# Loss
loss = torch.nn.NLLLoss()

#optimization
import torch.optim as optim
optimizer = optim.SGD(net.parameters(), lr=0.03)

（3）定义测试和优化过程

def evaluate_accuracy(iter):
    acc_sum, n = 0.0, 0
    for X, y in iter:
        X = torch.reshape(X, (-1,feature_length))
        m = nn.LogSoftmax(dim=1)
        y_out = m(net(X))
        value, index = y_out.max(axis=1)
        yhat = torch.tensor(index, dtype=int)
        d = (yhat == y).sum().item()
        acc_sum += d
        n += y.shape[0]
    return acc_sum / n


num_of_epochs = 20
for epoch in range (0, num_of_epochs):
    for instance, label in train_iter:
        normal_instance = torch.reshape(instance,(batch_size,-1))
        output = net(normal_instance)
        criteria = nn.NLLLoss() #调用loss函数必须分开定义；NLLloss可以直接映射到非onehot vector
        m = nn.LogSoftmax(dim=1) #使用Torch自带的Softmax函数，精度更高
        l = criteria(m(output),label)
        l.backward()
        optimizer.step()
        optimizer.zero_grad()
        #print('epoch %d, loss: %f' % (epoch, l.item()))
    epoch_loss = 0
    test_size = 0
    for data in test_iter:
        instance, label = data[0], data[1]
        criteria = nn.NLLLoss()
        m = nn.LogSoftmax(dim=1)
        epoch_loss += criteria(m(net(instance.reshape(-1,784))), label)
        test_size += 1
    print('epoch %d,loss %f' % (epoch+1,(epoch_loss.item())/ test_size))
    epoch_acc = evaluate_accuracy(test_iter)
    epoch_acc2 = evaluate_accuracy(train_iter)
    print('acc %f on test set, %f on training set' % (epoch_acc,epoch_acc2))

实验结果

PyTorch基本操作实验

1.张量减法的实现

结果如上，可以验证：三种方式都可以实现张量减法，且都触发了PyTorch中的广播机制。实验结果与之前的计算结果一致。
2.张量乘法的实现
运行结果如下：

可以看到，向量$\text{P}$和${\text{Q}}^{\text{t}}$分别属于3×2和2×4的矩阵，可以进行乘法运算。
3.张量梯度的跟踪
根据公式(10)、(11)和(12)，可以验证：$\frac{dy1}{dx}=2x=2,\frac{dy2}{dx}=3x^2=3,\frac{dy3}{dx}=3x^2+2x=5.$
实验结果如下：

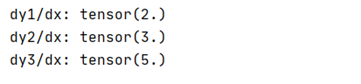
可知，计算结果和理论推导一致。

Logistic回归实验

手动实现：由于数据集样本数较小，超参数的影响变化不明显。多次调试参数后，结果显示：学习率为0.01，num_epochs 设置为 10，batch_size 设置为 2时，可以在 测试集上观察到loss的下降和accuracy的上升。

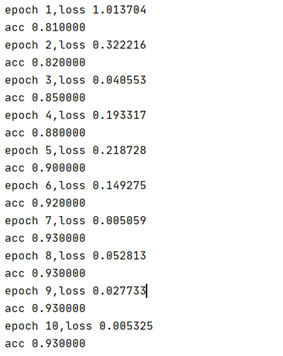
torch实现：结果显示：学习率为0.01，num_epochs 设置为 10，batch_size 设置为 10时，可观察到loss下降和accuracy上升。

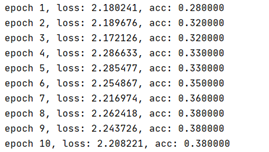
Softmax回归实验

手动实现：学习率为0.01，num_epochs 设置为 5，batch_size 设置为 10时，可观察到loss下降，在训练集和测试集的accuracy呈上升趋势。

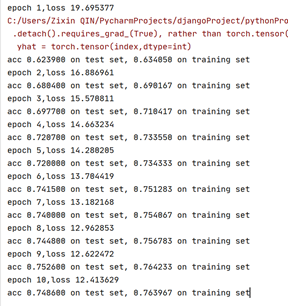
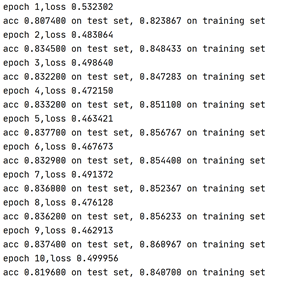
torch实现：学习率为0.01，num_epochs 设置为 10，batch_size 设置为 10时，可观察到loss下降，在训练集和测试集的accuracy呈上升趋势。

参考文献

[1] 邱锡鹏，神经网络与深度学习，机械工业出版社，https://nndl.github.io/, 2020.