论文解读之:
Towards Accurate One-Stage Object Detection with AP-Loss
这篇论文是关于one-stage目标检测的一篇论文,作者通过提出一种AP损失,直接对评价指标构成的损失函数进行训练。

写在前面
在目标检测领域,有着两种主要的思路:One-stage与Two-stage。其中,one-stage的目标检测是同时进行目标的定位与识别,而two-stage是分为两步,首先生成一系列候选框,然后对其进行识别分类。one-stage方法包括YOLO、SSD等常见网络,而two-stage方法包括Faster RCNN等常见网络。
两种目标检测的思路各有利弊,one-stage的方法效率高,但是准确率不如two-stage。这篇文章的作者研究了one-stage的问题。在one-stage目标检测中,一个重要的问题就是锚点数量过大,导致了前背景极度不平衡。
在目标检测中,常用的评价指标包括mean AP、IoU等。其中AP是不可微的,且是非凸的,所以如果使用传统的梯度下降方法无法进行优化。所以之前的方法都是构造其他损失函数,而我们能不能把AP构造成能学习的损失函数呢?如果可以的话,从评价指标的角度看这样的学习更直接。
另外,还有一个很尴尬的情况,就是由于正负样本不均衡的原因,导致检测的结果很垃圾但是分类准确率依然很高,如下图所示:
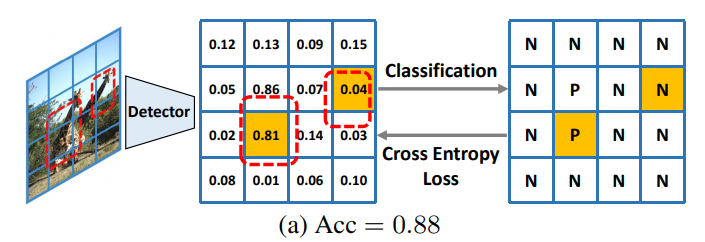
本文的作者提出了一种使用AP loss的学习方法,根据论文中的说法,本篇论文的贡献如下:
贡献
- 提出了一种新的one-stage目标检测框架,该框架采用排序损失来处理不平衡问题。
- 提出了一种误差驱动学习算法,通过理论和实验验证,该算法能够有效地优化不可微且非凸的基于AP的损失函数。
- 在不改变模型结构的情况下,对于不同类型的分类损失,文章提出的方法性能能达到先进水平。
作者主要提出了AP损失,并创造了学习这种不可微损失的学习方法。其中AP损失是通过将分类问题替换为排序问题设计出来的。所以理解本文主要分为两个部分:损失函数设计与训练方法。
AP损失函数
首先,在传统检测器特征提取后,每个anchor box将产生K+1维的得分,分别对应K个类别和背景。为了便于后面排序,作者将每个anchor box复制K个,每个anchor box在特征提取阶段仅得到一个得分,用于代表对应的某一个类的得分。
设
B
B
B为anchor box集合,
b
i
b_i
bi?为第
i
i
i个anchor box。在检测器提取特征后,每一个anchor box得到一个得分
s
i
s_i
si?和一个二进制标签
t
i
t_i
ti?,这个标签指示这个anchor box是前景还是背景,前景取1,背景取0。
然后计算差分,将
s
i
s_i
si?转为
x
i
j
x_{ij}
xij?,其中
θ
\theta
θ为特征提取过程中CNN的参数。
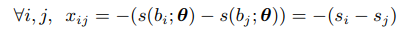
这个
x
i
j
x_{ij}
xij?就指示了
s
i
s_i
si?的排序,如果
x
i
j
>
0
x_{ij}>0
xij?>0说明
s
i
s_i
si?排在
s
j
s_j
sj?后面。所以可以想到,统计对于同一个
i
i
i时,所有
j
j
j里
x
i
j
>
0
x_{ij}>0
xij?>0的个数,就得到了
s
i
s_i
si?的排序。
接着,作者将
t
i
t_i
ti?转化为了
y
i
j
y_{ij}
yij?:
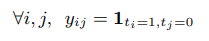
即只有当
i
i
i为前景,
j
j
j为背景时,
y
i
j
y_{ij}
yij?取1。
接着就能得到当前排序在总体中的占比,其中分母上加一表示加上
k
=
i
k=i
k=i的那一个:
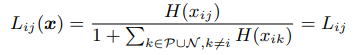
其中
H
(
.
)
H(.)
H(.)为阶跃函数:
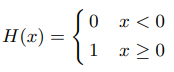
P
\mathcal P
P表示前景anchor box,即正样本,
N
\mathcal N
N表示背景anchor box,即负样本。
最终AP损失可以表示为:
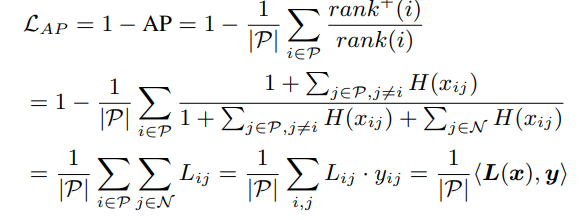
其中
r
a
n
k
(
i
)
rank(i)
rank(i)为第
i
i
i个anchor box在所有anchor box中的排序,
r
a
n
k
+
(
i
)
rank^+(i)
rank+(i)表示第
i
i
i个anchor box在正样本中的排序。在正样本中的排序肯定小于总的排序,当所有正样本都排在负样本前面时,这个分式值为1,即是最大值,所以这样设计是合理的,最终的
L
A
P
L_{AP}
LAP?越小越好,所以优化目标可以写为:
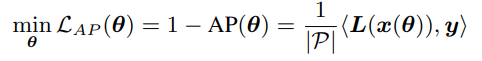
由于函数
L
(
.
)
L(.)
L(.)是不可微的,所以不能用梯度下降来学习,需要新的学习策略,这就是作者在下文中提出的学习策略。
优化算法
作者的方法结构如下图所示:
其中Difference Transformation就是上述
s
i
、
s
j
s_i、s_j
si?、sj?到
x
i
j
x_{ij}
xij?的转换,Activation Function就是上述
L
i
j
(
x
)
L_{ij}(x)
Lij?(x),Ranking Label Transformation就是上述
t
i
、
t
j
t_i、t_j
ti?、tj?到
y
i
j
y_{ij}
yij?的转换。
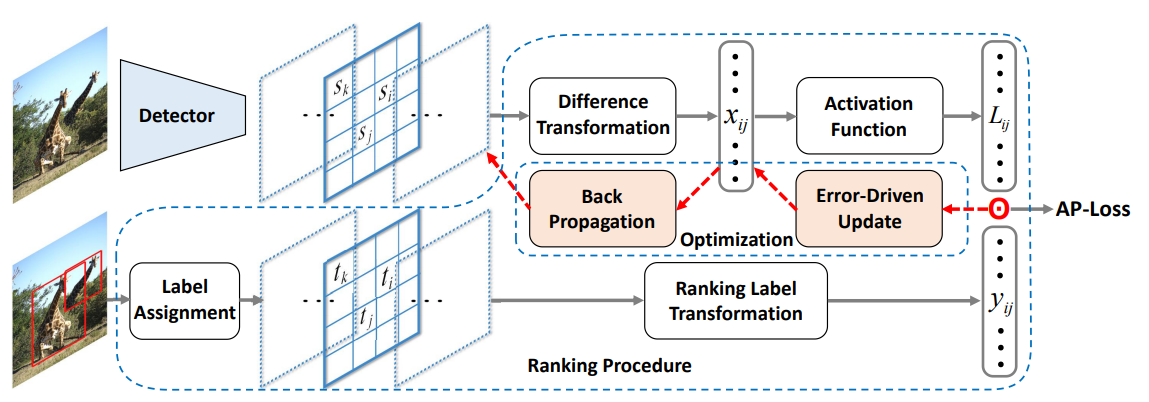
由整个流程可以看出,目前损失函数AP loss由前面得出的
L
i
j
L_{ij}
Lij?产生,在反向传播的时候不可导的部分就是Activation Function。所以在这个位置设计优化算法,得到
x
i
j
x_{ij}
xij?的更新值
Δ
x
i
j
\Delta x_{ij}
Δxij?,然后由这个值往前的部分用梯度下降反向传播即可。所以问题就在于求
x
i
j
x_{ij}
xij?的更新值
Δ
x
i
j
\Delta x_{ij}
Δxij?。
设
L
i
j
L_{ij}
Lij?的期望值为
L
i
j
?
L_{ij}^*
Lij??,定义近似的更新规则:
Δ
x
i
j
=
L
i
j
?
?
L
i
j
\Delta x_{ij}=L_{ij}^*-L_{ij}
Δxij?=Lij???Lij?
又由于当
L
i
j
?
y
i
j
=
0
L_{ij}*y_{ij}=0
Lij??yij?=0的时候,AP loss达到最小值。所以当
y
i
j
y_{ij}
yij?取1时,我们使
L
i
j
L_{ij}
Lij?的期望值为0。当
y
i
j
y_{ij}
yij?取0时,我们不需要进行更新,这时
L
i
j
L_{ij}
Lij?的期望值默认设为0,上式便可以简化为:
Δ
x
i
j
=
?
L
i
j
?
y
i
j
\Delta x_{ij}=-L_{ij}*y_{ij}
Δxij?=?Lij??yij?
我们得到了
x
i
j
x_{ij}
xij?的更新方式,接下来就是得出网络权重的更新方式。我们可以将问题写成以下的优化问题,使用点积来衡量两个向量的相似度,使得更新
θ
\theta
θ前后
x
x
x的变化趋近于上面得到的
Δ
x
\Delta x
Δx。最后再加一个L2正则项。
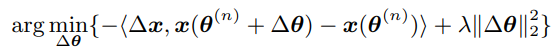
解决这个优化问题即可得到
Δ
θ
\Delta \theta
Δθ。将
x
(
θ
)
x(\theta)
x(θ)在
θ
(
n
)
\theta^{(n)}
θ(n)处一阶展开,得到下式:
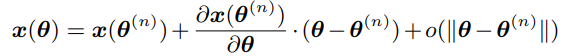
忽略高阶无穷小,将上式带入优化问题,可以得到:
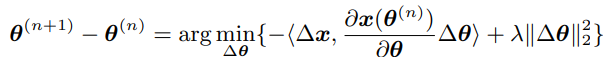
这就是
θ
\theta
θ的更新策略。
如前面所说,这部分是可导的,所以这些推导可以忽略,直接将
x
i
j
x_{ij}
xij?的梯度设置为
Δ
x
i
j
\Delta x_{ij}
Δxij?,之后用反向传播即可。
训练细节
1、minibatch
minibatch 训练准则在深度学习框架中应用广泛,比使用单个样本训练的过程更为稳定。且有助于优化方法规避 “score-shift” 情况。
AP-loss 可以从一个 batch 中获得,也可以从具有多个 anchor 的单个图像中获得。
mini-batch 训练是保证好的收敛性和准确性的重要前提。
2、分段阶跃函数
训练初期,得分
s
i
s_i
si?之间非常接近(即几乎所有的
H
(
x
)
H(x)
H(x)输入都接近于0),所以,输入的一个微小的改变将会带来一个大的输出改变。为了避免这个问题,将原来的阶跃函数代替为如下函数:
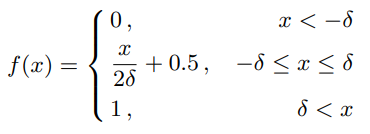
总结
这篇论文一转之前的目标识别思路,直接将评价指标作为优化目标,得到了很好的效果。在这个过程中,作者设计了AP loss,由于AP的不可导,作者又设计了专用的学习方法。同时,这个AP loss具有很好的性质,解决了样本不均衡问题。所以这个文章的方法很创新,并且效果很好。