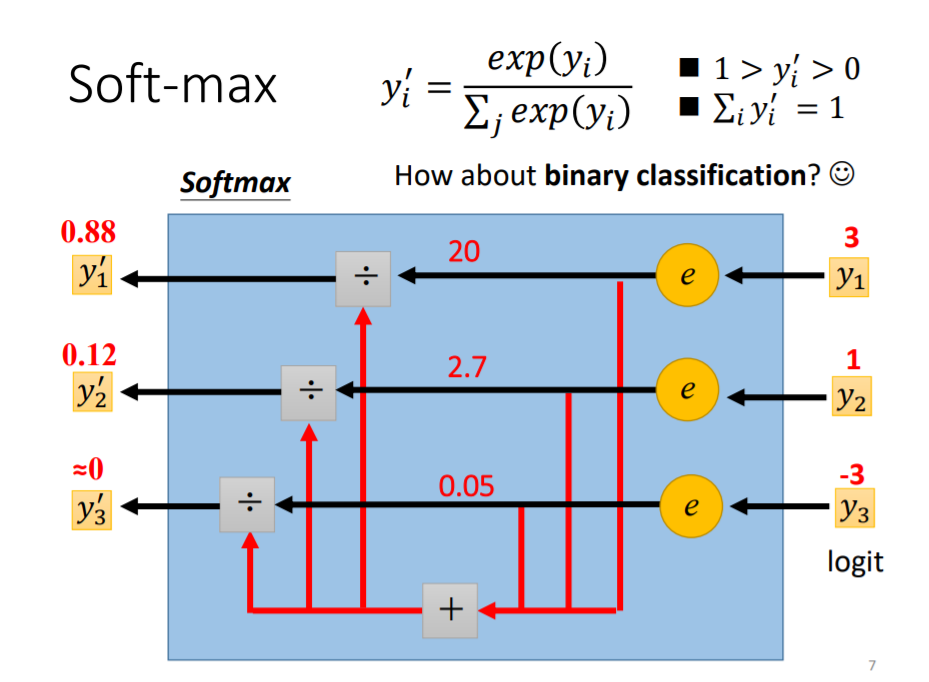
1. 局部最小值与鞍点
1.1 相关定义:
- critical point:梯度(gradient)为零的点
- local minima(局部最小值)
- saddle point(鞍点):一个不是局部最小值的驻点(一阶导数为0的点)
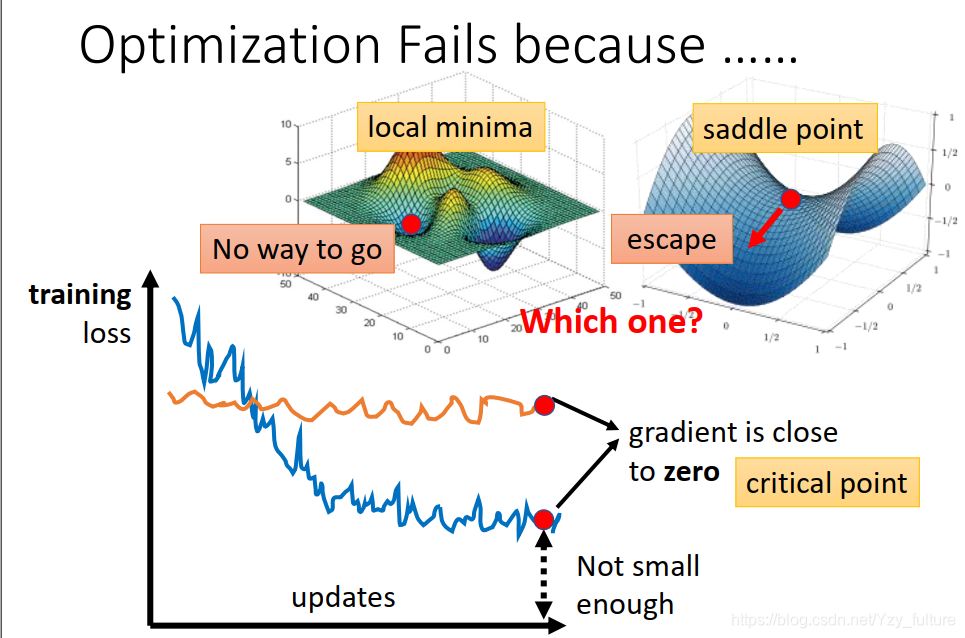
1.2 梯队逼近为0的原因
可能是因为卡在了critical point上。但我们知道,这里面有两种情况
- 卡在了local minima。此时没有路可以走
- 卡在了saddle point。此时还有路可以走,可以是loss更低
所以,我们需要对critical point的情况进行分析
情况的判断
- 将loss函数通过泰勒展开式写成以下形式:

- 判断:此时可以通过在
θ
′
\theta^{'}
θ′处error surface的形式的分析,可以判断出此时的
θ
′
\theta^{'}
θ′是处于local minima还是saddle point
如果走到了一个critical point,意味着gradient为0,即绿色的一项为0,只剩下红色的一项
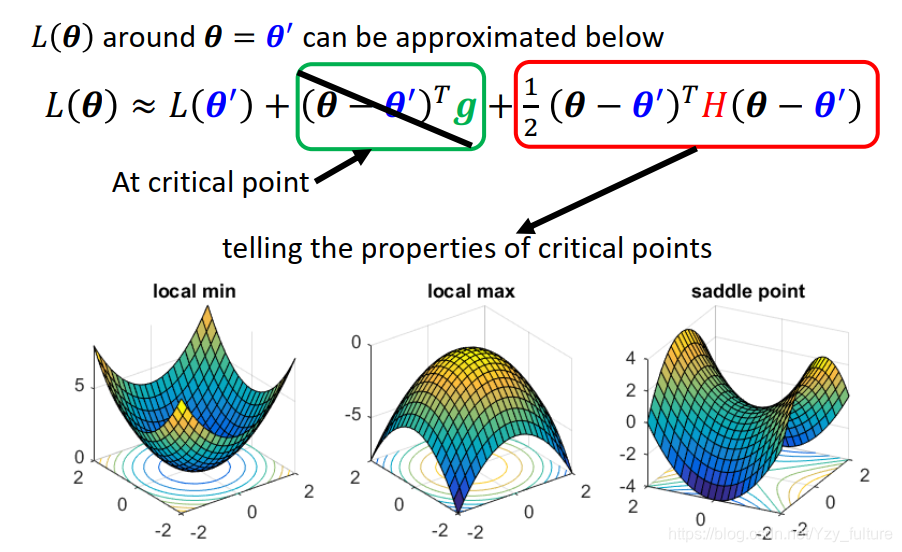
判断:通过hessian矩阵的特征值来判断- 特征值都为正的,则为local minima
- 特征值都为负的,则为local maxima
- 特征值一正一负,则为saddle point

若判断为saddle point,根据hessian矩阵进而看出更新的方向(负的特征值的方向),顺着方向走就可以让loss变小

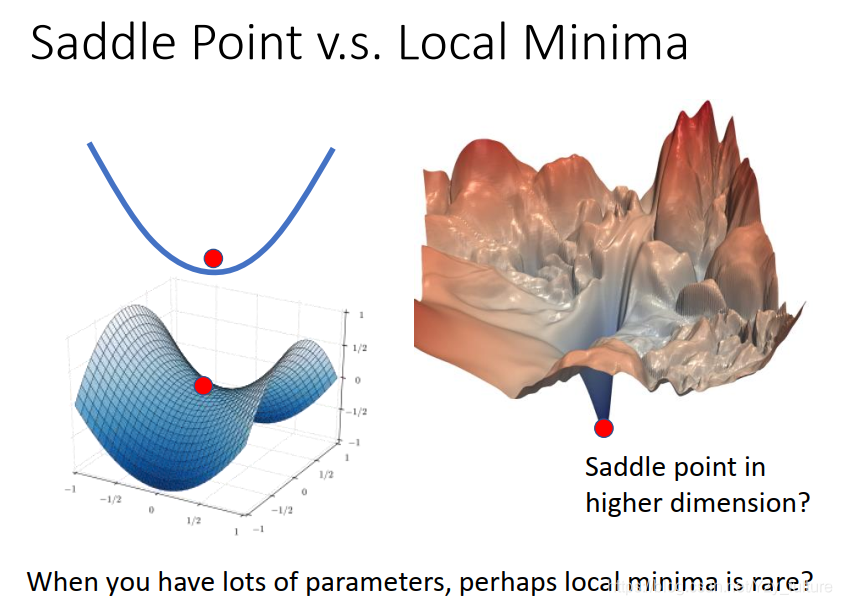
local minima和saddle point哪个更常见?
- 结论:saddle point更常见
- 原因:在当前维度的角度下是一个local minima,但放到更高维度的空间中有可能是一个saddle point
- 举例:在一维空间中都是local minima,但把它放到二维空间中它很可能是一个saddle point
2. 批次(batch)与动量(momentum)
2.1 批次(batch)
2.1.1 概述:
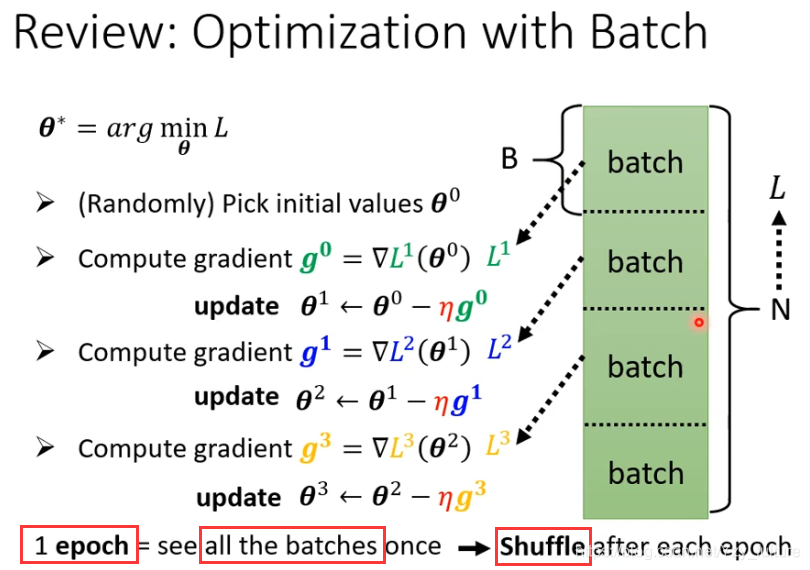
拿一个batch的资料拿出来算loss,所有的batch 看过一遍叫一个epoch
shuffle(洗牌) 有很多不同的做法,常见的做法是在每一次epoch开始之前会分一次batch,每一个epoch的batch都不一样。
2.1.2 为什么要用batch

- 左边(未用batch):看过所有的资料之后才能update一次
- 优点:稳妥
- 缺点:时间长
- 右边(使用batch,batch size = 1):看一个资料更新一次
- 优点:时间短
- 缺点:不稳妥
2.1.3 神奇之处:
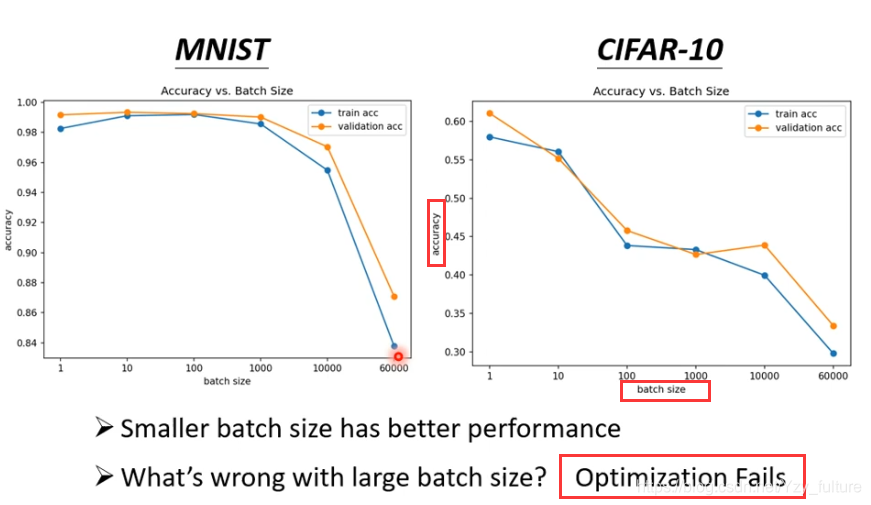
1.noisy的gradient 反而 可以帮助training
- 当你用大的batch size时,你的optimization可能会有问题。(model 一样,不是model bias的问题)
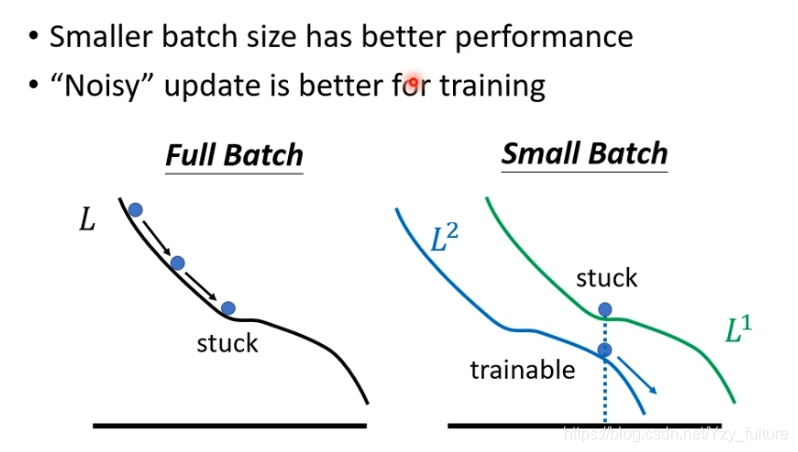
- 原因(一种解释):假设你是full batch 你在update你的参数的时候,就是沿着一个loss function来update参数,当走到一个local minima 显然就停下来了
但是假如是small batch 的话,因为我们是每次挑一个batch出来算它的 loss 。等于是你每次update 你的参数的时候,你用的loss function都是略有差异的。选到第一个batch的时候是用L1来算你的gradient ,选到第二个batch的时候是用L2来算你的gradient ,假设你用L1算 gradient 的时候发现是0卡住了,但L2它的function与L1又不一样,L1卡住了,L2不一定会卡住啊,所以L1卡住没关系,换下一个batch来 L2再算gradient,你还是有办法training你的model,还是有办法让你的loss变小。
2. 小的batch也对testing有帮助
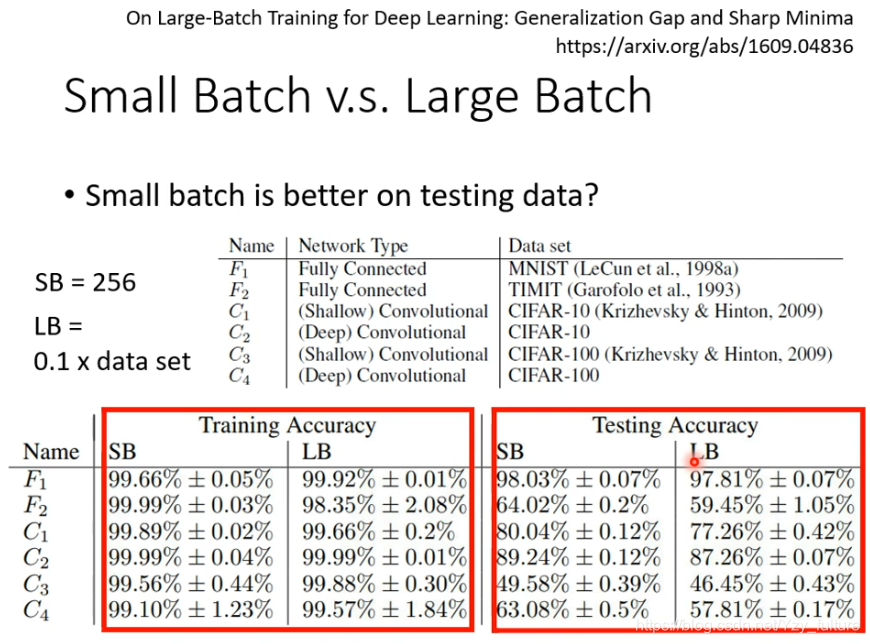
原因:在training loss上可能有很多个local minima,但local minima有好有坏,我们认为如果一个localminima 在一个峡谷里面,他就是一个坏的;在一个平原上,他就是一个好的。
因为training 和testing 之间会有差距,对“平原minima”来说,两者差的不会太多。“峡谷minima”就会差很多。
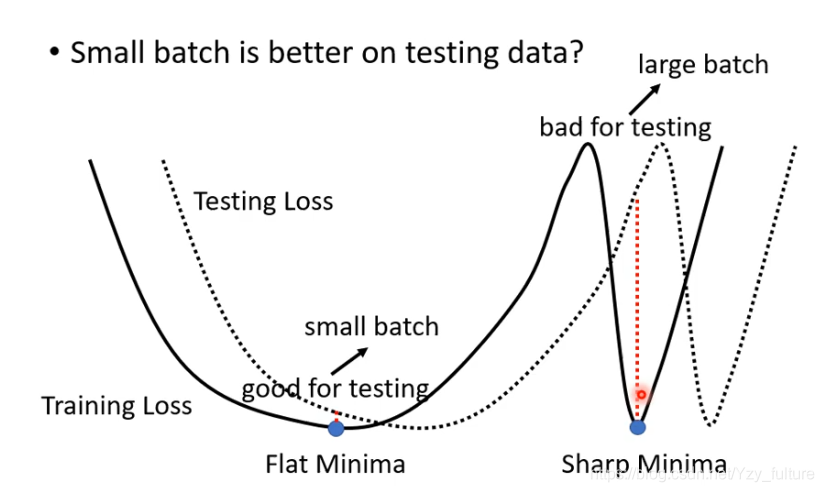
small batch or big batch

2.2 动量(momentum)
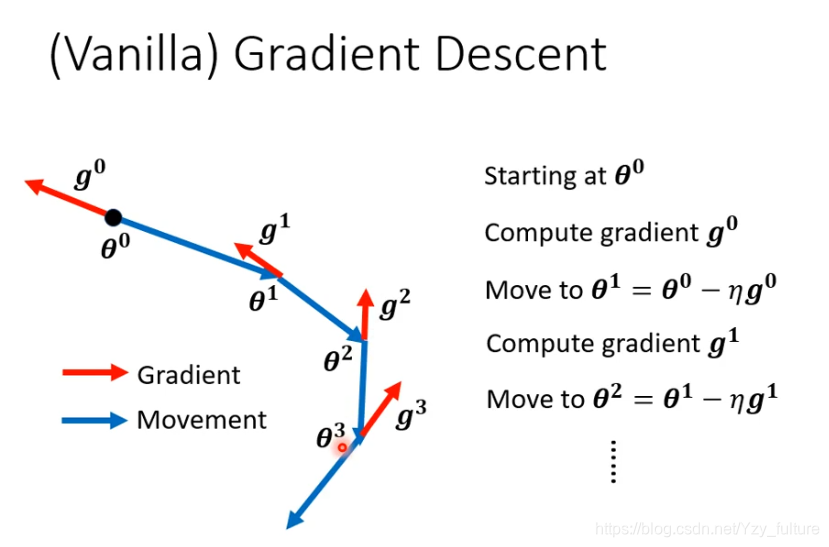
2.2.1 一般的gradient descent
有一个初始的参数
θ
0
\theta_{0}
θ0?计算该点gradient ,计算完之后往gradient的反方向去update参数,一直继续下去
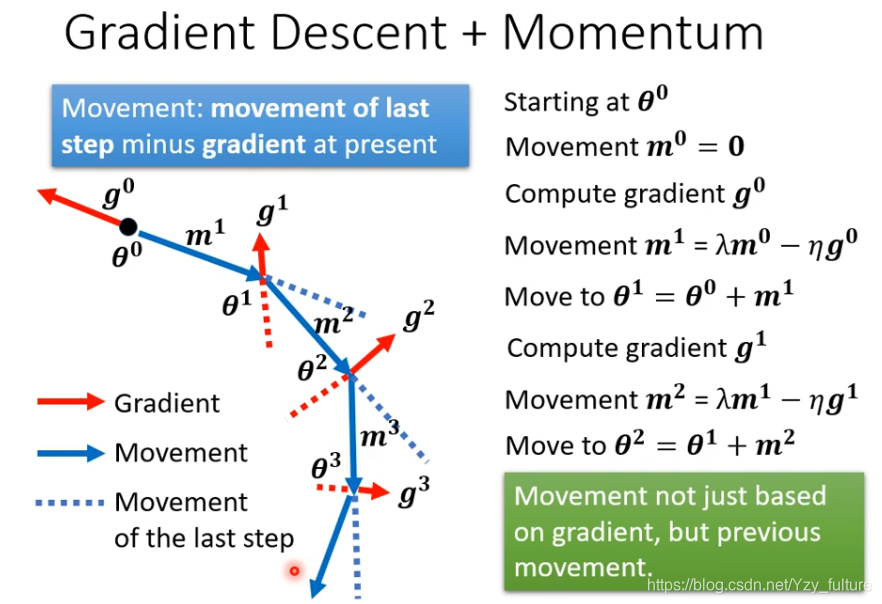
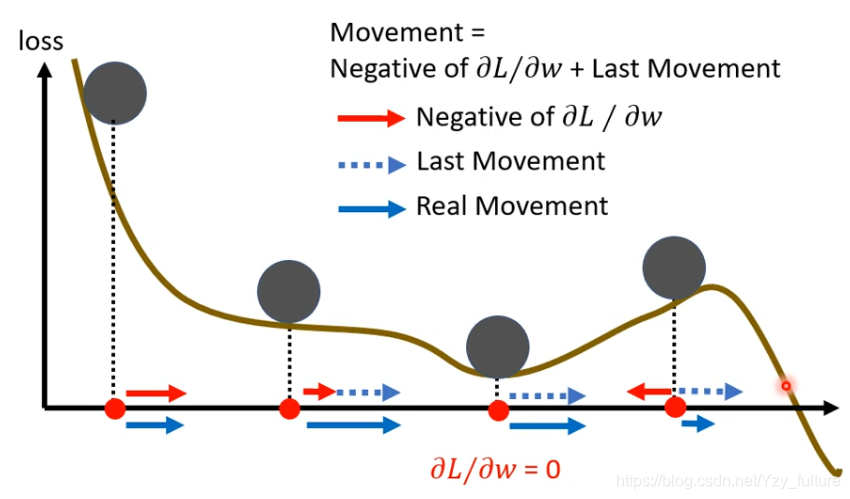
2.2.2 加上momentum
找一个初始参数,计算
g
0
g_0
g0?,下一步是gradient的方向加上前一步的方向

3. 自动调整学习率(Adaptive Learning Rate)
3.1 问题的引进
学过之前的东西,当loss不再发生变化的时候,你是否会认为此时一定到达critical point?你是否忘记了之前我们讨论学习率的时候那个学习率设置过大的后果?
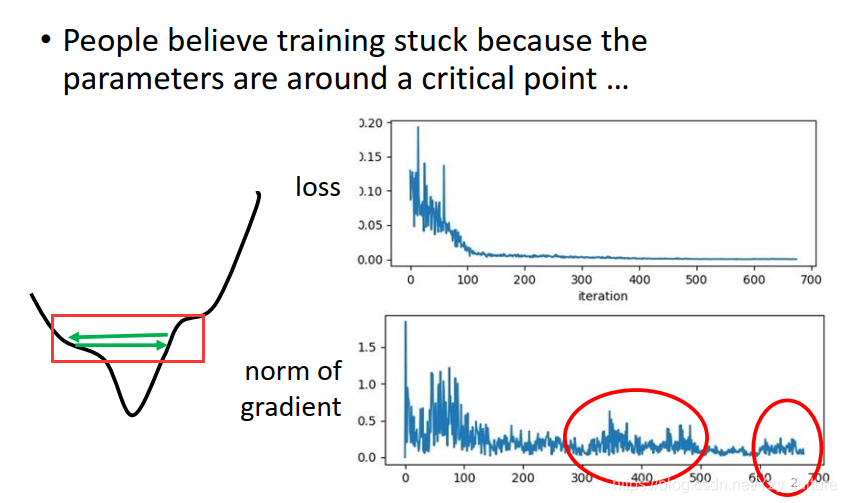
- 当学习率过大的时候,它为什么无法得到最优解呢?答案是:因为振荡
- 当学习滤过小的时候,因为步长过短,需要耗费的时间过长
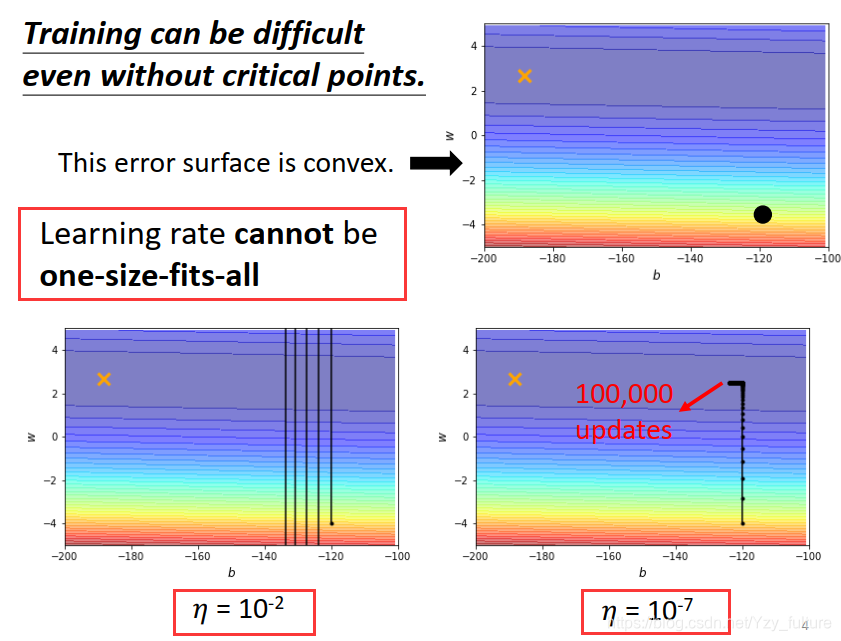
为了解决这个现象,我们来进行调整
3.2 修改学习率
- 原则:在坡度较大的地方,我们希望我们的步长小一点,此时我们应减小Learning Rate;在坡度较小的地方,我们希望我们的步长大一点,此时我们应增加Learning Rate
- 由原则的思想我们是否想到了之前谈论的进行学习率调整的adagrad算法,这个也就不在阐述。
在这里,我们要学会一个新的思路,那就是就算是同一个参数,他需要的学习率也会随时间而改变
RMS Prop
- 新增一个hyper parameter:
α
\alpha
α
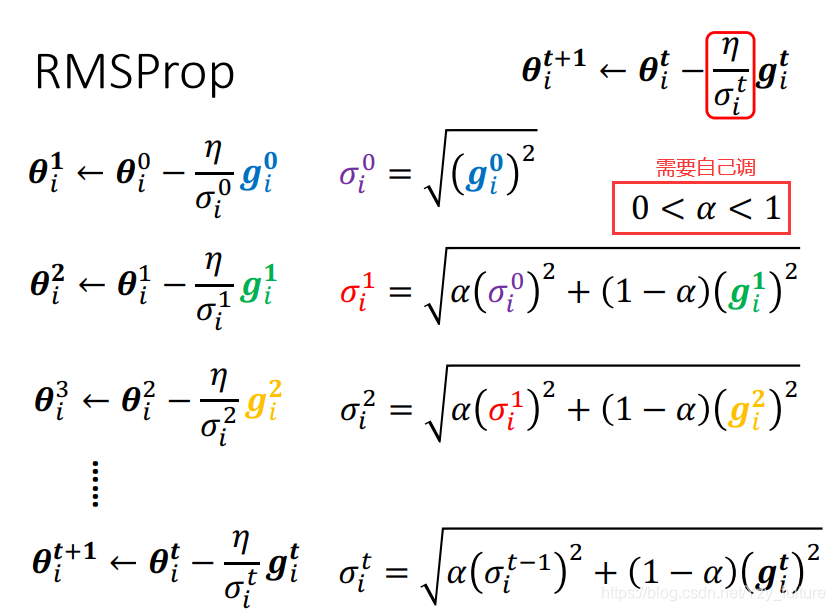
- 通过对
α
\alpha
α的调整来调整
g
i
1
g_i^{1}
gi1?的影响力大小。
- 若 α \alpha α趋于0,则 g i 1 g_i^{1} gi1?比较重要
- 若 α \alpha α趋于1,则 g i 1 g_i^{1} gi1?比较不重要,之前计算的gradient更加重要
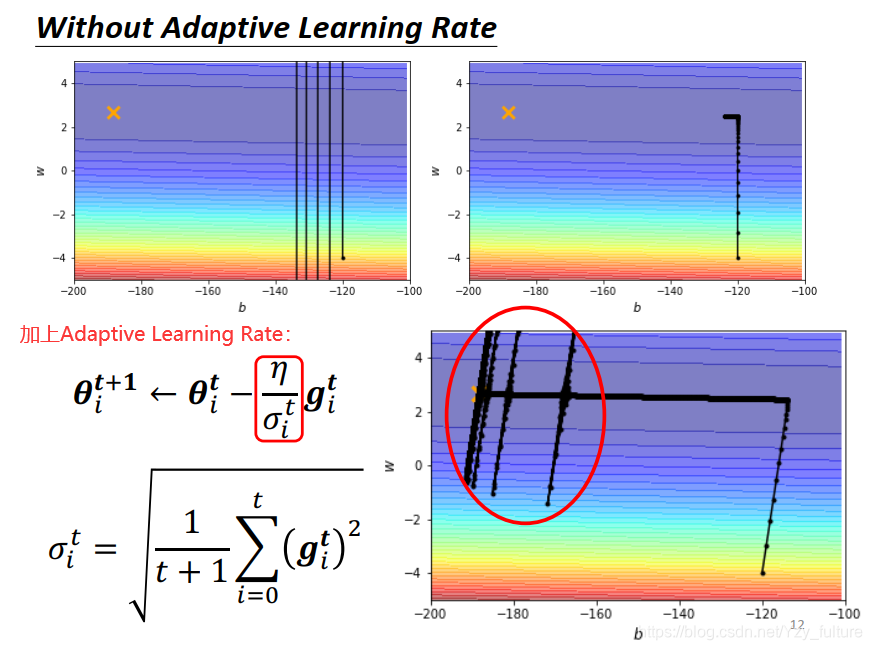
但可能会导致暴走的问题
3. 解决暴走的方法:
1. Learning Rate Scheduling:让
η
\eta
η与时间有关。随着时间的增加而让
η
\eta
η减小
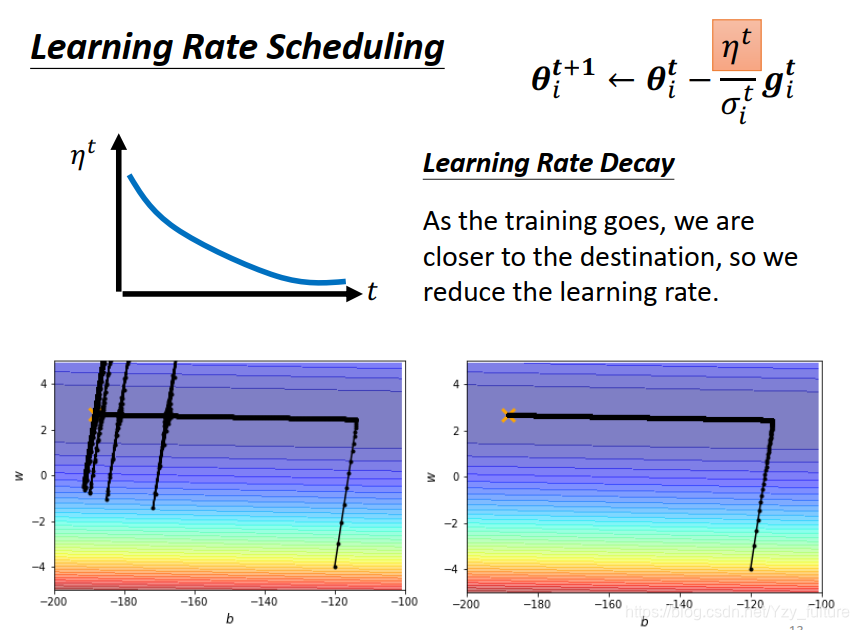
2. warm up

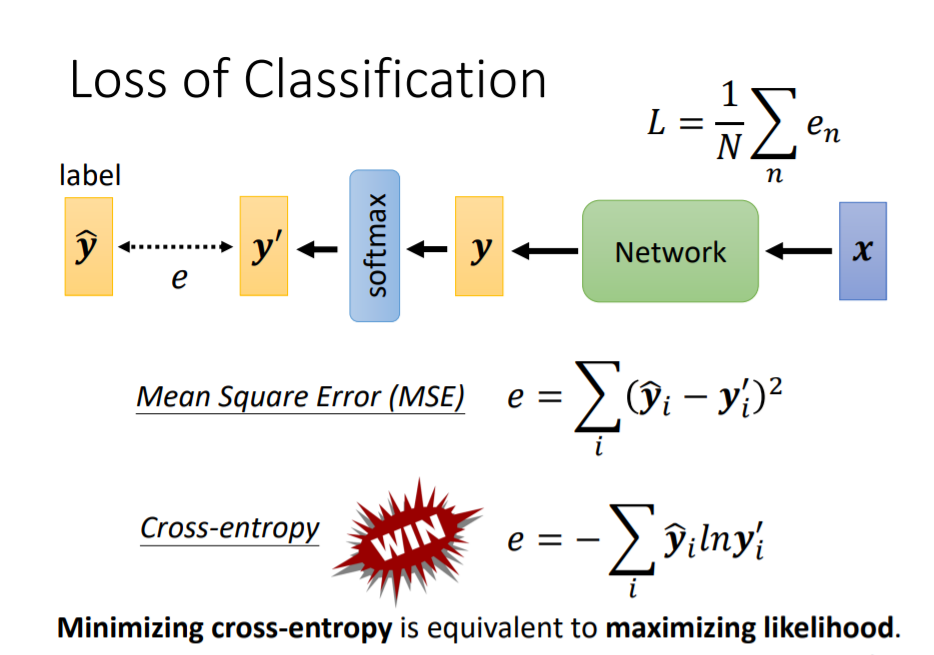
4. 损失函数也有影响
在做分类问题时,较多的把Class用独热向量来表示
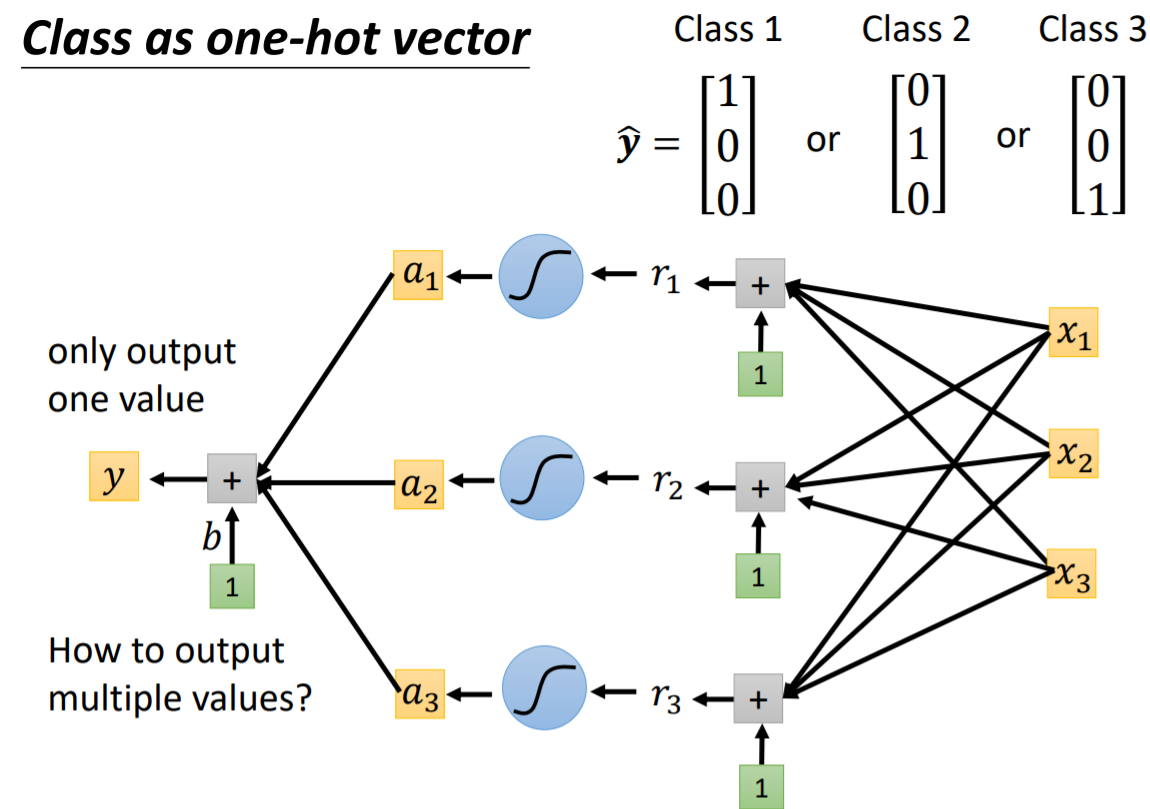
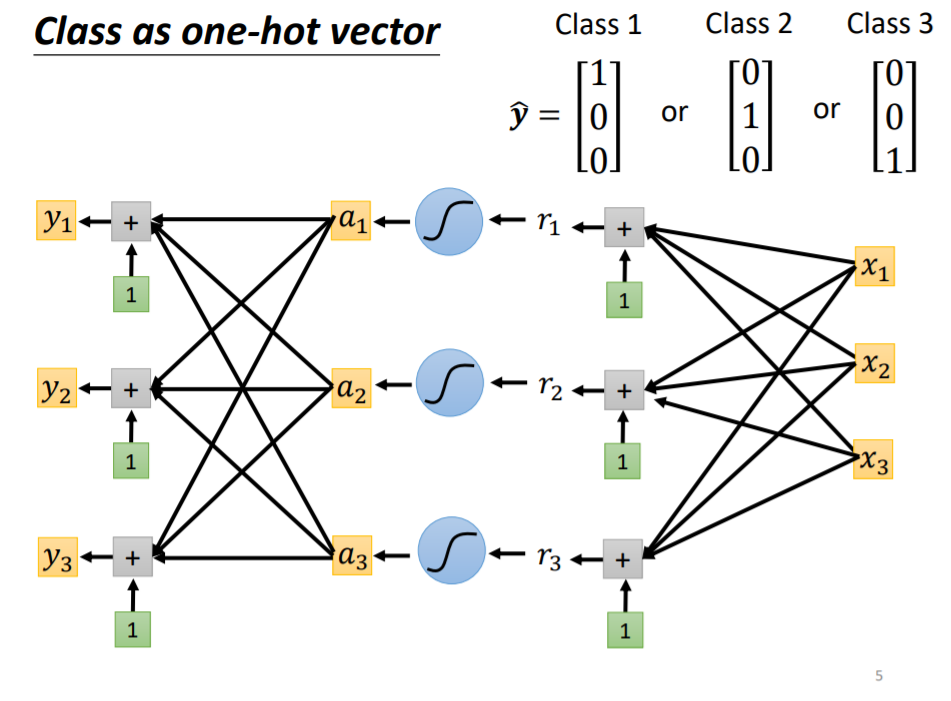

为了更好的使
y
^
\hat{y}
y^?和
y
′
y^{'}
y′接近,利用softmax来做处理:将
y
y
y中的值normallize移动到0-1,计算与label的相似度