
?一行表示一个样本,用(x1-x8)8个特征对这一个样本进行表示,特征的维度是一列



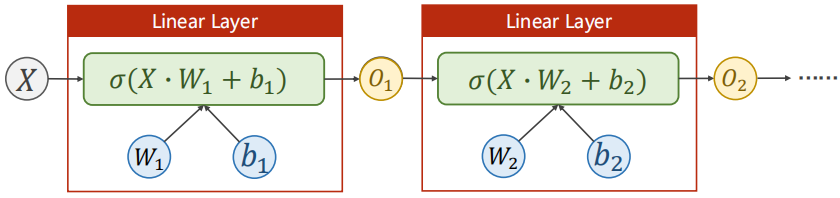
??(O即手写图中的Z)给Linear设置不同的输入、输出维度。
?把多个类似于logisc回归这种线性变换单元首尾相连,就能构造多层神经网络。

?矩阵的乘法运算,可以看作从N维空间映射到M维空间的线性变换。
?y = A * x
y:M × 1
A :M × N
x :N × 1
?神经网络的本质:寻找一种非线性的空间变换函数。(从N维→1维,通过引入Sigmoid激活函数给线性变换增加非线性因子)
神经网络到底设多少层,每层多少维,一般要通过超参数搜索的方法进行尝试,看什么样的设计在开发集表现比较好。
示例代码:
import numpy as np
import torch
import matplotlib.pyplot as plt
xy = np.loadtxt('diabetes.csv.gz', delimiter=',', dtype=np.float32)
x_data = torch.from_numpy(xy[:,:-1]) #:-1表示最后1列不要
y_data = torch.from_numpy(xy[:, [-1]]) #表示只取最后一列,并且是个矩阵类型
class Model(torch.nn.Module):
def __init__(self):
super(Model, self).__init__()
self.linear1 = torch.nn.Linear(8,6)
self.linear2 = torch.nn.Linear(6,4)
self.linear3 = torch.nn.Linear(4,1)
self.sigmoid = torch.nn.Sigmoid() #继承自Module,是一个模块
# self.activate = torch.nn.ReLU()
def forward(self,x):
x = self.sigmoid(self.linear1(x))
x = self.sigmoid(self.linear2(x))
x = self.sigmoid(self.linear3(x))
# x = self.activate(self.linear1(x))
# x = self.activate(self.linear2(x))
# x = self.activate(self.linear3(x))
return x
model = Model()
#criterion = torch.nn.BCELoss(size_average = True)
criterion = torch.nn.BCELoss(reduction='mean')
optimizer = torch.optim.SGD(model.parameters(), lr=0.1)
loss_list = []
epoch_list = []
for epoch in range(100):
#forward
epoch_list.append(epoch)
y_pred = model(x_data)
loss = criterion(y_pred, y_data)
print(epoch, loss.item())
loss_list.append(loss.item())
#backward
optimizer.zero_grad()
loss.backward()
#update
optimizer.step()
plt.plot(epoch_list, loss_list)
plt.xlabel('epoch')
plt.ylabel("loss")
plt.show()
np.loadtxt('diabetes.csv.gz', delimiter=',', dtype=np.float32) 第一个参数是这个数据集的路径,第二个参数是将数据以“,”分割,第三个参数是数据类型。
diabetes.csv.gz数据集链接:https://pan.baidu.com/s/1i064OJeghzyix0YyCMTDFw
提取码:8xla
输出结果:

使用如下代码来查看第一层或其他层的参数
layer1_weight = model.linear1.weight.data
layer1_bias = model.linear1.bias.data