自适应学习率:
今天介绍一种学习率调整的技术:自适应学习率。
相比前两章里提到的,利用均方根来对学习率进行调整,这里利用一种更新的方法来控制学习率,称为RMSProp,具体的数学过程如下:
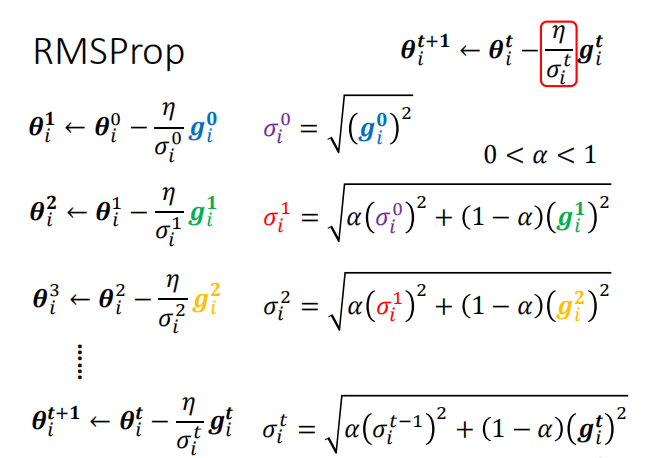

我们只需要对参数阿尔法进行调整,便可间接的调整学习率,从而控制下降步长。
论文参考:https://arxiv.org/pdf/1412.6980.pdf
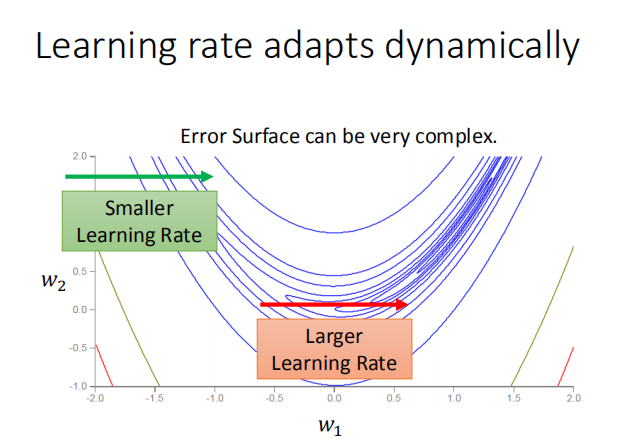
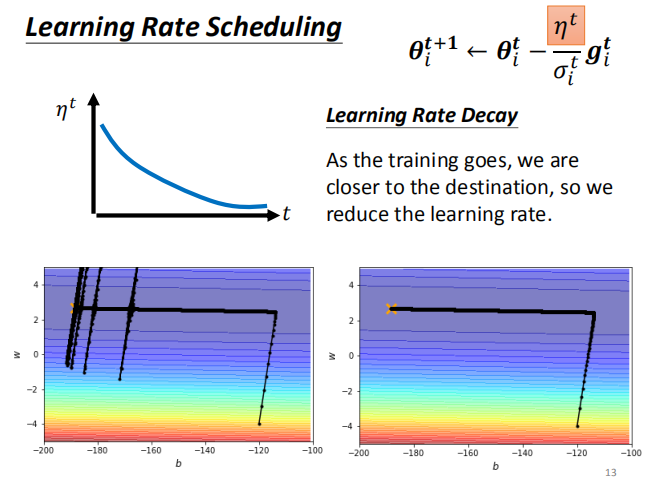
下图是利用均方根调整学习率,与自适应学习率的方法比较图:
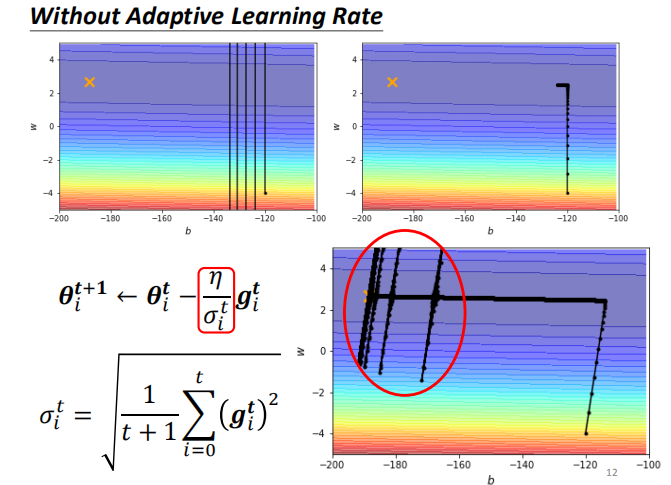
如上面两张图所示:图中的叉叉表示梯度下降的最低点,但不论我们如何调整学习率,也无法让其达到最低点。
如下图所示:我们利用了RMSProp技术,可见下降的效率相当之高,虽然有所波动,但确实达到了我们的最低点。为解决这种波动,通常情况下的处理手段是将学习率构造成与时间相关的函数,这就是:Learning Rate Decay,即学习率衰减。
分类:
我们在做分类的时候,常常需要把变量进行标签化,比如下图中的class
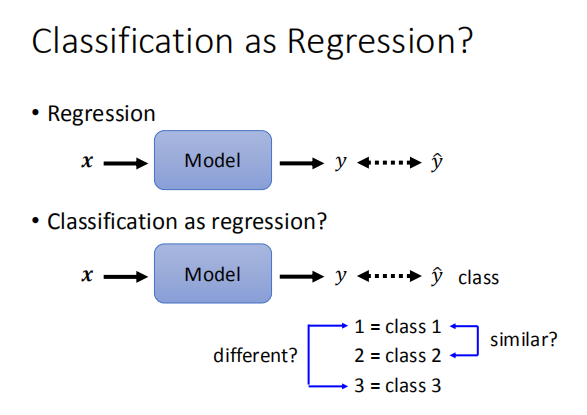
我们完全可以把class 1 记做1,class 2 记做2,以此类推。
但这里会面临一个问题,就是原来本来无关的变量,在进行转换后似乎有了某种关系,比如这里的class1与class2是无关的,但它们变成1,2后,似乎就有了大小的意味,或者班级2是班级1的两倍这种不合理的关系。所以通常的办法是交给one-hot-vector去做:
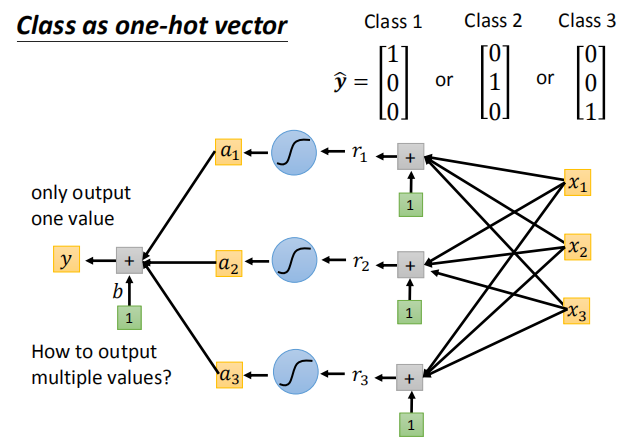
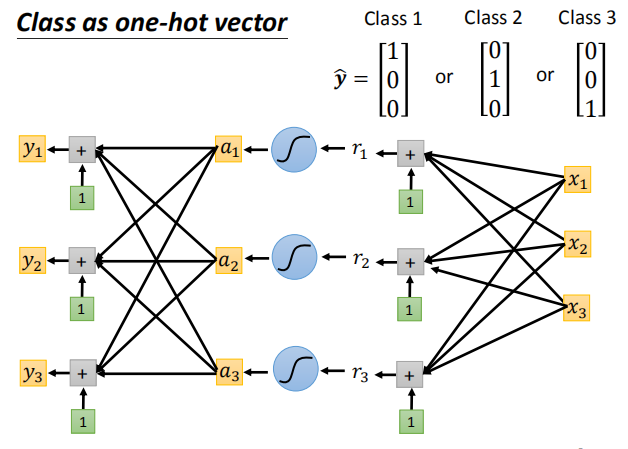
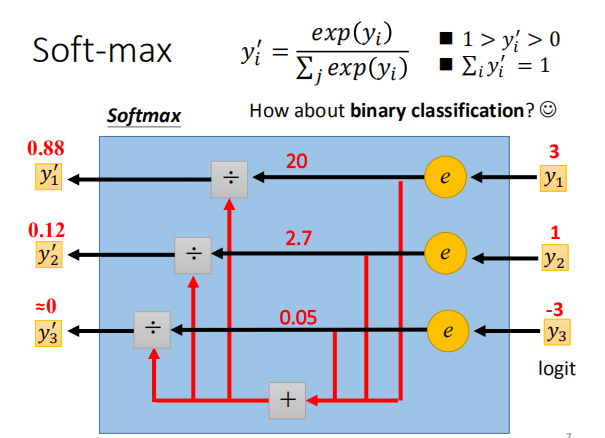
那对于二分类问题呢?我们利用soft-max去做,具体原理如下: