[人工智能]李宏毅《深度学习》（五）

人工智能的浪潮正在席卷全球，诸多词汇时刻萦绕在我们耳边：人工智能（Artificial Intelligence）、机器学习（Machine Learning）、深度学习（Deep Learning）。本文主要是对李宏毅课程内容进行笔记梳理，参考链接在文末已经给出。

6-batchsize

目前深度学习模型多采用批量随机梯度下降算法进行优化，随机梯度下降算法的原理如下:

$w_{t+1}=w_t?\eta \frac{1}{n}{\sum }_{i\in ?}?l(x,w_t)$

n是批量大小(batchsize)，η是学习率(learning rate)。可知道除了梯度本身，这两个因子直接决定了模型的权重更新，从优化本身来看它们是影响模型性能收敛最重要的参数。

学习率直接影响模型的收敛状态，batchsize则影响模型的泛化性能，两者又是分子分母的直接关系，相互也可影响。

大的batchsize减少训练时间，提高稳定性

模型性能对batchsize虽然没有学习率那么敏感，但是在进一步提升模型性能时，batchsize就会成为一个非常关键的参数。

同样的epoch数目，大的batchsize需要的batch数目减少了，所以可以减少训练时间，目前已经有多篇公开论文在1小时内训练完ImageNet数据集。另一方面，大的batch size梯度的计算更加稳定，因为模型训练曲线会更加平滑。在微调的时候，大的batch size可能会取得更好的结果。

batchsize在变得很大(超过一个临界点)时，会降低模型的泛化能力。在此临界点之下，模型的性能变换随batch size通常没有学习率敏感。

7-动量（momentum）

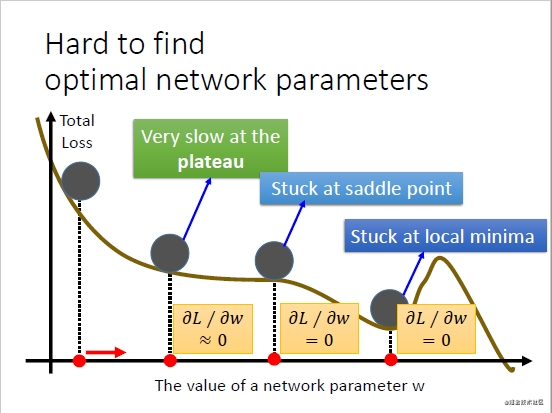
我们使用SGD（stochastic mini-batch gradient descent，深度学习中一般称之为SGD）训练参数时，有时候会下降的非常慢，并且可能会陷入到局部最小值中，如下图所示

动量的引入就是为了加快学习过程，特别是对于高曲率、小但一致的梯度，或者噪声比较大的梯度能够很好的加快学习过程。动量的主要思想是积累了之前梯度指数级衰减的移动平均（前面的指数加权平均），下面用一个图来对比下，SGD和动量的区别：

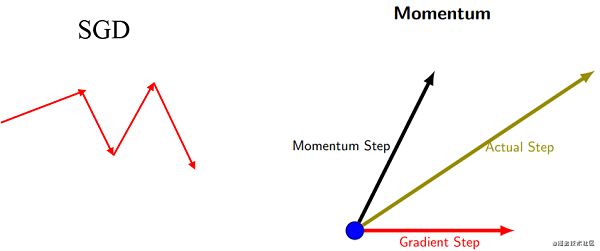
区别： SGD每次都会在当前位置上沿着负梯度方向更新（下降，沿着正梯度则为上升），并不考虑之前的方向梯度大小等等。而动量（moment）通过引入一个新的变量 v vv 去积累之前的梯度（通过指数衰减平均得到），得到加速学习过程的目的。

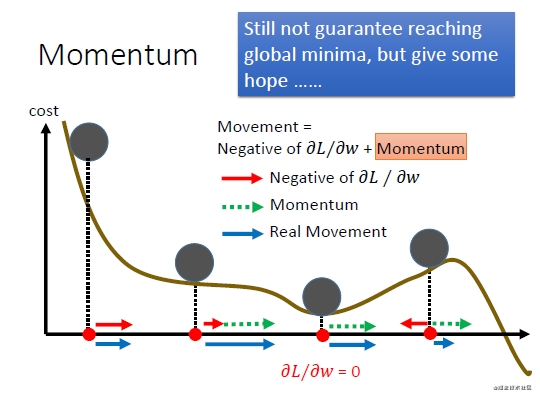
最直观的理解就是，若当前的梯度方向与累积的历史梯度方向一致，则当前的梯度会被加强，从而这一步下降的幅度更大。若当前的梯度方向与累积的梯度方向不一致，则会减弱当前下降的梯度幅度。

用一个图来形象的说明下上面这段话

下面给出动量（momentum）的公式：

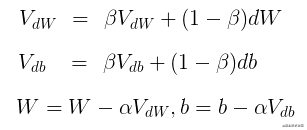
β的值越大，则之前的梯度对现在的方向影响越大。β一般取值为0.5, 0.9, 0.99。推荐取值0.9。

8-学习率

初始学习率大小对模型性能的影响

初始的学习率肯定是有一个最优值的，过大则导致模型不收敛，过小则导致模型收敛特别慢或者无法学习，下图展示了不同大小的学习率下模型收敛情况的可能性。

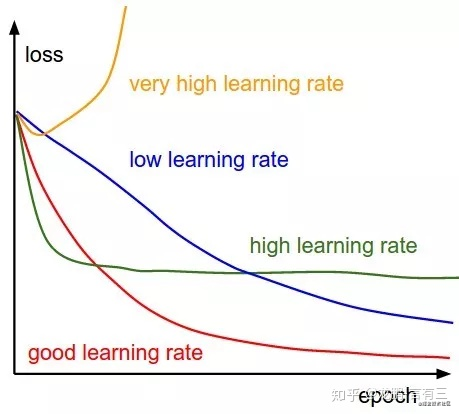
那么在不考虑具体的优化方法的差异的情况下，怎样确定最佳的初始学习率呢？

通常可以采用最简单的搜索法，即从小到大开始训练模型，然后记录损失的变化，通常会记录到这样的曲线。

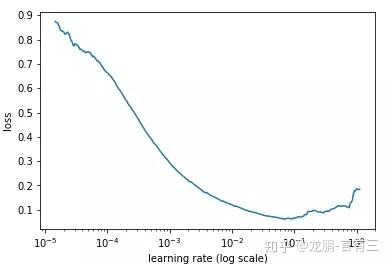
随着学习率的增加，损失会慢慢变小，而后增加，而最佳的学习率就可以从其中损失最小的区域选择。

有经验的工程人员常常根据自己的经验进行选择，比如0.1，0.01等。

学习率变换策略对模型性能的影响

学习率在模型的训练过程中很少有不变的，通常会有两种方式对学习率进行更改，一种是预设规则学习率变化法，一种是自适应学习率变换方法。

预设规则学习率变化法

常见的策略包括fixed，step，exp，inv，multistep，poly，sigmoid等，集中展示如下：

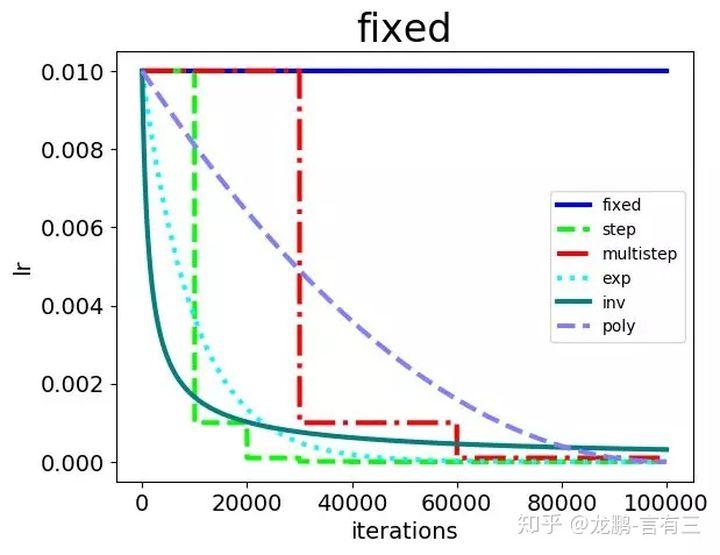
• step，multistep方法的收敛效果最好，这也是我们平常用它们最多的原因。虽然学习率的变化是最离散的，但是并不影响模型收敛到比较好的结果。
• 其次是exp，poly。它们能取得与step，multistep相当的结果，也是因为学习率以比较好的速率下降，虽然变化更加平滑，但是结果也未必能胜过step和multistep方法，在这很多的研究中都得到过验证，离散的学习率变更策略不影响模型的学习。
• inv和fixed的收敛结果最差。这是比较好解释的，因为fixed方法始终使用了较大的学习率，而inv方法的学习率下降过程太快。

对于采用非自适应学习率变换的方法，学习率的绝对值对模型的性能有较大影响，研究者常使用step变化策略。

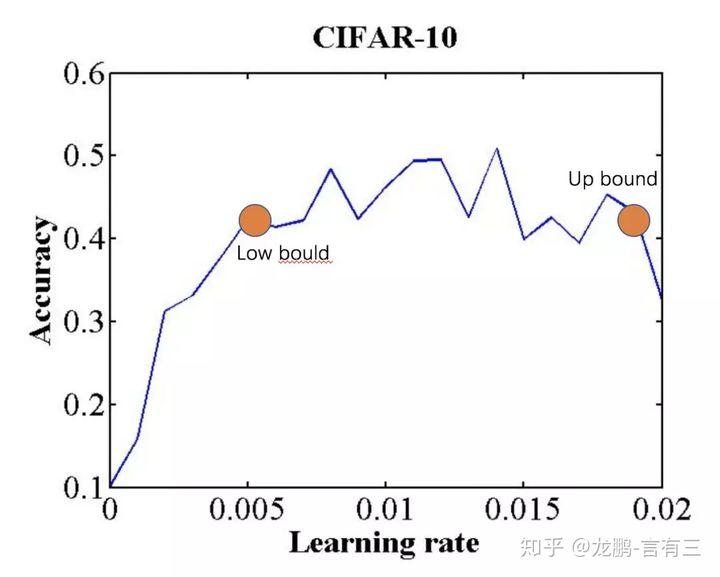
目前学术界也在探索一些最新的研究方法，比如cyclical learning rate，示意图如下：

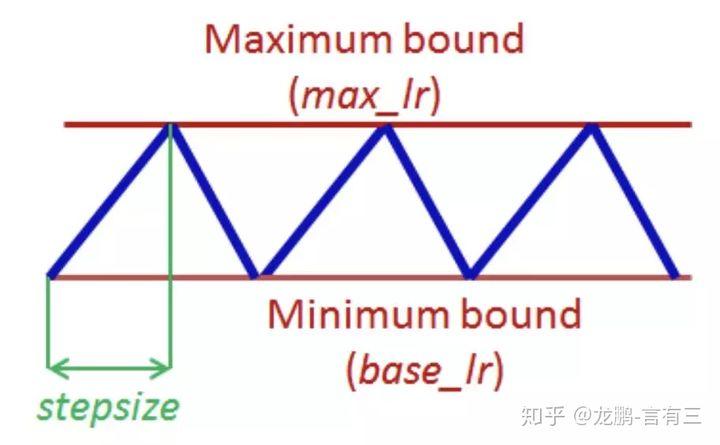
实验证明通过设置上下界，让学习率在其中进行变化，可以在模型迭代的后期更有利于克服因为学习率不够而无法跳出鞍点的情况。

确定学习率上下界的方法则可以使用LR range test方法，即使用不同的学习率得到精度曲线，然后获得精度升高和下降的两个拐点，或者将精度最高点设置为上界，下界设置为它的1/3大小。

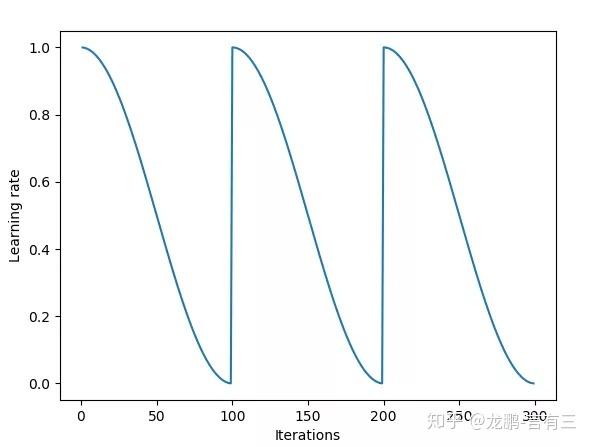
SGDR方法则是比cyclical learning rate变换更加平缓的周期性变化方法，如下图，效果与cyclical learning rate类似。

自适应学习率变换方法

最常用的优化的策略就是Adam。

Adam (Kingma and Ba, 2014) 是另一种学习率自适应的优化算法，如图所示。 “Adam” 这个名字派生自短语 “adaptive moments”。早期算法背景下，它也许最好被看作结合 RMSProp 和具有一些重要区别的动量的变种。首先，在 Adam 中，动量直接并入了梯度一阶矩（指数加权）的估计。将动量加入 RMSProp 最直观的方法是将动量应用于缩放后的梯度。结合缩放的动量使用没有明确的理论动机。其次， Adam 包括偏置修正，修正从原点初始化的一阶矩（动量项）和（非中心的）二阶矩的估计。 RMSProp 也采用了（非中心的）二阶矩估计，然而缺失了修正因子。因此，不像 Adam，RMSProp 二阶矩估计可能在训练初期有很高的偏置。Adam 通常被认为对超参数的选择相当鲁棒，尽管学习率有时需要从建议的默认修改。

9-损失函数的影响

当在做分类问题的时候，比较常见的是把Class用one - hot vector表示

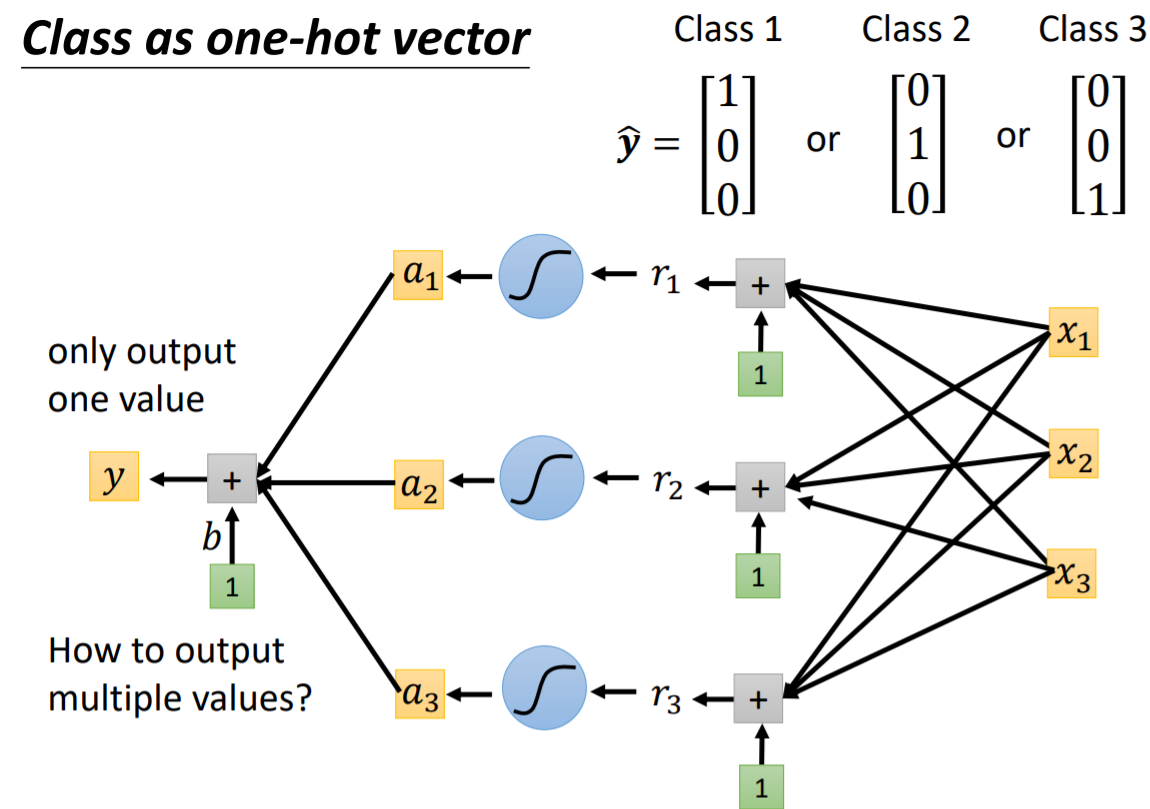
离散特征的编码分为两种情况：

1、离散特征的取值之间没有大小的意义，比如color：[red,blue],那么就使用one-hot编码

2、离散特征的取值有大小的意义，比如size:[X,XL,XXL],那么就使用数值的映射{X:1,XL:2,XXL:3}

其中独热编码即 One-Hot 编码，又称一位有效编码，其方法是使用N位状态寄存器来对N个状态进行编码，每个状态都由他独立的寄存器位，并且在任意时候，其中只有一位有效。

例如：

自然状态码为：000,001,010,011,100,101

独热编码为：000001,000010,000100,001000,010000,100000

可以这样理解，对于每一个特征，如果它有m个可能值，那么经过独热编码后，就变成了m个二元特征（如成绩这个特征有好，中，差变成one-hot就是100, 010, 001）。并且，这些特征互斥，每次只有一个激活。因此，数据会变成稀疏的。

这样做的好处主要有：

1. 解决了分类器不好处理属性数据的问题
2. 在一定程度上也起到了扩充特征的作用

实现方法一：pandas之get_dummies方法

pandas.get_dummies(data, prefix=None, prefix_sep='_', dummy_na=False, columns=None, sparse=False, drop_first=False)

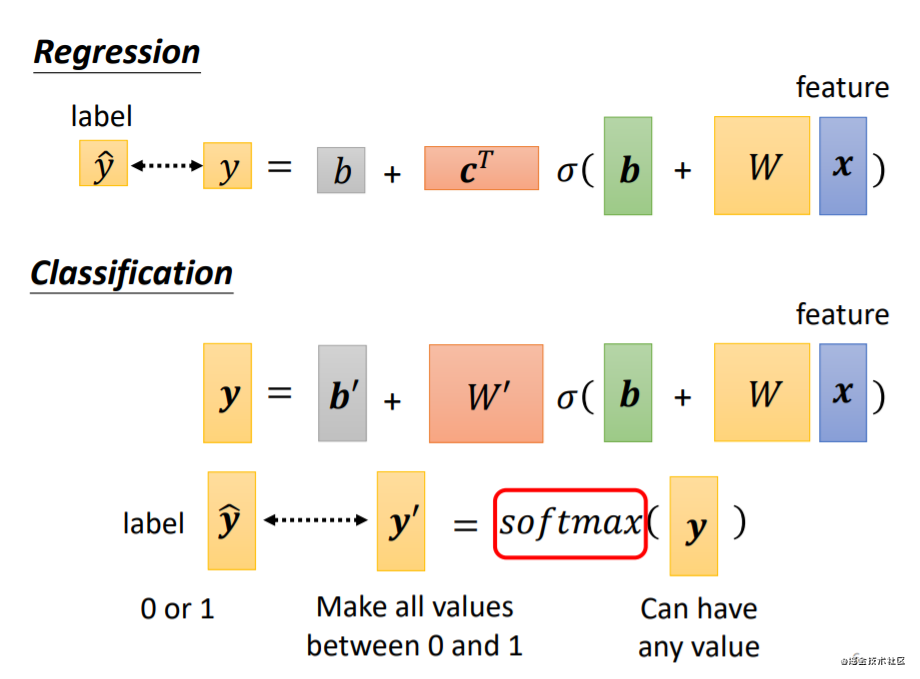
要让$y$—$y^{\prime }$接近，就需要利用 softmax 来做处理：将y中的值Normalize，移动到0 -1 之间，这样才好和label计算相似度。

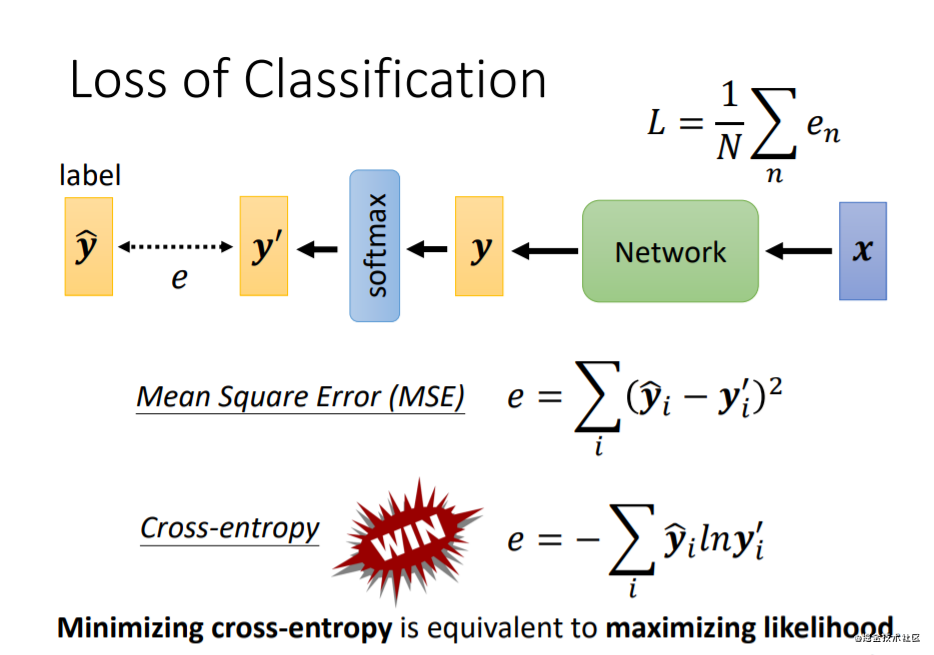
Cross - entropy比Mean Square Error更加适合用在分类上；而 Cross - entropy 相比 Mean Square Error 更常用在classification上，但这两者又经常一起使用。

在没有好的optimizer的情况下，使用MSE 可能会导致模型训练不起来。

参考链接：

• 链接：https://zhuanlan.zhihu.com/p/64864995