网络设计技巧
类神经网络训练不起来怎么办(一)局部最小值与鞍点
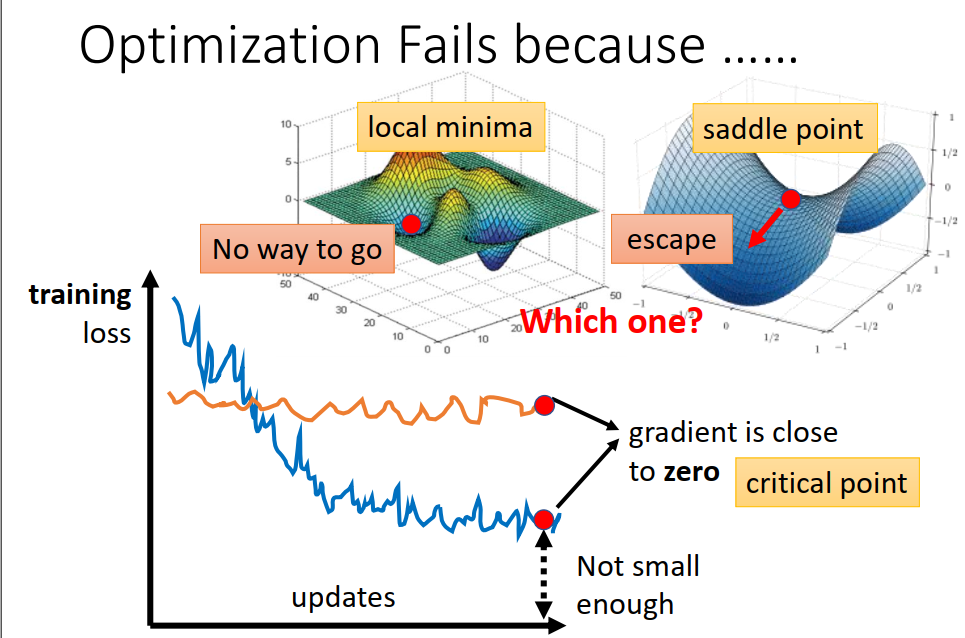
如何分辨到底是卡在local minima 还是 saddle point?
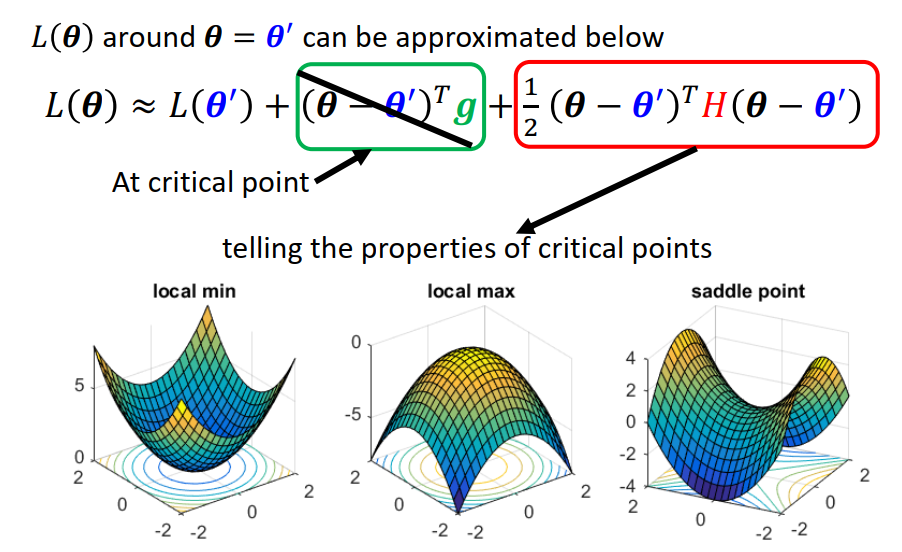
L (θ) loss function 在 θ’ 附近的泰勒展开式,
其中 gradient是一个向量,弥补 θ和θ’ 之间的差距;
hessian是一个矩阵,会补足加上gradient后与真正的L (θ) 之间的差距。

如果走到了一个critical point,意味着gradient为0,即绿色这一项为0 ,只剩下红色这一项。
为了方便,将(θ - θ’)设为 v
只需要看H的 eigenvalue(特征值)的正负即可。
H的特征值全为正的时候 ,我们认为是 local minima
H的特征值全为负的时候 ,我们认为是 local maxima
H的特征值有正有负时候 ,我们认为是 saddle point

如果训练停下来是因为saddle point ,我们可以继续看hessian 进而看出 update 的方向。
找出负的特征值(saddle point 特征值有正有负)顺着 u 的方向更新,就可以让loss变小。

注:在实际的 implementation 里面,你几乎不会真的把hessian算出来,运算量非常非常的大。
后续会谈到其他的逃离saddle point的方法 他们的运算量都要比算H小的多,之所以讲这个方法,
是因为如果卡在saddle point 也许没那么可怕,至少我们还有这一招。
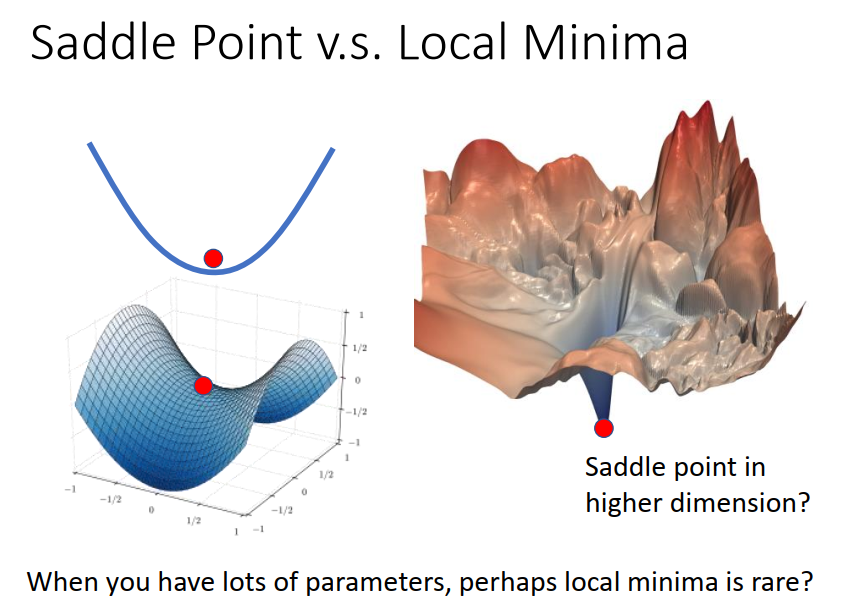
saddle point 跟local minima 哪个更常见?
先给出答案 saddle point更常见,local minima 很少很少
解释:在一维的空间好像到处都是local minima ,但是 会不会在二维空间来看他就是一个saddle point,当前维度空间看是一个local minima 但在更高维的空间中有可能就是一个saddle point。
今天我们训练一个network时候,参数往往动辄百万千万以上,我们的参数有多少就代表我们的error surface的维度有多少,既然维度这么高,会不会其实根本就有非常多的路可以走?既然有非常多的路可以走,会不会其实local minima根本就很少呢!如果你做一些实验,结果也是支持这一假设!
类神经网络训练不起来怎么办(二)批次与动量
批次(batch)与动量(momentum)
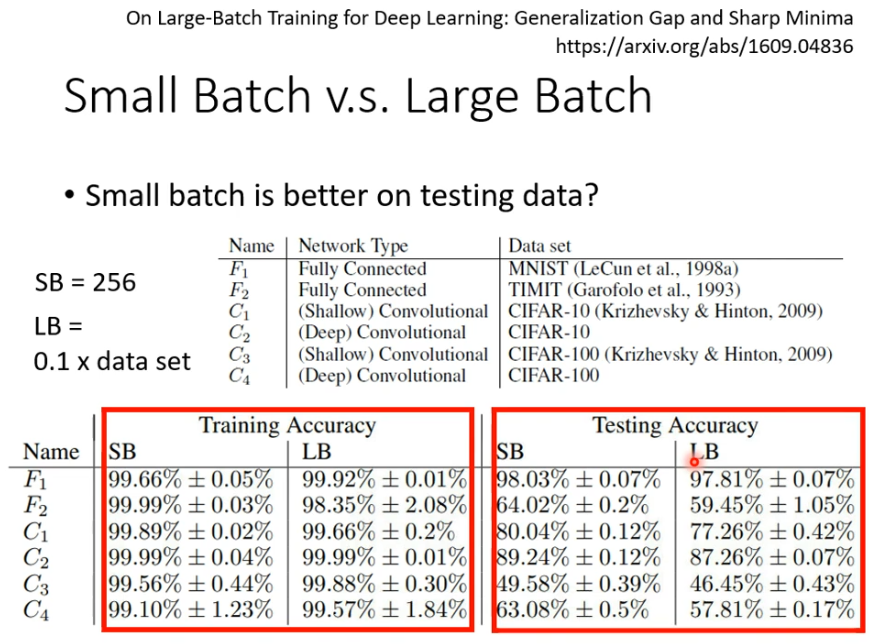
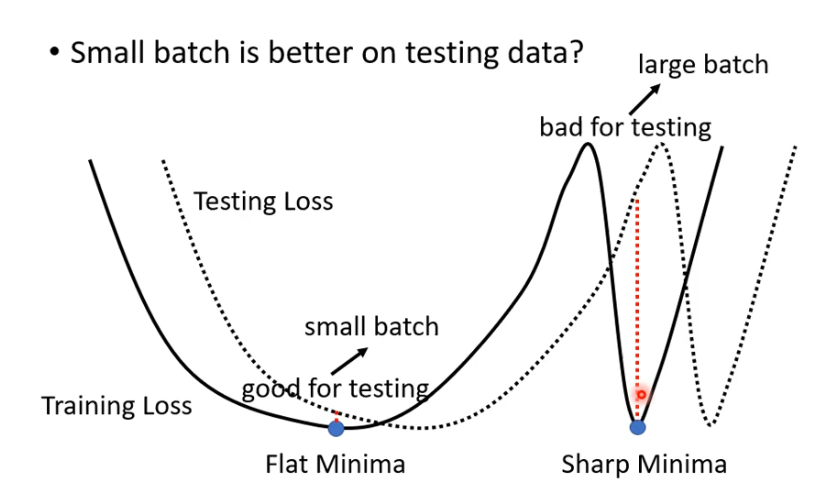
两个有可能可以对抗 saddle point 或local minima 的技术。
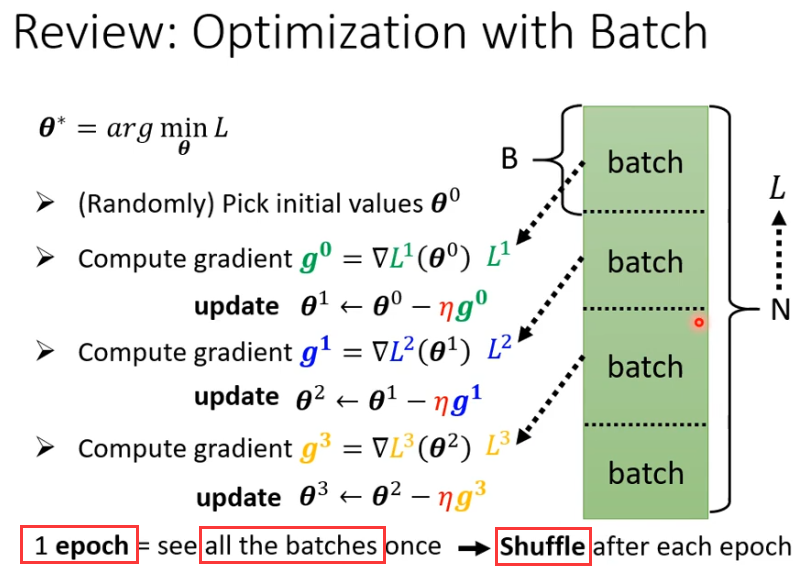
Batch
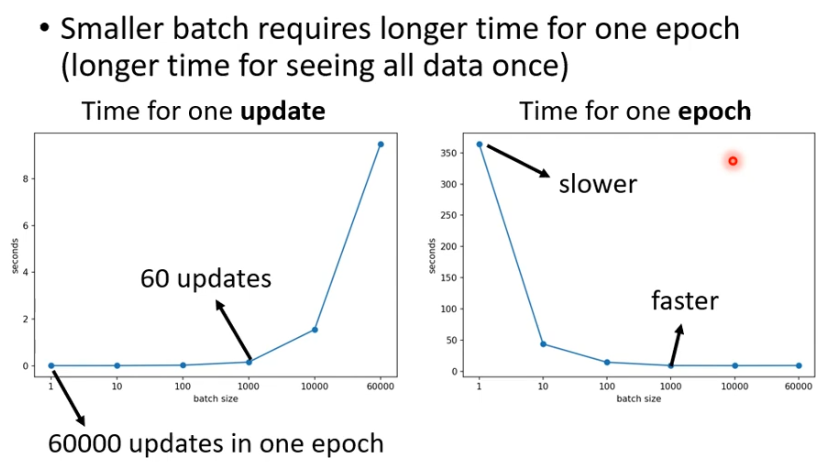
拿一个batch的资料拿出来算loss,所有的batch 看过一遍叫一个epoch
shuffle(洗牌) 有很多不同的做法,常见的做法是在每一次epoch开始之前会分一次batch,每一个epoch的batch都不一样。

类神经网络训练不起来怎么办(三)自动调整学习率
自动调整学习速率:Adaptive Learning Rate
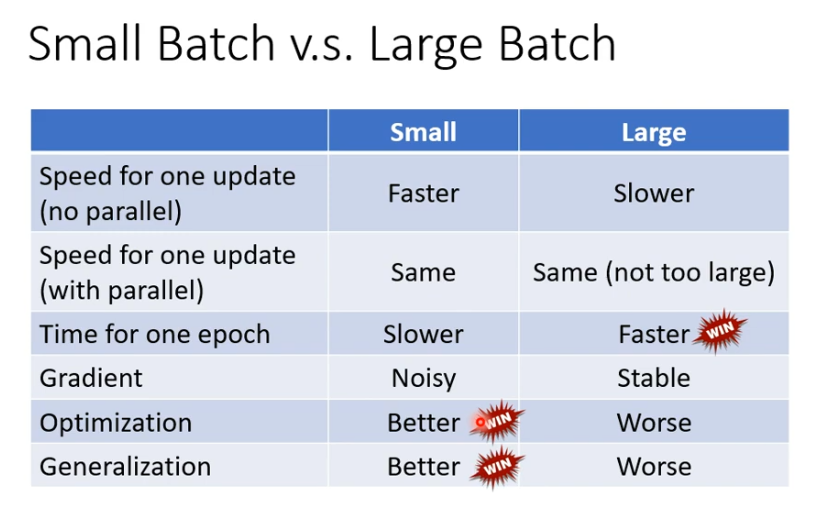
critical point 不一定是我们训练过程中最大的阻碍。
往往在训练一个network时,我们会把它的loss记录下来,通常随着参数update的次数增加loss会减小,最后就卡住了,多数时候,大家就会猜说是不是走到了critical point,因为gradient = 0 ,没法更新参数。但你真的确认过,当loss无法在下降的时候,gradient 真的很小吗?
比如下面这个例子,当训练终止的时候,loss几乎已经不动了,gradient 却在反复振荡。
可能是现在的gradient在error surface 山谷的的两个谷壁间反复振荡,这时loss不会再下降,但gradient却不是最小。(步幅太大,没法掉下去)
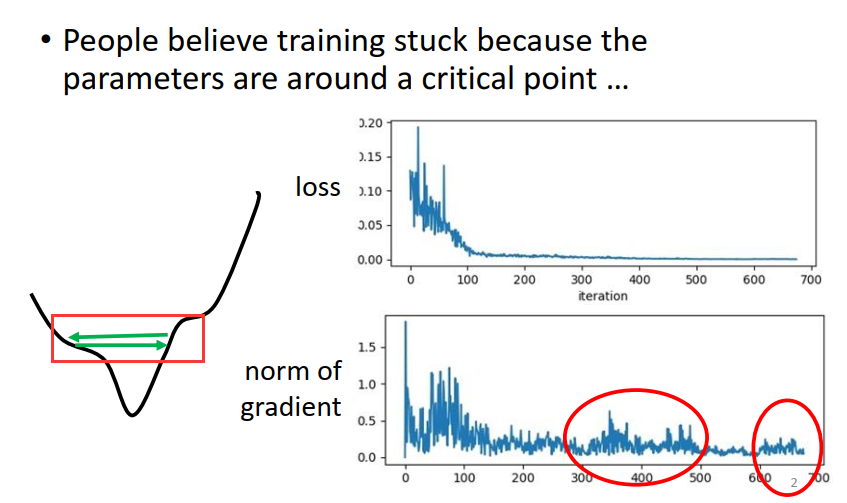
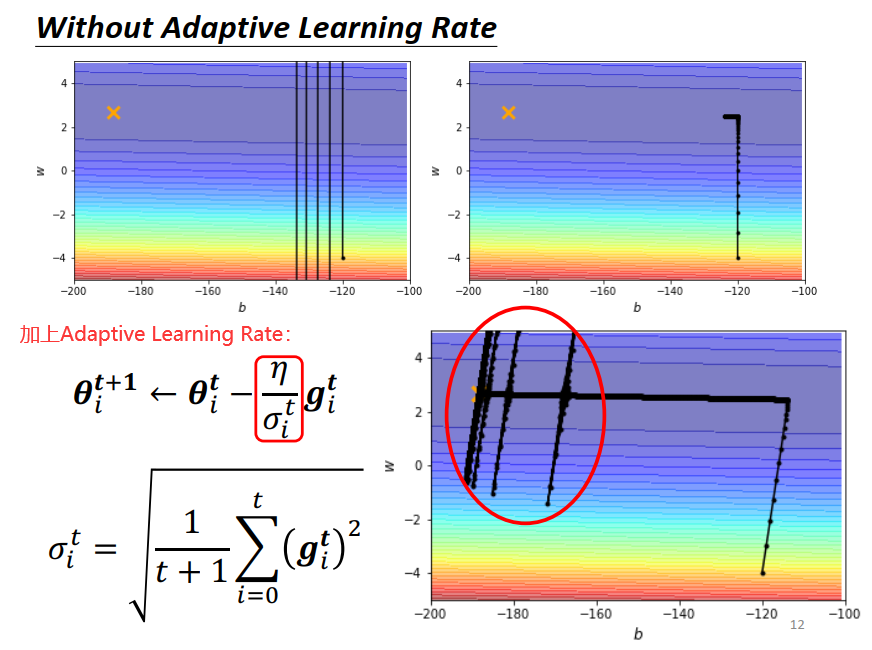
如果gradient descend 所有的参数都设同样的learning rate 会出现下面的情况:步幅过大,无法得到较小的loss,步幅过小无法逼近local minima的点。
当我们遇到更复杂的error surface ,真的要training一个 deep network 的时候,gradient descend 或许是你唯一可以依赖的工具。
但这么简单的问题(上图) gradient descend 都做不好,更难的问题它又怎么可能做好呢?
所以我们需要更好的gradient descend 的版本 – learning rate 为每一个参数定制化。
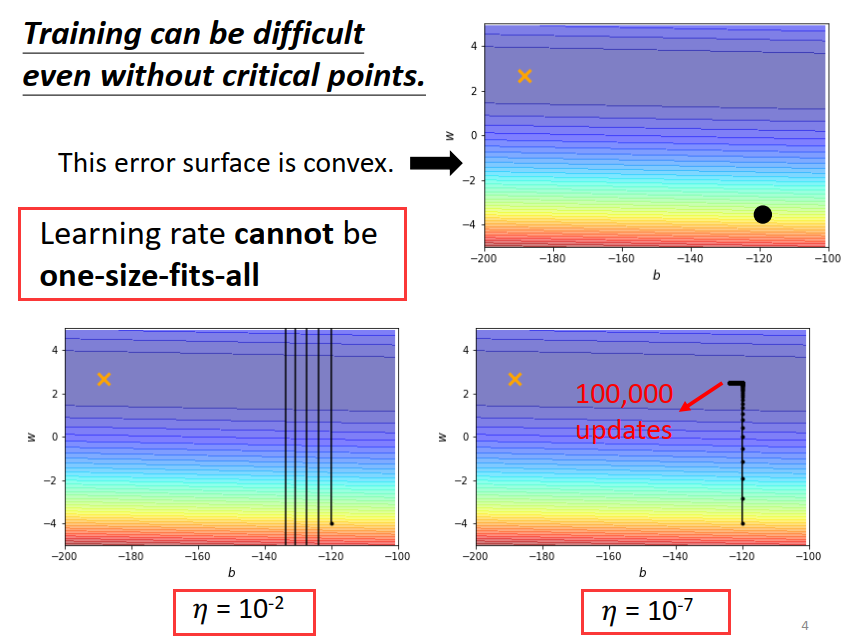
一个大的原则是:如果某一方向上坡度很大,我们其实希望learning rate 可以小一点;
? 如果某一方向上坡度很小,我们可以让learning rate 大一点。
改进方案:修改学习率
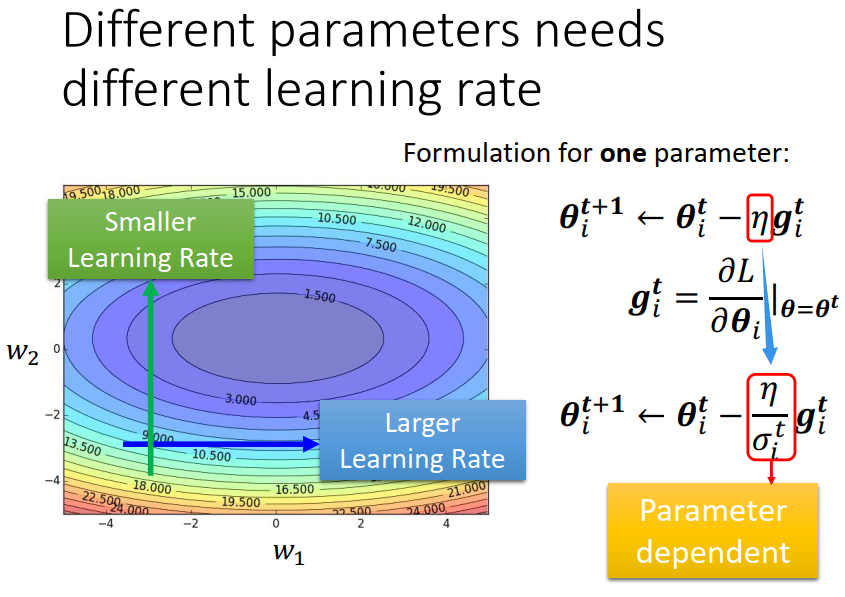
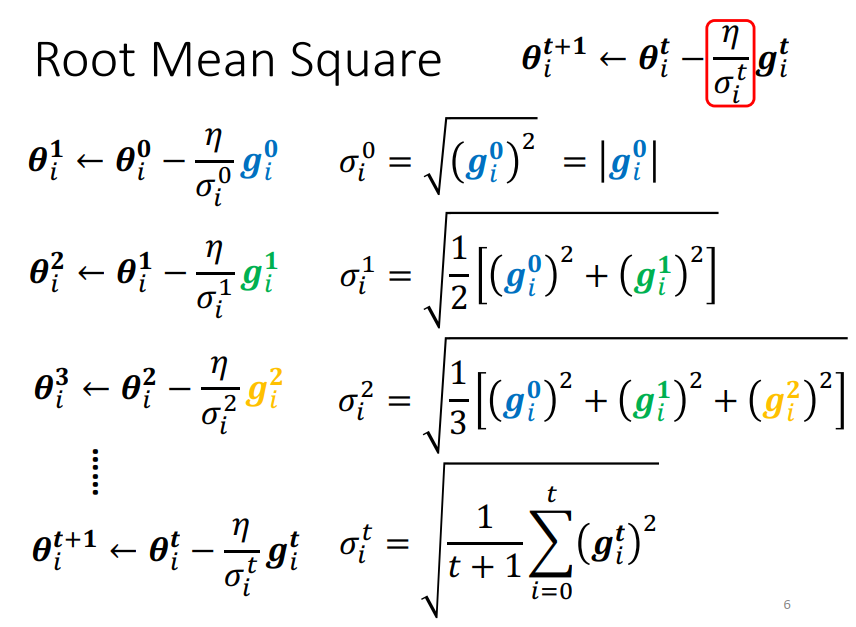
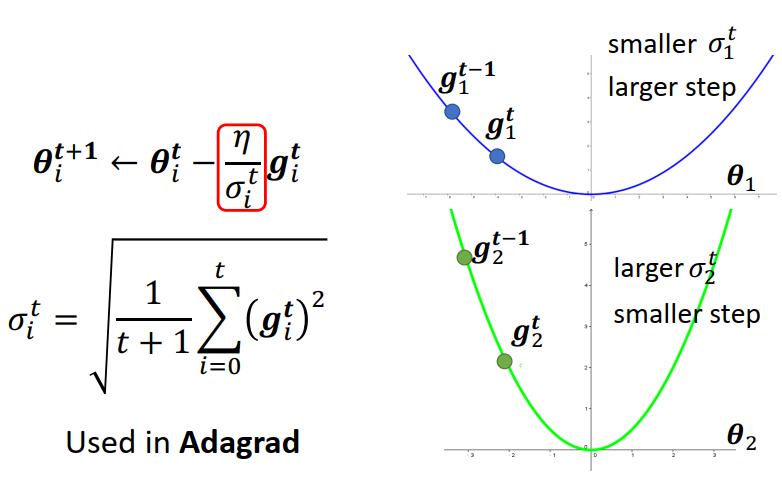
坡度缓的时候,gradient 比较小,而 σ 是gradient的平方和取平均再开根号。
所以 gradient 小 算出来的 σ 就小, σ 小 learning rate 就大。(下图右上角)
坡度陡峭的时候,正好相反,gradient 比较大,σ 就比较大,learning rate 就比较小。(下图右下角)
RMSProp
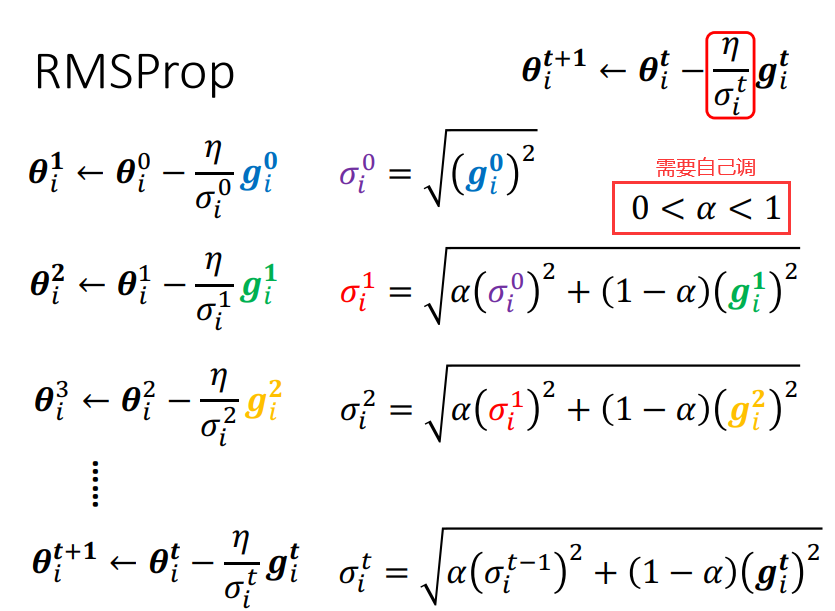
新增的参数 α 是一个hyper parameter,需要自己调它。
以第二步𝜽 i2 ← 𝜽 i1为例:
如果 α 趋于0,就代表说我觉得gi1相较于之前算出的gradient 比较重要;
如果 α 趋于1 ,就代表说我觉得现在算出来的 gi1比较不重要,之前的算出来的gradient比较重要。
由 α 决定 gi1在整个σi1里面占多大的影响力。用 RMSProp 就可以动态调整 σ 这一项。
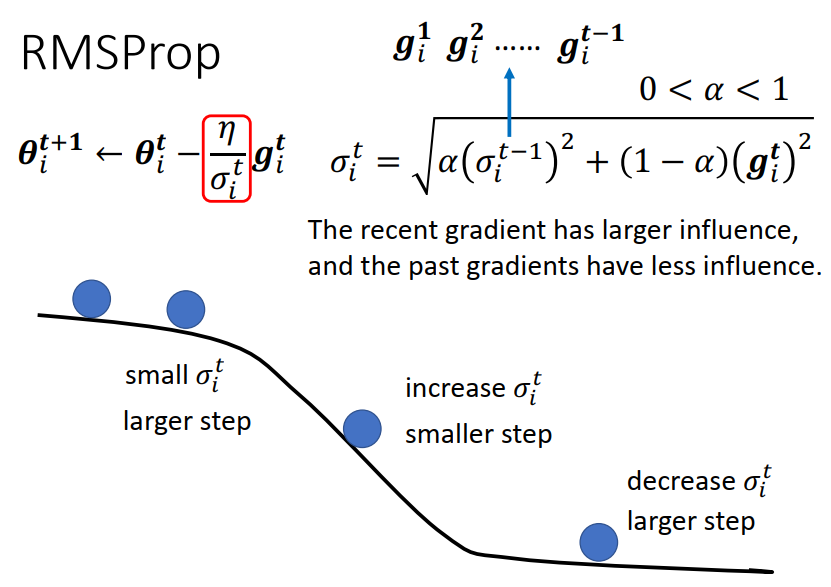
如下:当滚到下坡的时候(第三个点位)gradient 变大,如果用 RMSProp 然后 α 设小一点,就是让刚看到的gradient影响比较大的话,就可以很快的让你的 σ 值变大,也就可以很快的让你的步伐变小(踩一个刹车,避免飞出去)。
Adam:RMSProp + Momentum

在一开始这个简单的 error surface 我们 train不起来,那加上 Adaptive Learning Rate 以后呢?
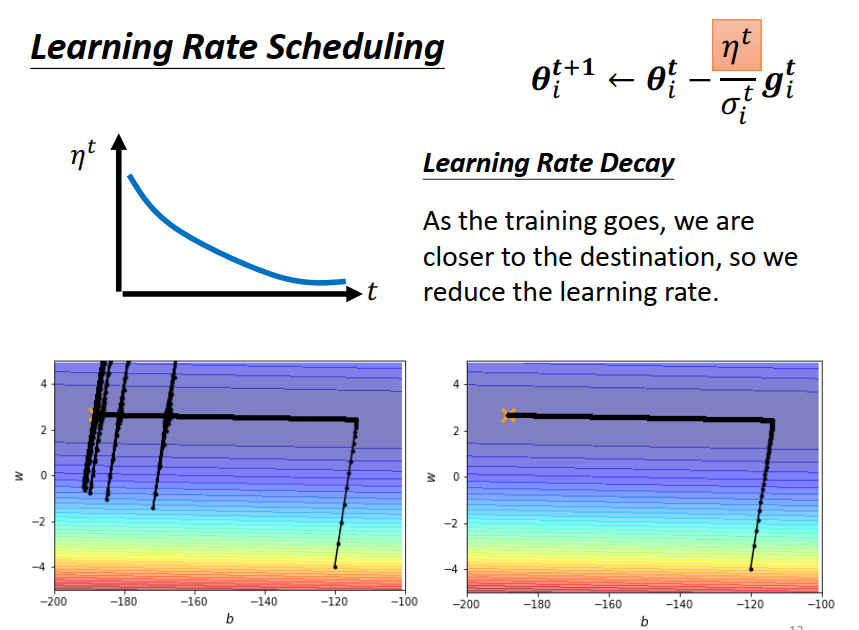
如下图右下角所示,快走到终点的时候发什么一些神奇的事情,因为它是把所有的 gradient 累计,初始的地方很大,后来很小,累计到一定程度后,step(左下红框部分)就变得很大,然后就暴走喷出去了。
喷出去以后没关系,有办法修正回来,因为喷出去以后就走到了gradient比较大的地方, σ 又慢慢变大,步伐就慢慢变小(左右振荡力度变小)又回到中间的峡谷。
解决的暴走的方法:Learning Rate Scheduling
Learning Rate Scheduling:让 η 与时间有关。随着时间增加 让 η 越来越小,因为越更新离终点越近。