[人工智能]【论文复现】ACON Activation（2021）

前言

论文地址：https://arxiv.org/pdf/2009.04759.pdf.

论文源码：https://github.com/nmaac/acon/blob/main/acon.py.

论文贡献：

1. 提出一种新颖的Swish函数解释：Swish函数是ReLU函数的平滑近似（Smoth maximum）。
2. 基于这个发现，论文进一步分析ReLU的一般形式Maxout系列激活函数，再次利用Smoth maximum将Maxout系列扩展得到简单且有效的ACON系列激活函数：ACON-A、ACON-B、ACON-C；
3. 提出meta-ACON，动态的学习（自适应）激活函数的线性/非线性，显著提高了表现。另外还证明了ACON的参数$P_1$和$P_2$负责控制函数的上下限（这个对最终效果由很大的意义）；参数 $\beta$负责动态的控制激活函数的线性/非线性。

一、背景和动机

ReLU激活函数在很长一段时间都是最佳的神经网络激活函数，主要是由于其非饱和、稀疏性等优秀的特性，但是它也同样会产生神经元坏死的严重后果。而近年来人们使用NAS搜索技术找到的Swish激活函数效果非常好，但是问题是Swish激活函数是使用NAS技术暴力搜索出来的，我们无法真正解释Swish激活函数效果这么好的真正原因是什么？在这篇论文中，作者尝试从Swish激活函数和ReLU激活函数的公式出发，挖掘其中的平滑近似原理（Smooth Approximation）。并且将这个原理应用到Maxout family激活函数，提出了一种新型的激活函数：ACON family 激活函数。通过大量实验证明，ACON family 激活函数在分类、检测等任务中性能都优于ReLU和Swish激活函数。

二、相关工作

2.1、激活函数

ReLU


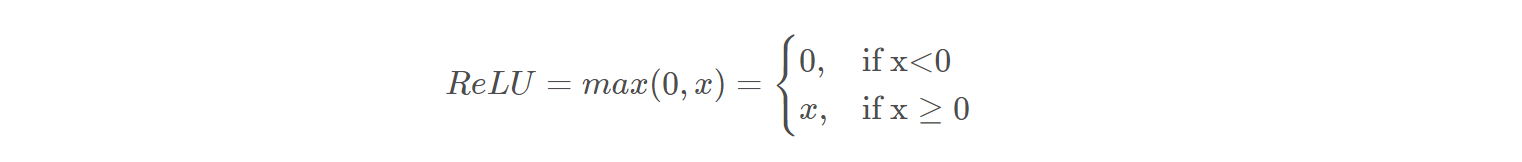
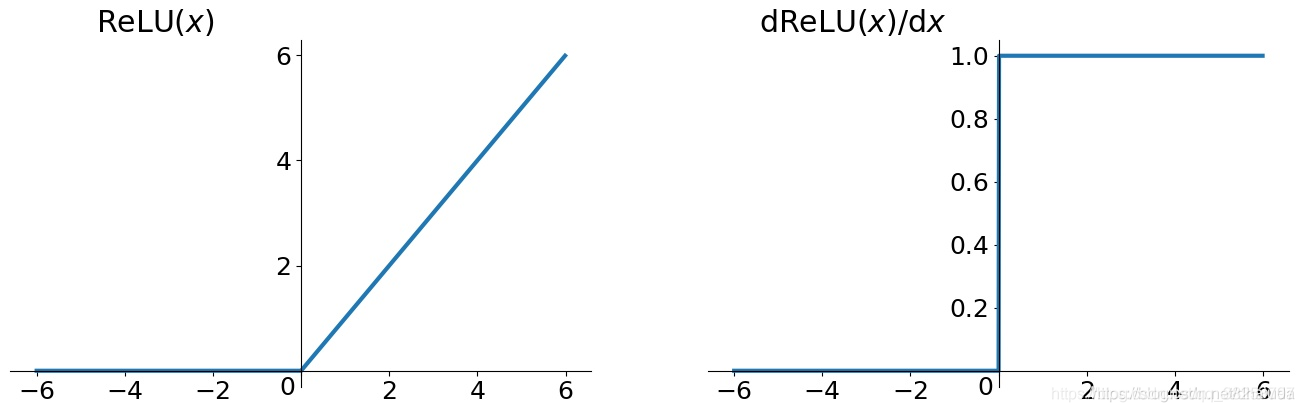
连续 但是在x=0处不可微（non-differentiable）

Maxout
是很多激活函数的通用公式，f(x) = max(a(x), b(x))，常见的如ReLU: f(x) = max(x, 0)，PReLU:f(x) = max(x, px)等。

DY-ReLU
最新的一种激活函数是叫：DY-ReLU (Dynamic ReLU)，是将全局上下文编码为一个超函数，并相应适应 分段线性激活函数（piecewise linear activation），大大增加了参数，但是效果也很好，不过在深度网络的效果没那么显著。

ACON 和 DY-ReLU的区别主要有：

1. ACON学习是否决定激活函数是线性还是非线性
2. ACON参数上比DY-ReLU少很多
3. ACON在深度网络上的效果也很显著，DY-ReLU在深度网络的效果没那么显著。

2.2、动态网络

标准CNNs对所有样本共享相同的网络结构和卷积核，但动态CNNs使用基于输入样本的动态内核、宽度或深度，获得了显著的准确性。以往动态网络的3种形式：

1. 学习动态内核；
2. 使用基于注意力的方法来改变网络结构；
3. 专注于卷积网络的动态深度，对于不同的样本跳过一些层。

而我们提出的ACON Activation 是动态学习选择激活线性还是非线性，动态控制网络的线性和非线性程度。

2.3、神经网络的设计空间

神经网络体系结构的设计主要包括kernel level space和feature level space。最常见的特征设计空间是通过通道维度，空间维度和特征组合来优化性能。在最近流行的核设计空间中，可以优化核形状和核计算。

而本论文提出的是：在非线性水平提供一个新的非线性设计空间 方法是：自适应每一层的非线性程度。

三、ACON

3.1、ReLU -> Swish(Smoth maximum)

先来解释一下什么是Smoth maximum。

上面一段是数学上关于Smoth maximum的定义，它的公式如下所示：

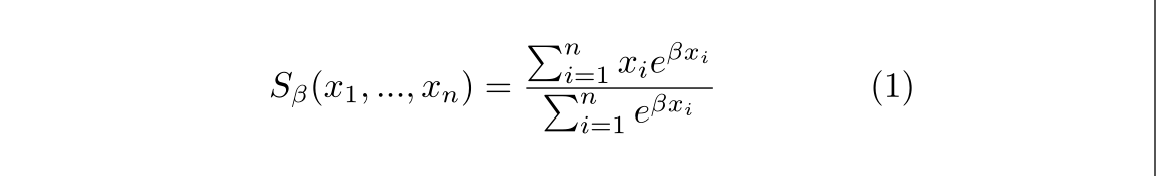
同时它也是 $max(x_1,x_2,\dots \dots ,x_n)$ 函数的平滑近似函数。有以下性质：

1. 当参数$\beta ?>+\infty$ 时，$S_{\beta }?>max(x_1,x_2,\dots ,x_n)$
2. 当参数 $\beta ?>0$ 时，$S_{\beta }=\frac{x_1+x_2+\dots +x_n}{n}$
3. 当参数$\beta ?>?\infty$ 时，$S_{\beta }?>min(x_1,x_2,\dots ,x_n)$

$max(x_1,x_2,\dots \dots ,x_n)$ 函数（Maxout）其实有很多的函数形式，它是一些列类似函数的总和，比如ReLU激活函数就是一个很典型的Maxout函数。我们都很熟悉ReLU：f(x) = max(x, 0)

我们先设 $f(x_1,x_2)=max(x_1,x_2)$，然后利用上面的Smoth maximum公式求它的平滑近似函数有：

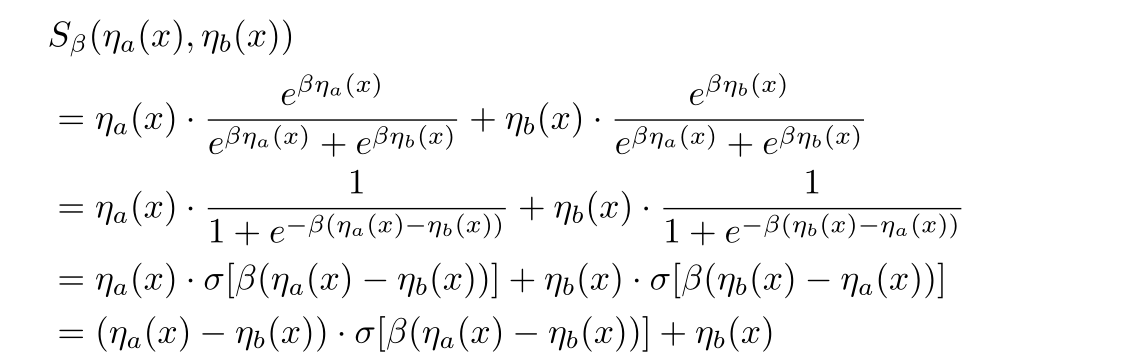
上面是一般形式（论文这里证明的比较复杂，其实直接就可以设两个变量为$x_1$和$x_2$带入计算的），可以看到当 ${\eta }_a(x)=x,{\eta }_b(x)=0$时，$S_{\beta }(x,0)=x?\sigma (\beta x)$，很令人惊讶的结果，这不就是Swish激活函数吗？而且此时 $f(x_1,x_2)=max(x_1,x_2)=max(x,0)=ReLU$

所以我们到这里可以得出结论：ReLU的平滑近似就是Swish。这也给Swish的高效性提供了一个全新的解释。

3.2、Maxout family -> ACON family

利用上面的Smoth maximum的原理和公式，我们可以进一步的通过Maxout family激活函数得到更加高效平滑的ACON family激活函数。

我们这里提出了三个版本的ACON函数：ACON-A、ACON-B、ACON-C.

我们用的比较多的其实是第三个版本ACON-C，它的效果相对是最好的。如下图a是ACON-C的函数图像随 $p_1$ 和 $p_2$变化的情况（p1和p2使用的是两个可学习参数来自适应调整）：

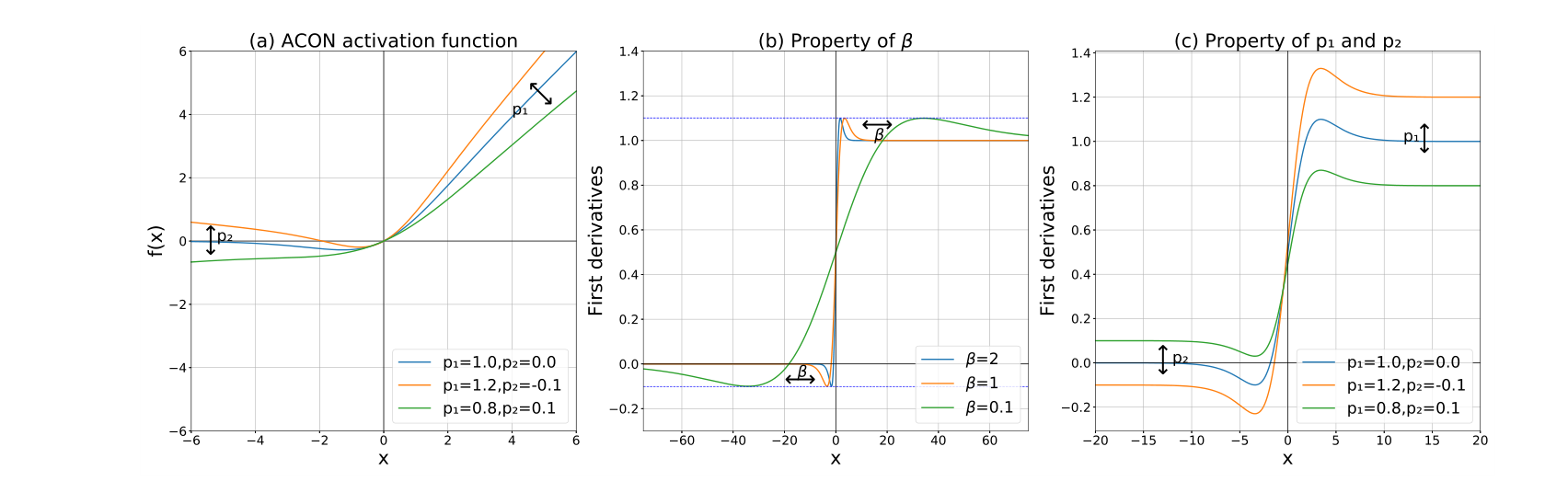
我们简单看下ACON-C的函数性质

由上图c可以看出ACON-C的一阶导数上下界会根据p1和p2的变化而浮动。现在我们用数学公式来看下是怎么回事。
对其求一阶导：

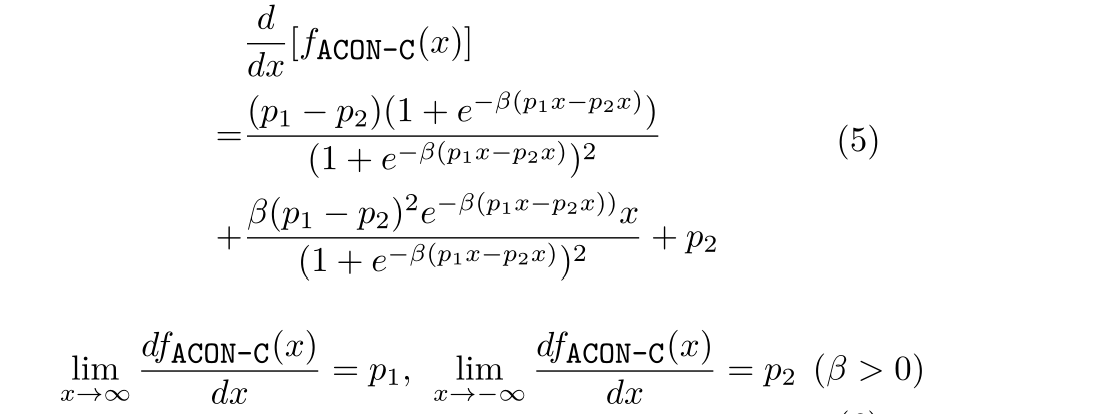
可以看到当 $x?>+\infty$一阶导数 $?>p_1$；当 $x?>?\infty$一阶导数 $?>p_2$
再对其求二阶导：

为了求出一阶导的上下限，我们令二阶导为0，求出：

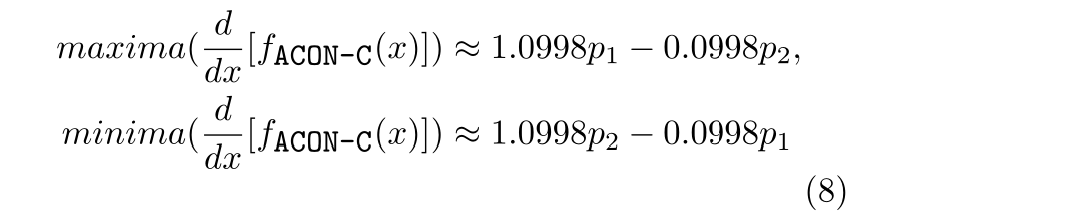
可以看到ACON-C的一阶导数的上下界也是通过p1和p2两个参数来共同决定的。
这两个性质对最终结果是至关重要的，我们可以通过学习$P1$和$P2$，使用性能更好的激活函数。

3.3、Meta-ACON

细心的朋友肯定会发现，说了这么多，前面我们说到ACON激活函数还由一个很重要的特点：自适应控制激活函数是线性还是非线性，还没说呢。下面我们来聊一聊。

还是从更普遍版本的ACON-C说起，上面说了它的 $p_1$和 $p_2$两个参数的作用，还要有一个超参 $\beta$的作用没有说。我们从上面的公式知道，超参 $\beta$控制着 Smoth maximum 平滑函数的类型。如下所示：

1. 当参数$\beta ?>+\infty$ 时，$S_{\beta }?>max(x_1,x_2,\dots ,x_n)$
2. 当参数 $\beta ?>0$ 时，$S_{\beta }=\frac{x_1+x_2+\dots +x_n}{n}$
3. 当参数$\beta ?>?\infty$ 时，$S_{\beta }?>min(x_1,x_2,\dots ,x_n)$

可以看出，当$\beta ?>+\infty$ 时函数是非线性的，当参数 $\beta ?>0$ 时，是函数线性的。因此可以得出结论：参数$\beta$ 控制着激活函数是线性还是非线性。这点从下图可以直观的看出来：

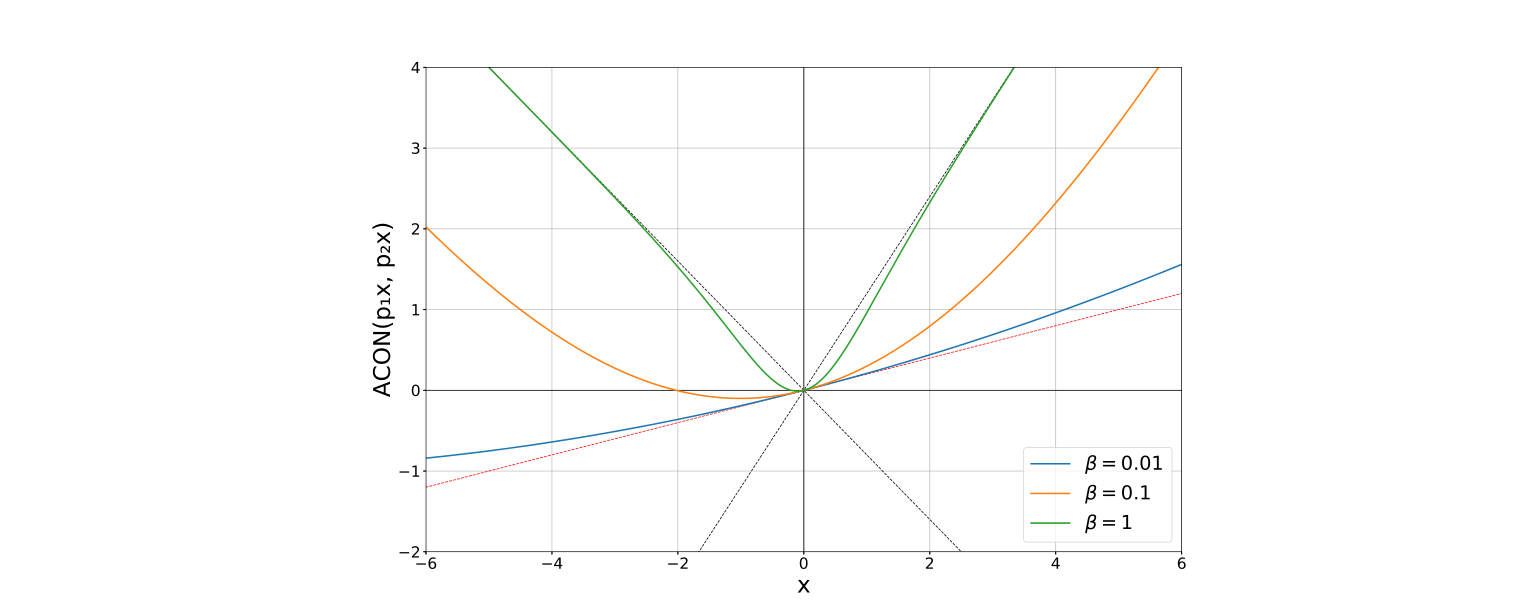
因此，与ReLU等传统激活不同，ACON允许每个神经元自适应激活或不激活如下图：

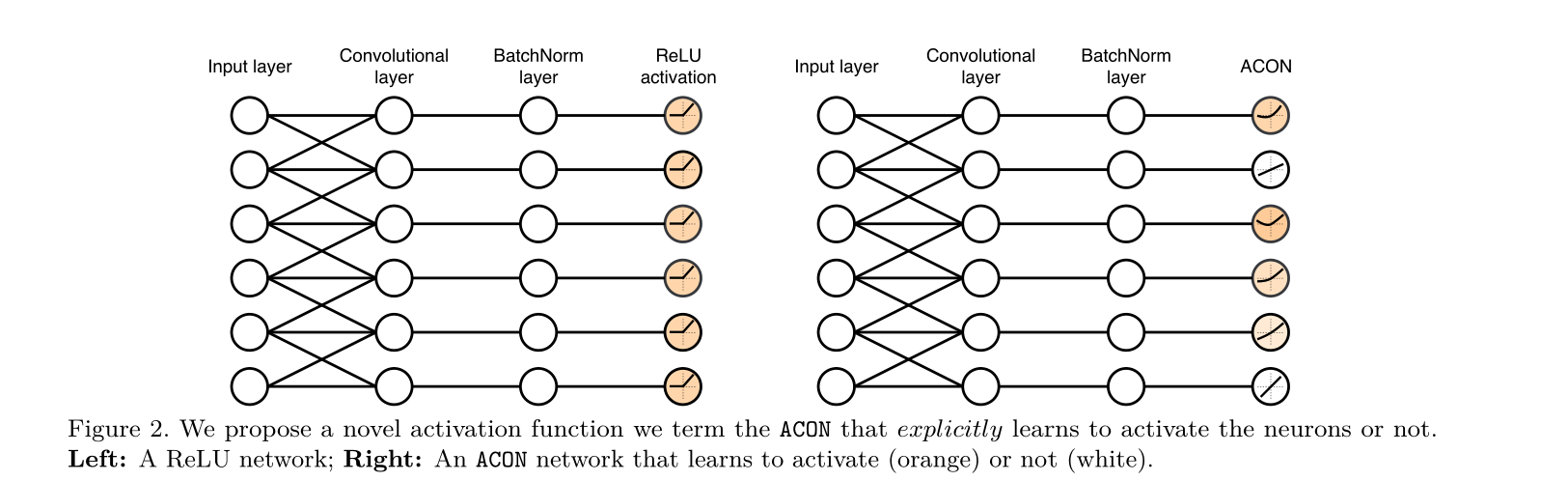
假如这个$\beta$是常量，那么ACON-C激活函数的线性非线性能力也就定了，我们当然不希望这样，所以我们提出一个G(x)模块来由输入特征图x（CxHxW）来动态的学习β，以达到动态的（自适应）控制函数线性/非线性能力（这种定制的激活行为有助于提高泛化和传递性能。）。

而自适应函数的设计空间包含了layer-wise，channel-wise，pixel-wise这三种空间，分别对应的是层，通道，像素。如下所示：

这里我们选择了channel-wise，首先分别对H, W维度求均值，然后通过两个卷积层，使得每一个通道所有像素共享一个权重， 最后由sigmoid激活函数求得β。为了减少参数我们在两个中间的channel加了个缩放参数r，我们设置为16。

四、论文实验结果

分类任务

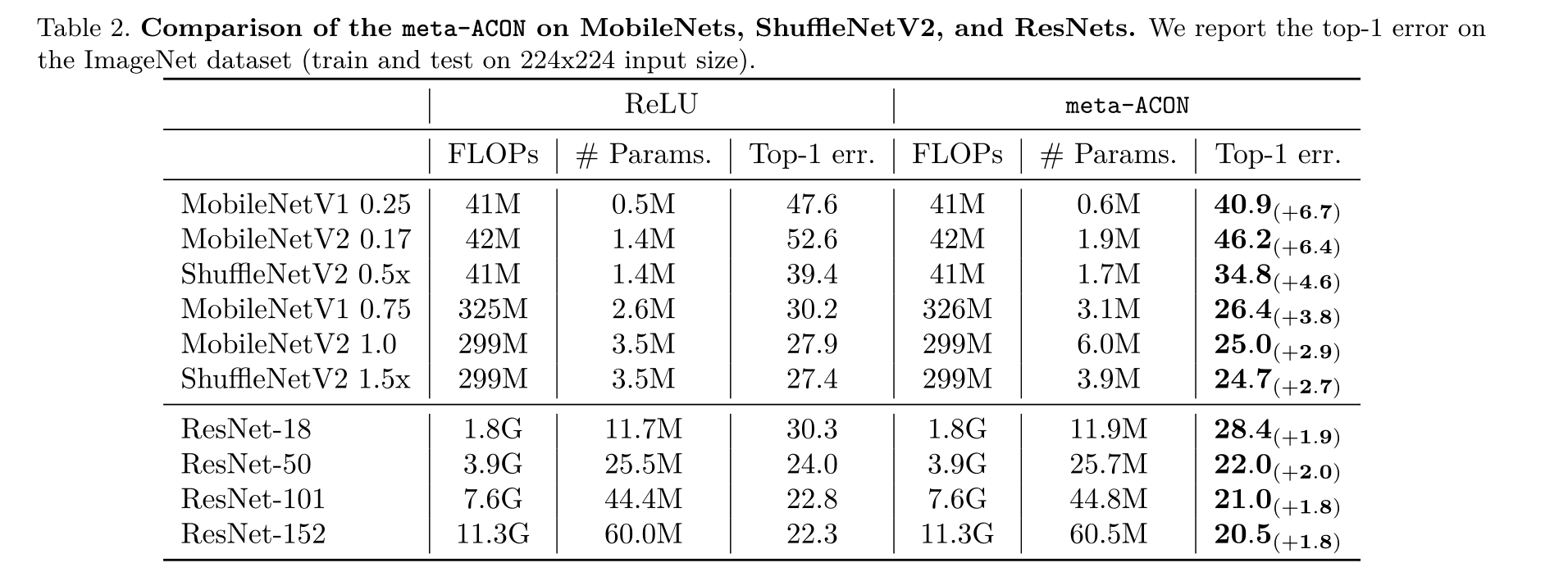
从上图可以看出，在MobileNet、ShuffleNetV2 and ResNets 等分类网络上，meta-ACON的FLOPs和Params和ReLU相当，但是却可以大大降低Top1的error.

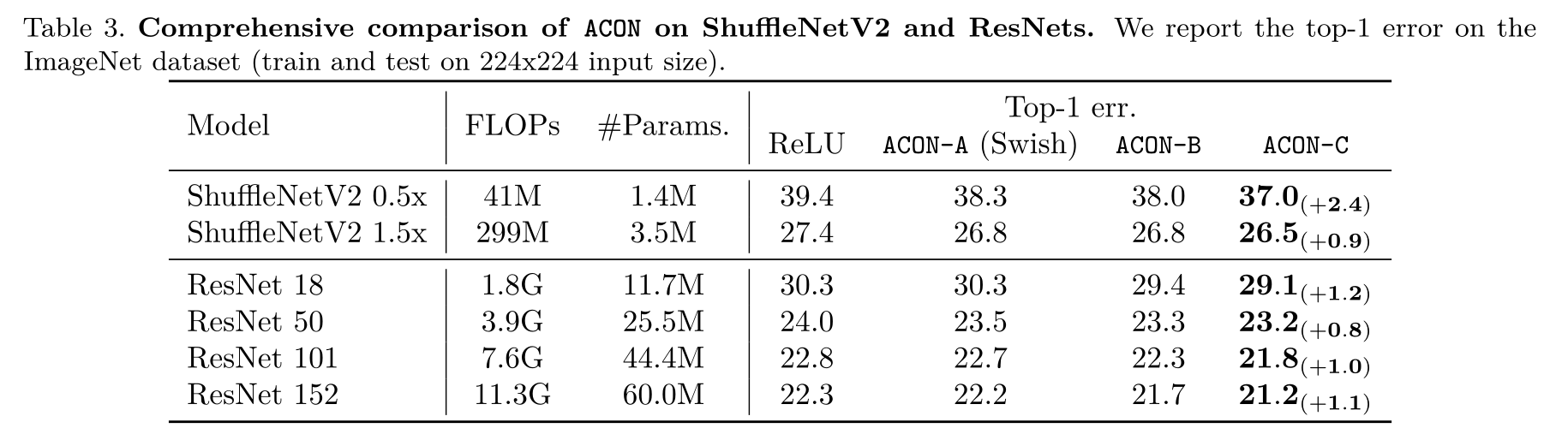
从上图可以看出，ACON family在ShuffleNetV2和ResNets网络上的表现，发现ACON family的Top1分类误差都要低于ReLU，且ACON-C的最优。

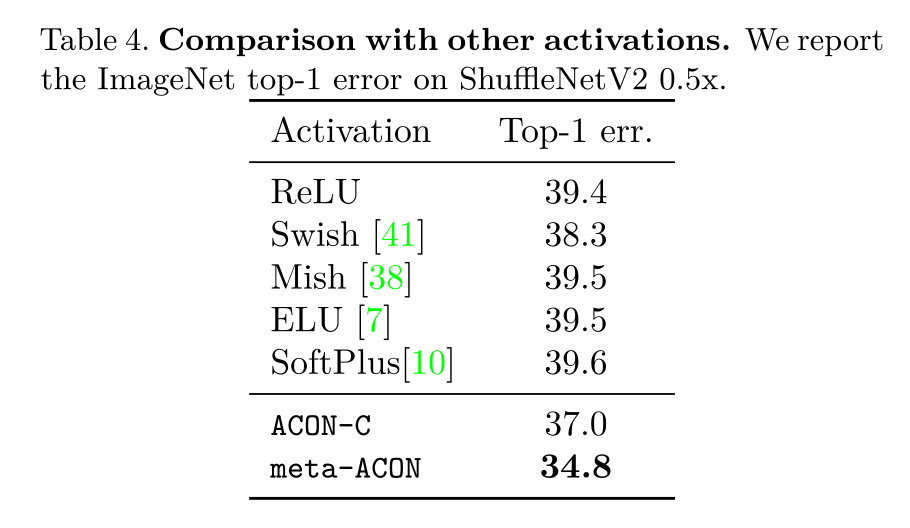
从上图可以看出，和其他种类的激活函数相比，也是ACON-C和meta-ACON的表现更好，且meta-ACON性能远远优于ACON-C。

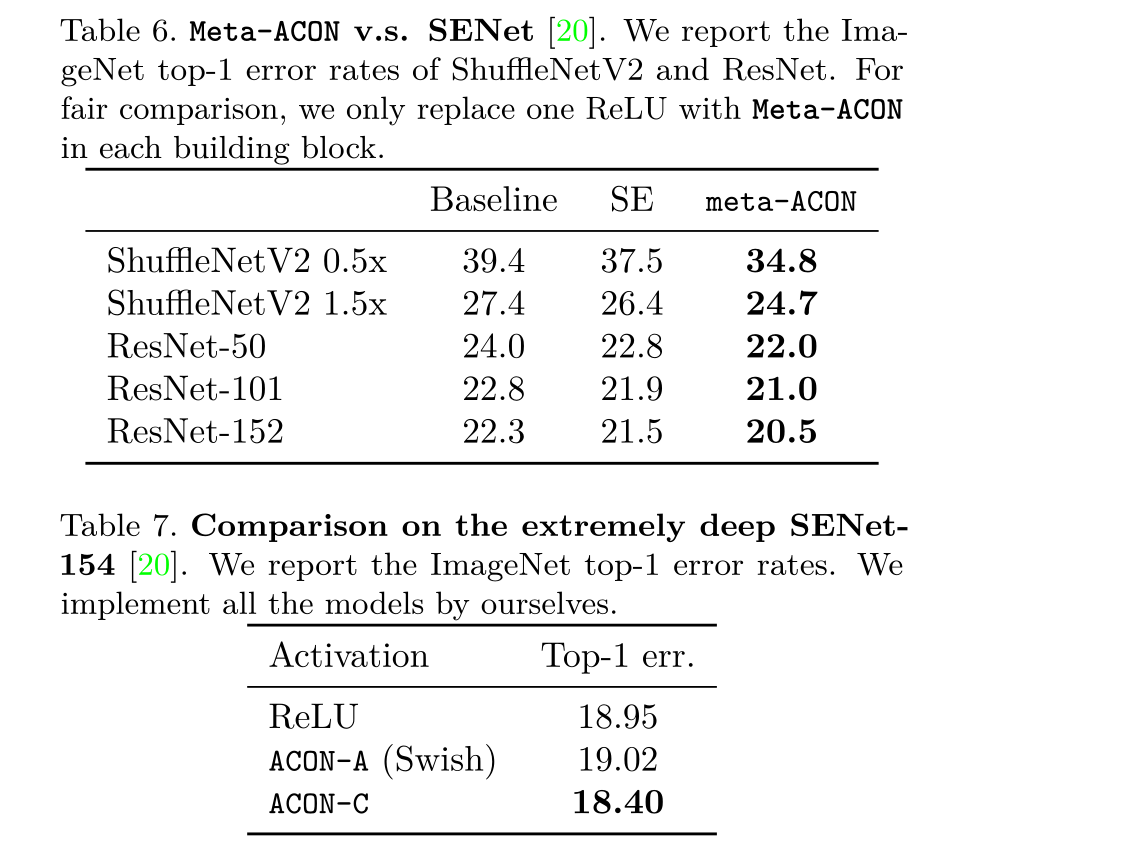
而且meta-ACON和ACON-C的性能即便在更深的网络中依然表现的很稳定如上图

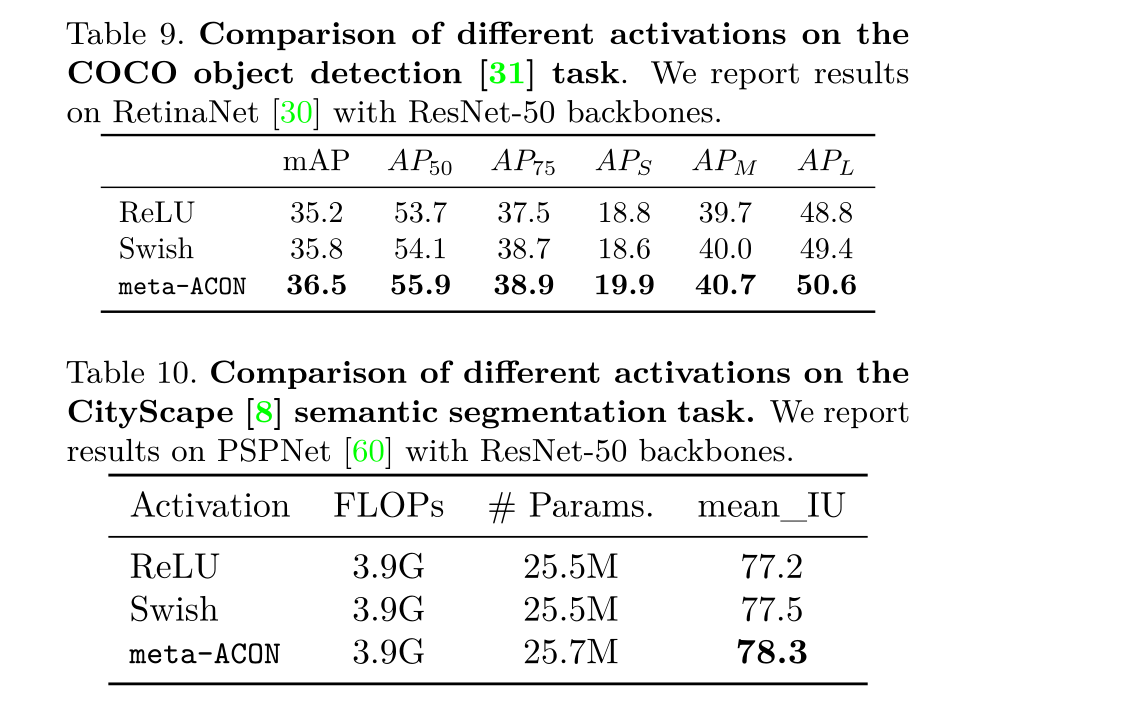
如上图，进一步将meta-ACON激活函数推广（generalization）到目标检测领域，meta-ACON依然有着很不错的性能（优于ReLU和Swish），且参数量Params和FLOPs也几乎没什么增加。

总结：meta-ACON激活函数无论在分类（甚至是很深的网络）和目标检测领域的性能都要优于ReLU和Swish（且参数量和FLOPs几乎一样的情况下）。ACON-C的性能要差meta-ACON一点，但也很不错。

五、PyTorch实现

ACON-C:

class AconC(nn.Module):
    """
    ACON activation (Activate or Not: Learning Customized Activation).
    ACON https://arxiv.org/pdf/2009.04759.pdf
    AconC: (p1*x-p2*x) * sigmoid(beta*(p1*x-p2*x)) + p2*x, beta is a learnable parameter
    """
    def __init__(self, c1):  # ch_in
        super().__init__()
        # p1、p2 and beta are channel-wise
        self.p1 = nn.Parameter(torch.randn(1, c1, 1, 1))
        self.p2 = nn.Parameter(torch.randn(1, c1, 1, 1))
        self.beta = nn.Parameter(torch.ones(1, c1, 1, 1))

    def forward(self, x):
        dpx = (self.p1 - self.p2) * x
        return dpx * torch.sigmoid(self.beta * dpx) + self.p2 * x

meta-ACON:

class MetaAconC(nn.Module):
    """ ACON activation (activate or not).
    MetaAconC: (p1*x-p2*x) * sigmoid(beta*(p1*x-p2*x)) + p2*x, beta is generated by a small network
    """
    def __init__(self, c1, k=1, s=1, r=16):  # ch_in, kernel, stride, r
        super().__init__()
        c2 = max(r, c1 // r)  # 为了减少参数我们在两个中间的channel加了个缩放参数r，我们设置为16。
        self.p1 = nn.Parameter(torch.randn(1, c1, 1, 1))
        self.p2 = nn.Parameter(torch.randn(1, c1, 1, 1))
        self.fc1 = nn.Conv2d(c1, c2, k, s, bias=True)
        self.fc2 = nn.Conv2d(c2, c1, k, s, bias=True)
        # self.bn1 = nn.BatchNorm2d(c2)
        # self.bn2 = nn.BatchNorm2d(c1)

    def forward(self, x):  # x [bs, c, w, h]
        # 1、分别对H, W维度求均值
        y = x.mean(dim=2, keepdims=True).mean(dim=3, keepdims=True)
        # batch-size 1 bug/instabilities https://github.com/ultralytics/yolov5/issues/2891
        # beta = torch.sigmoid(self.bn2(self.fc2(self.bn1(self.fc1(y)))))  # bug/unstable
        # 然后通过两个卷积层, 使得每一个通道所有像素共享一个权重 最后由sigmoid激活函数求得可学习参数β
        beta = torch.sigmoid(self.fc2(self.fc1(y)))  # bug patch BN layers removed
        # 最后带入公式
        dpx = (self.p1 - self.p2) * x
        return dpx * torch.sigmoid(beta * dpx) + self.p2 * x

Reference

链接: 博客1.
链接: 知乎1.
链接: https://en.wikipedia.org/wiki/Smooth_maximum.