[人工智能]主流的深度学习优化方法（SGD，SGDM，Adagrad，RMSProp，Adam）

0 前言

介绍主流的深度学习优化方法（SGD，SGD with Momentum，Adagrad，RMSProp，Adam），梯度优化的基本原则是起始的时候降得快，后来降的慢，以此原则来理解下面这些算法。理解不是非常深，有问题希望大家指出。

1 SGD

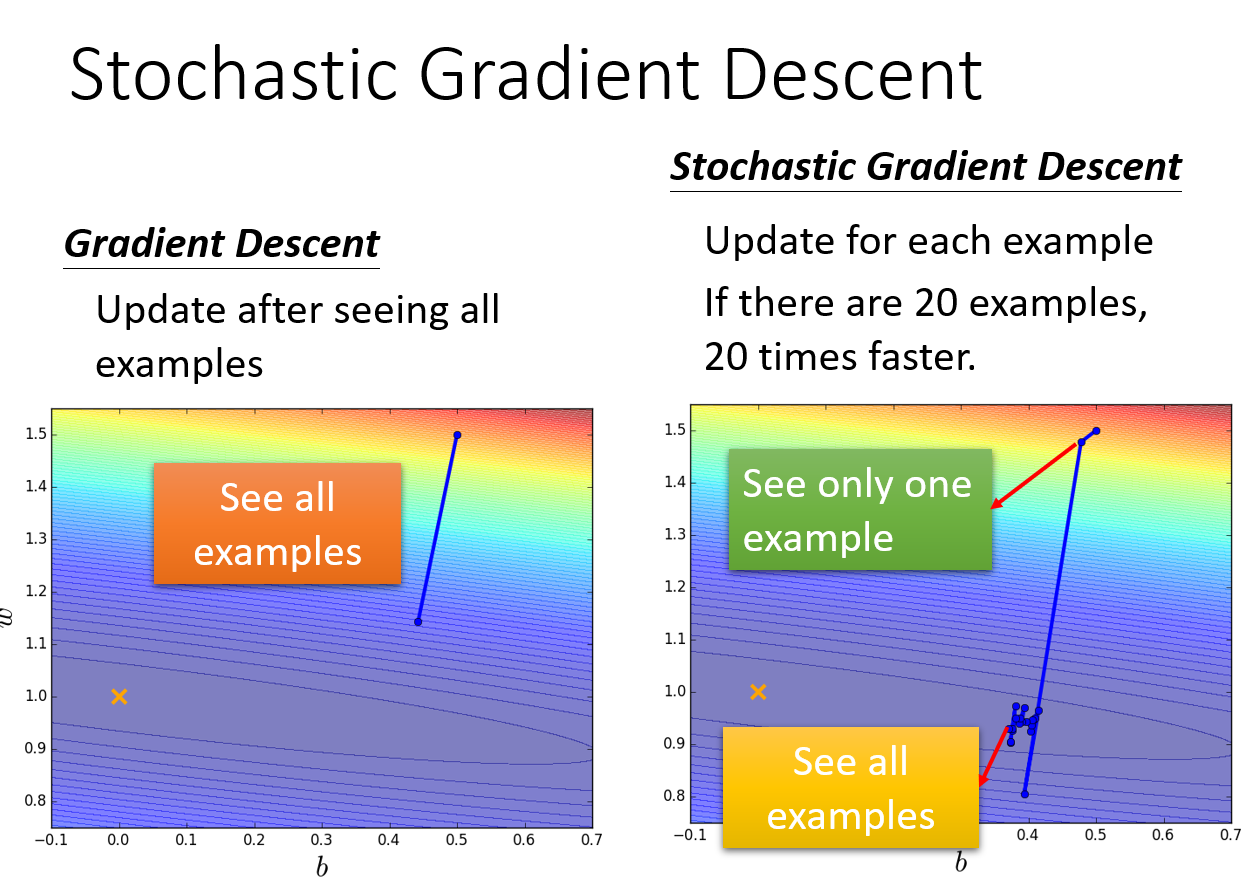
一般的梯度下降所用的损失函数会计算所有样本的损失，但是随机梯度下降比梯度下降多了随机两个字，也即用样本中的一个例子的损失值来代替整体的损失。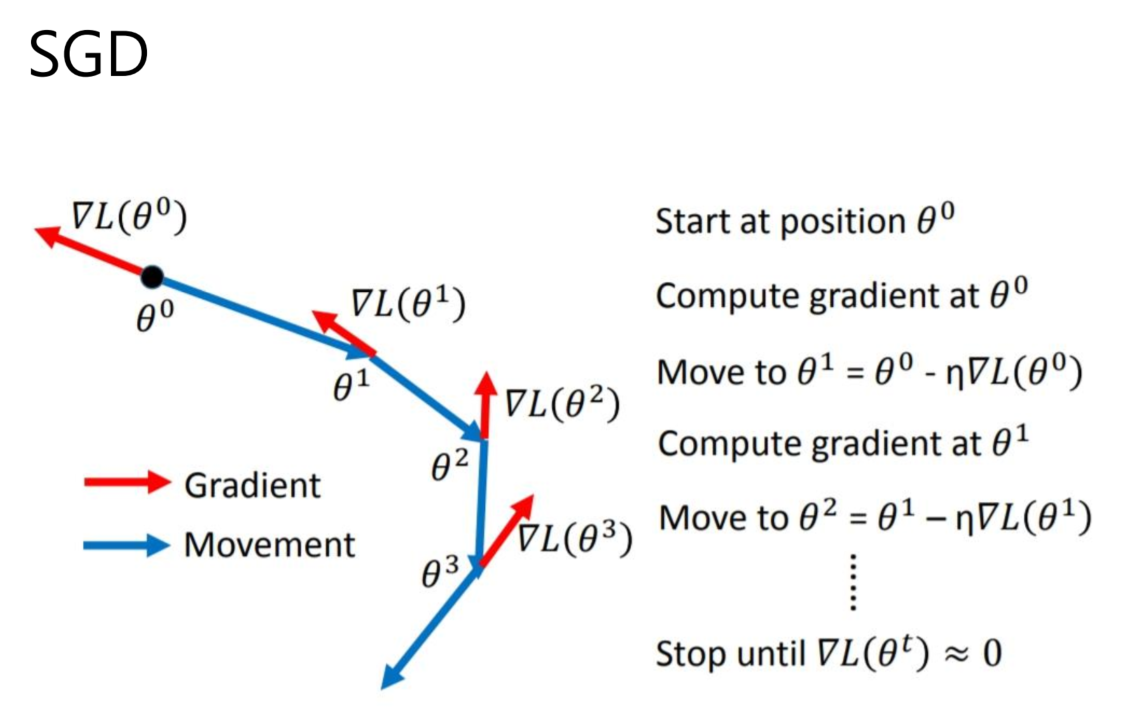
因而随机梯度下降是会带来一定的问题，因为计算得到的并不是准确的一个梯度。如下图，SGD是按照单个样本更新，所以前面几次更新时很难保证沿着梯度下降，但是随着样本数增多，后面会接近最低点，相同计算量的前提下比GD效果好。

2 SGD with momentum（SGDM）

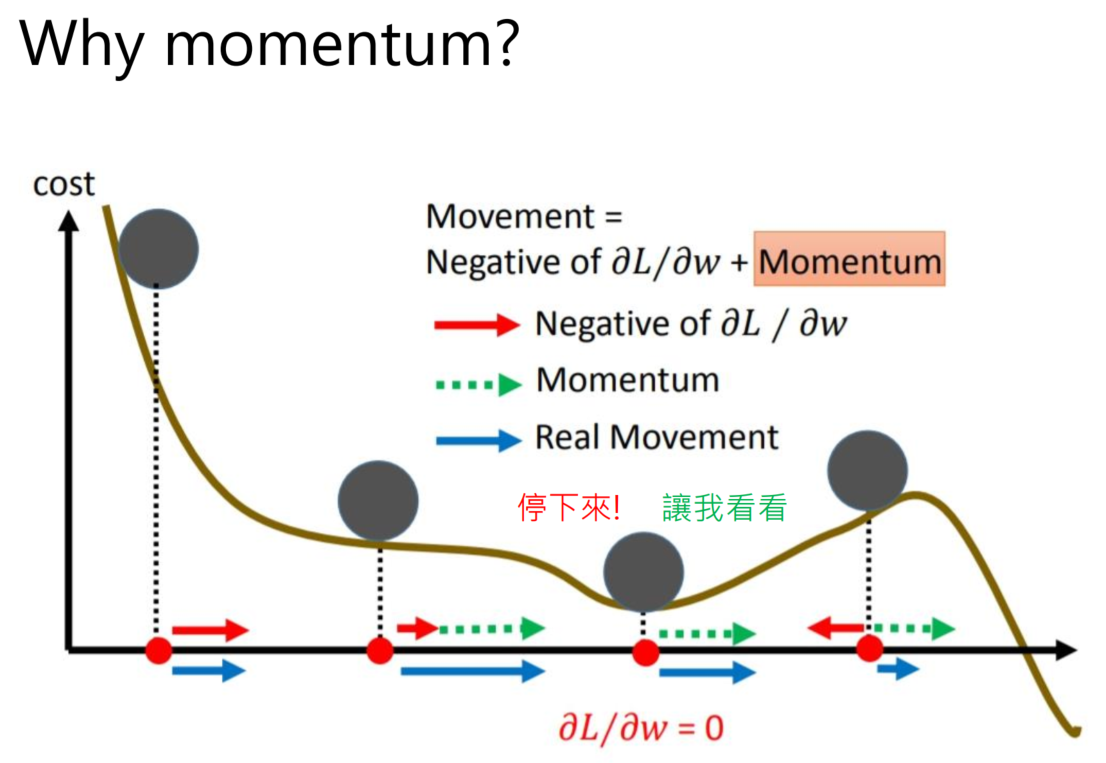
SGDM也就是SGD+ Momentum，这里引入了一阶动量。从直观理解就是加入了一个惯性，在坡度比较陡的地方，会有较大的惯性，这是下降的多。坡度平缓的地方，惯性较小，下降的会比较慢。

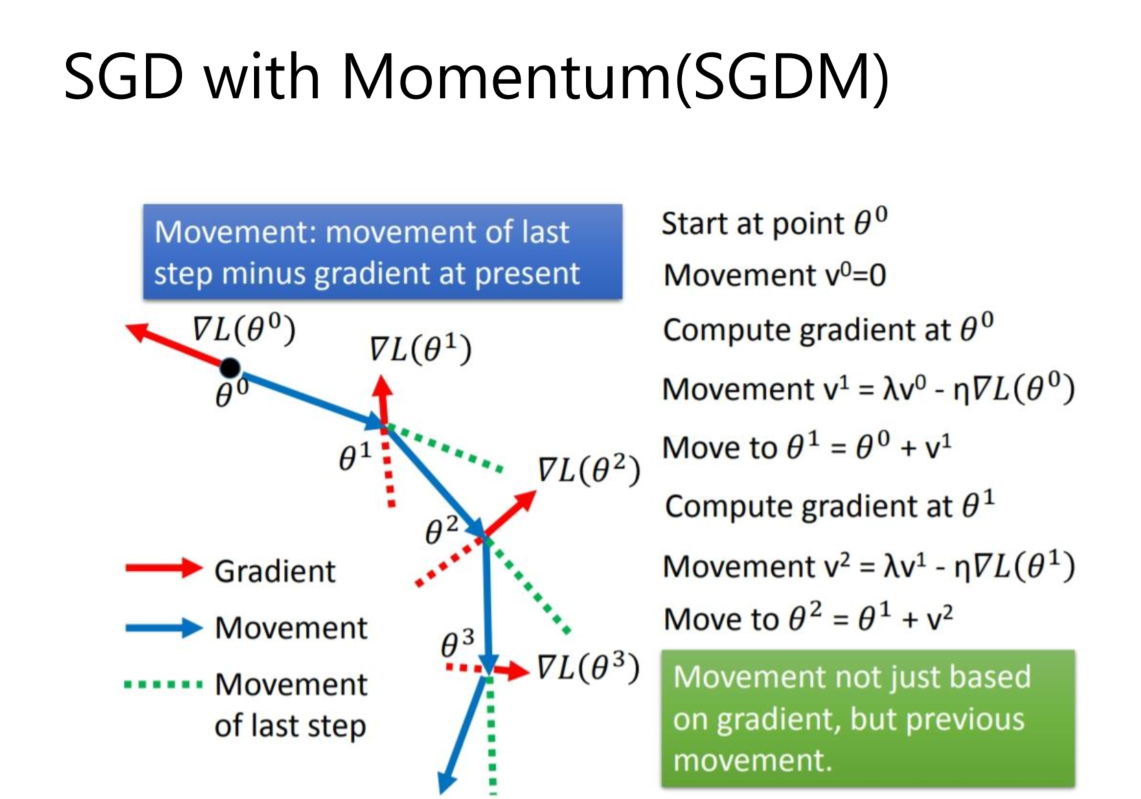
V是前面梯度值的和。

之前的梯度大小会影响下一次的梯度下降：

3 Adagrad

起到的效果是在参数空间更为平缓的方向，会取得更大的进步（因为平缓，所以历史梯度平方和较小，对应学习下降的幅度较小），并且能够使得陡峭的方向变得平缓，从而加快训练速度。

其中：


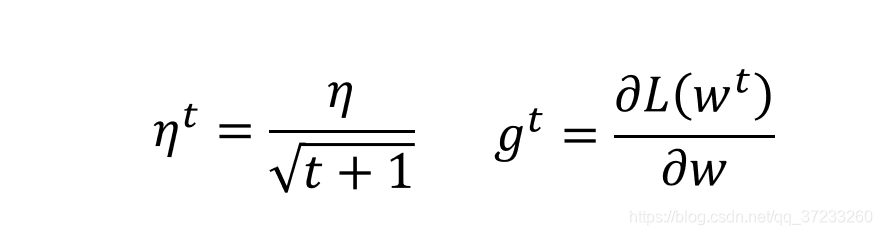
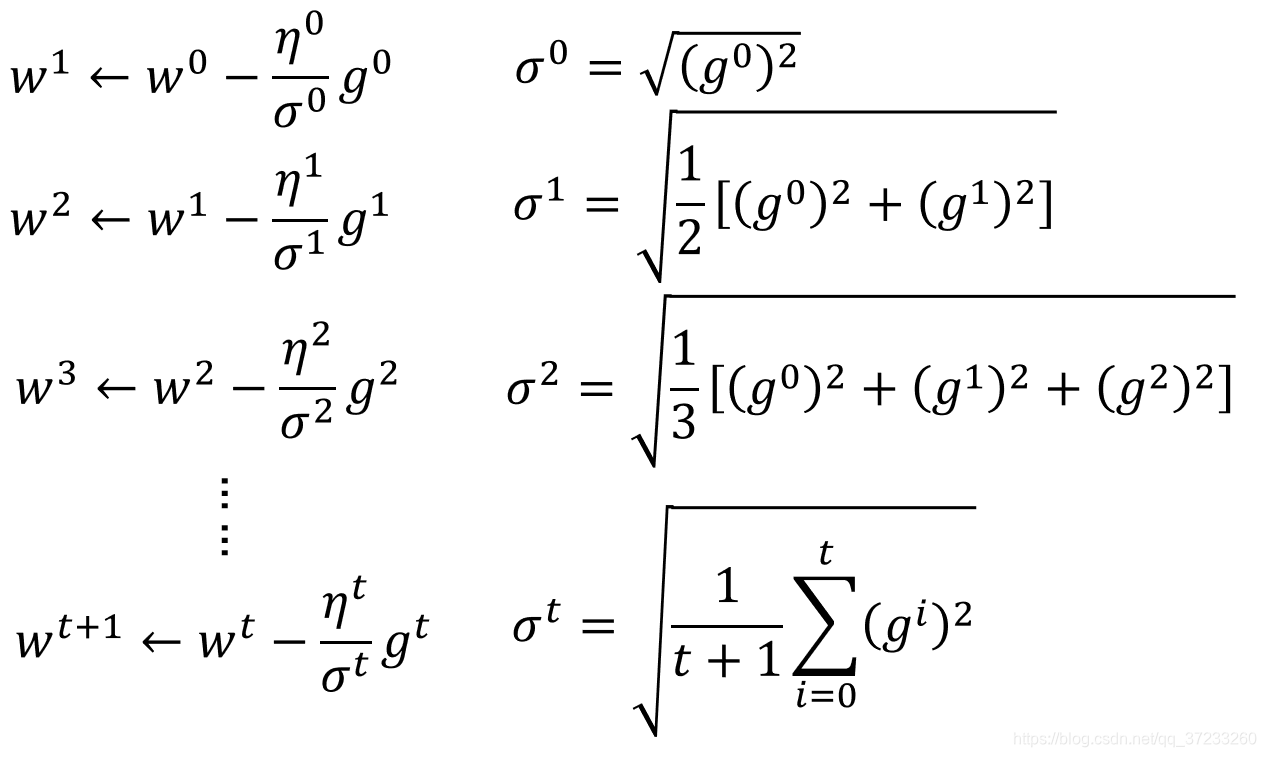
代入消元可得最终表达式：

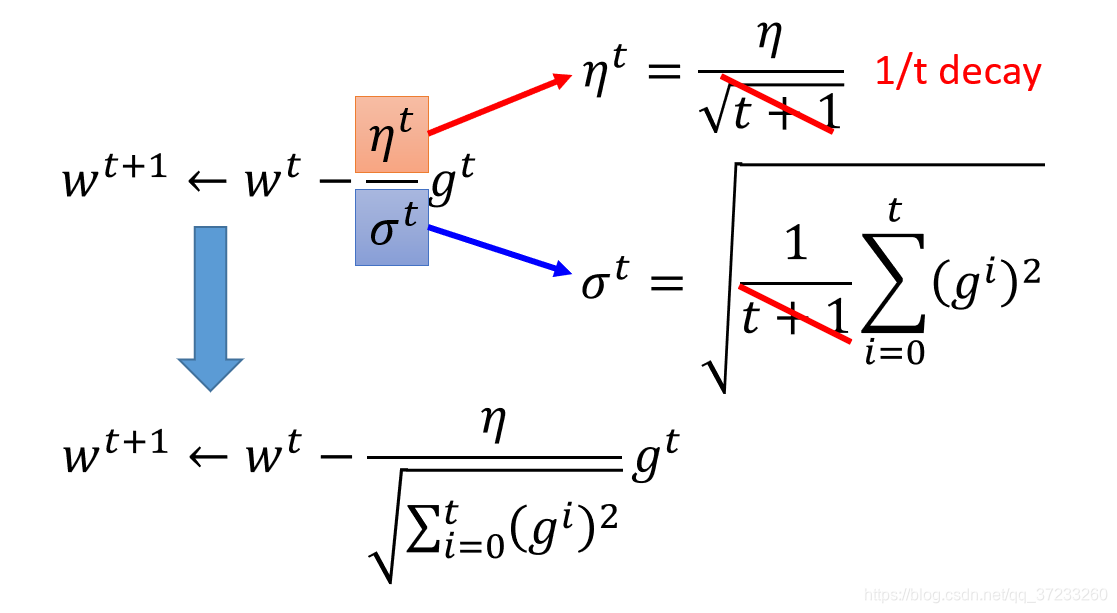
分母为累计平方梯度，且η为超参数，那么在每一轮迭代中学习率会越来越小，也就是说当前位置的梯度对参数的影响也越来越小。AdaGrad 算法在初始时鼓励收敛，随着迭代的深入慢慢变成惩罚收敛，速度也越来越慢。

4 RMSProp（root mean square prop）

因为Adagrad算法会出现提前停止的现象，所以在RMSProp（均方根传递）算法中解决了这个问题，RMSProp优化算法和AdaGrad算法唯一的不同，就在于累积平方梯度的求法不同。RMSProp算法不是像AdaGrad算法那样暴力直接的累加平方梯度，而是加了一个衰减系数来控制历史信息的获取多少，一般取0.9或者0.5，它采用指数加权平均的思想，只将最近的梯度进行累加计算平方。见下：

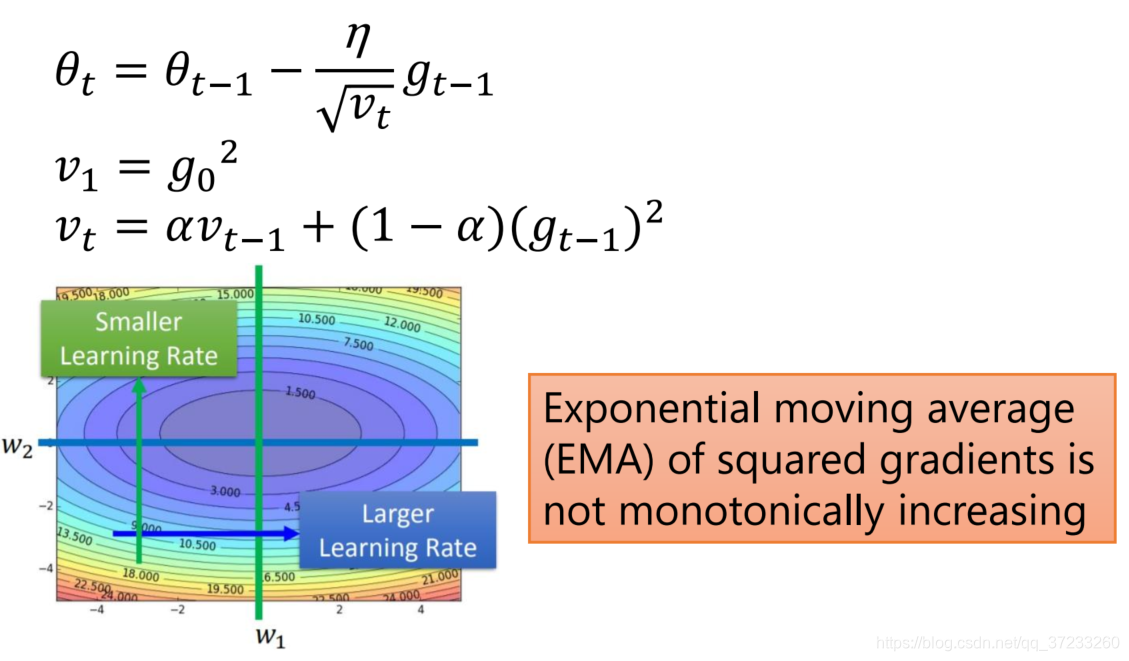
仍然是累加平方梯度，只是离的越远的梯度的权值越小，离的越近的越大，因为展开之后初始的梯度之前有很多累乘的系数。

5 Adam

虽然SGDM加速了我们对最小值方向的搜索，但RMSProp阻碍了我们在振荡方向上的搜索。Adam通过名字我们就可以看出他是基于SGDM和RMSProp的微调版本，该方法是目前深度学习中最流行的优化方法，在默认情况尽量使用Adam作为参数的更新方式。

和SGDM一样计算，加入动量，计算衰减梯度：
$$m_t={\beta }_1?m_{t?1}+\left(1?{\beta }_1\right)g_{t?1}$$
和RMSProp算法类似，计算衰减学习率：
$$v_t={\beta }_2?v_{t?1}+\left(1?{\beta }_2\right){\left(g_{t?1}\right)}^2$$
最后更新参数：
$${\theta }_t={\theta }_{t?1}?\frac{\eta }{\sqrt{{\hat{v}}_t}+\epsilon }{\hat{m}}_t$$