机器学习的相关BP算法理解
一.BP算法
1.什么是BP算法
BP算法由信号的正向传播和误差的反向传播两个过程组成
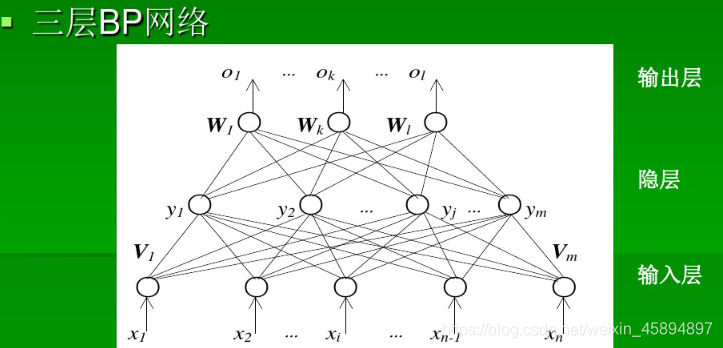
正向传播 时,输入样本从输入层进入网络,经过隐层逐层传递至输出层,如果输出层实际输出与期望输出不同,则误差反向传播;如果相同,则结束算法。
反向传播 时,输出误差按照原路返回计算,先到隐层,再到输入层。反传过程中将误差分给各层各个单元,获得各层各单元的误差信号,并将其作为修正各单元权值的依据。通过梯度下降法不断调整各层神经元的权值,使误差信号减小到最低限度。
2.BP算法的简要步骤
(1)初始化,用小的随机数给各个权值赋初值。
(2)读取参数和训练样本集
(3)归一化处理
(4)对训练集中每一个样本进行计算
(5)满足要求或者条件的结束训练,否则的话,转入步骤4继续。
二.“挑选西瓜”的核心算法
1.preprocess函数:将文字转化为数字,LabelEncoder只适用于转化一列文本数据,转换多列需要factorize方法
2.尝试代码为X=StandardScaler.fit_transform(X),并去掉前面的ss=StandardScaler()报错,因为涉及了两个类,需要先对类实例化,即a=A()
计算基于数学函数方法,如果用文字不能处理,使用LavelEncoder方法转换为数字
#定义Sigmoid
def sigmoid(x):
x=np.array(x,dtype=np.float64)
return 1/(1+np.exp(-x))
#求导
def d_sigmoid(x):
return x*(1-x)
def preprocess(data):
for title in data.columns:
if data[title].dtype=='object':
#print(data[title])
#print("#######")
#每列相同类别转化为同一个数字,不同类别之间不同数字
encoder = LabelEncoder()
data[title] = encoder.fit_transform(data[title])
#print(data[title])
#print("############")
ss = StandardScaler()
#去掉“好瓜”这一列
X = data.drop('好瓜',axis=1)
#print(X)
Y = data['好瓜']
#print(Y)
#StndardScaler.fit_transform计算数据均值和方差,并把数据转换成标准的正态分布
#17行数据17个列表
X = ss.fit_transform(X)
#print(X)
#print(Y)
#将“好瓜”这一列转化为数字的数据reshape为一行
x,y = np.array(X),np.array(Y).reshape(Y.shape[0],1)
#print(x)
#print(y)
return x,y
def accumulate_BP(x,y,dim=10,eta=0.8,max_iter=500):
n_samples = x.shape[0]
w1 = [[random.random() for i in range(dim)] for j in range(x.shape[1])]
b1 = [random.random() for i in range(dim)]
w2 = [[random.random() for i in range(1)] for j in range(dim)]
b2 = [random.random() for i in range(1)]
losslist = []
for ite in range(max_iter):
##前向传播
#点积 A[0]B[0]+A[1]B[1]+...+A[n]B[n]
u1 = np.dot(x,w1)-b1
out1 = sigmoid(u1)
u2 = np.dot(out1,w2)-b2
out2 = sigmoid(u2)
loss = np.mean(np.square(y - out2))/2
losslist.append(loss)
print('iter:%d loss:%.4f'%(ite,loss))
#补充反向传播代码
g=out2*(1-out2)*(y-out2) #书上式(5.10)
e=out1*(1-out1)*((np.dot(w2, g.T)).T)#书上式(5.15)
d_w1=-np.dot(x.T,e)#书上式(5.13)
d_w2=-np.dot(out1.T,g)#书上式(5.11)
d_b1=e#书上式(5.14)
d_b2=g#书上式(5.12)
##更新
w1 = w1 - eta*d_w1
w2 = w2 - eta*d_w2
b1 = b1 - eta*d_b1
b2 = b2 - eta*d_b2
plt.figure()
##Loss可视化代码
plt.plot(losslist)
plt.show()
return w1,w2,b1,b2
def standard_BP(x,y,dim=10,eta=0.8,max_iter=500):
n_samples = 1
w1 = [[random.random() for i in range(dim)] for j in range(x.shape[1])]
b1 = [random.random() for i in range(dim)]
w2 = [[random.random() for i in range(1)] for j in range(dim)]
b2 = [random.random() for i in range(1)]
losslist = []
#标准BP算法代码
for i in range(max_iter):
for j in range(x.shape[0]):#标准BP算法针对每一个样例
alpha=np.dot(x[j],w1)#隐层神经元的输入
b=sigmoid(alpha-b1)#隐层的输出
beta=np.dot(b,w2)#输出神经元的输入
predictY=sigmoid(beta-b2)#预测值
E=sum(((predictY-y[j])**2)/2)#损失值
print(E)
losslist.append(E)
g=predictY*(1-predictY)*(y[j]-predictY)#书上式(5.10)
e=b*(1-b)*((np.dot(w2,g.T)).T)#书上式(5.15)
w2+=eta*np.dot(b.reshape((dim,1)),g.reshape((1,1)))#书上式(5.11)
b2-=eta*g#书上式(5.12)
w1+=eta*np.dot(x[j].reshape((x.shape[1],1)),e.reshape((1,dim)))#书上式(5.13)
b1-=eta*e#书上式(5.14)
#Loss可视化代码
plt.plot(losslist)
plt.show()
return w1,w2,b1,b2
data = pd.read_table('./testdata/watermelon30.txt',delimiter=',')
data.drop('编号',axis=1,inplace=True)
x,y = preprocess(data)
dim = 10
w1,w2,b1,b2 = accumulate_BP(x,y,dim)
#测试代码,根据当前的x,预测其类别;
def predict(x,w1,w2,b1,b2):
alpha = np.dot(x, w1) #隐层输入
b=sigmoid(alpha-b1)#隐层输出
beta=np.dot(b,w2) #输出层输入
predictY=sigmoid(beta-b2) #神经网络输出
return predictY
print(predict(x,w1,w2,b1,b2))
三.课本5.13公式的推导
